概率论

1.概率的基本概念
确定性现象：在一定的条件下必然发生的现象，如同性电荷相互排斥；
统计规律性：在大量重复实验或者观察中所呈现出的固有规律性，如多次抛一枚硬币正面朝上大约有一半；
随机现象：在个别的实验中其结果呈现出不确定性，在大量的重复实验中又具有统计规律性的现象
2.条件概率
条件概率是概率中重要而实用的概念。所考虑的是事件A已发生的条件下事件B发生的概率。
设A，B是两事件，且 P(A)>0 ,称

P(B|A)=P(AB)P(A)

为在事件A发生的条件下事件B发生的条件概率。
不难验证，条件概率 P(.|A) 符合概率定义中的三个条件：
1. 对于每一事件B，有 P(B|A)⩾0 ；
2. P(S|A)=1 ；
3. 设B 是两两不相容的事件，则有 ，
既然条件概率符合上述的三个条件，故有对于任意事件 有

2.1随机变量
设随机试验的样本空间为 是定义在样本空间S上的实值单值函数，称 为D随机变量。

2.2离散型随机变量及其分布律

有一些随机变量，它的全部可能的取值是有限个或者可能是无限多个，这种随机变量称为离散型随机变量。
要掌握一个离散型随机变量X的统计规律，必须且只需要知道X的所有可能取值及取每一个可能值的概率。
设离散型随机变量X所有可能的取值为 xk(k=1,2,..) ，X取各个可能值的概率，即事情 {X=xk} 的概率为 P{X=xk}=pk,k=1,2,.. ： 称此式为离散型随机变量X的分布律，分布律也可以使用表格的方式表示：

X	x1	x2	...	xn	...
pk	p1	p2	...	pn	...

2.3.随机变量的分布函数：

【定义】设X是一个随机变量， x 是任意实数，函数：

F(x)=P{X<=x}

称为 X 的分布函数
对于任意的实数 x1 ， x2 ( x1<x2 )有:

P(x1<X<=x2)=P{X<=x2}−P{X<=x1}=F(x2)−F(x1)

因此，若已知X的分布函数，我们就可以知道X落在任意一区间 (x1,x2] 的概率 ，从这个意义上说，分布函数完整地描述了随机变量的统计规律性。
意义:如果将 看成是数轴上的随机点的坐标，那么，分布函数 F(x) 在 X 处的函数值就表示 落在区间 (−∞,x] 上的概率。
性质：
1） 是一个不减函数，
对于任意实数 有
2)

2.4.连续性随机变量和概率密度：

如果随机变量 X 的分布函数 F(x) ，存在非负函数 f(x) ，使得对于任意实数 x 有:

F(x)=∫x∞f(t)dt

则称 X 为连续型随机变量，其中函数 f(x) 称为 X 的概率密度函数，简称概率密度
性质：
1）连续型随机变量的分布函数是连续函数;
2) f(x)>=0 ;
3) ∫∞∞f(x)dx=1
4) 对于任意的实数 x1 ， x2 ( x1<x2 )有:

P(x1<X<=x2)==F(x2)−F(x1)=∫x2x1f(x)dx

5)若 f(x) 在点 x 处连续，则 F′(x)=f(x)

正态分布：

若连续随机变量 X 的概率密度函数是

f(x)=12π−−√σe−(x−u)22σ2

其中 u,σ(σ>0) 是常数，分别叫做均值和标准差，则称 X 服从参数为 u , σ 的正态分布或高斯分布，记为 X N(u,σ) ，它具有如下的性质：


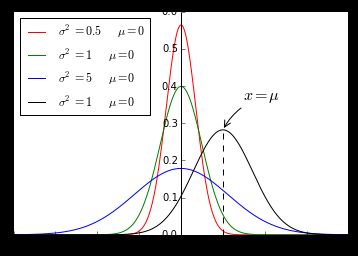
性质1：曲线为钟型，中间高，两头低，曲线下的面积为1，即分布函数 F(x)=P{−∞<X<∞}=∫∞−∞f(x)dx=1
性质2：曲线关于 x=u 对称，这表明对于任意的 h>0 有

P{u−h<X<=u}=P{u<X<=u+h}

如果固定 σ ，改变 u 的值，则图形沿Ox轴平移，而不改变其形状，可见正态分布的概率密度曲线 的位置完全由参数 所确定， 称为位置参数,即均值 u 决定曲线的位置。
性质3：当 x=u 时取到最大值 f(u)=12π√σ
x离 u 越远， f(x) 的值越小。这表明对于同样长度的区间，当区间离 u 越远，X落在这个区间上的概率越小。
性质4：在 x=u±σ 处曲线有拐点。曲线以Ox轴为渐近线。
如果固定 u ，改变 σ ，由于最大值 f(u)=12π√σ ，可知当 σ 越小时图像变得越尖，因而X落在 附近的概率越大，即 σ 标准方差决定曲线的形状，该值越大，数据越分散，曲线越“矮胖”。

随机变量的特征

1、数学期望

设离散随机变量X的分布律为：

P(X=xk)=pk,k=1,2,⋯

若级数 ∑k=1∞xkpk 绝对收敛，则称级数 ∑k=1∞xkpk 为随机变量X的数学期望，记为 E(X) ，即

E(X)=∑k=1∞xkpk

设连续型随机变量X的概率密度为 f(x) ，若积分 ∫∞−∞xf(x)dx 绝对收敛，则称积分 ∫∞−∞xf(x)dx 的值为随机变量X的数学期望，记为 E(X) ，即：

E(X)=∫∞−∞xf(x)dx

数学期望简称期望，又称为均值。
【举例】：某医院当新生儿诞生时，医生要根据婴儿的皮肤颜色、肌肉反弹、反应的敏感性、心脏的搏动等方面的情况作出评分，新生儿的得分X是一个随机变量，据以往的资料表明X的分布律为：

X	0	1	2	3	4	5	6	7	8	9	10
pk	0.002	0.001	0.002	0.005	0.002	0.04	0.18	0.37	0.25	0.12	0.01

试求X的数学期望 E(X) ；
解：

E(X)=0×0.02+1×0.01+2×0.02+3×0.05+4×0.02+5×0.04+6×0.18+7×0.37+8×0.25+9×0.12+10×0.01=7.15

意味着每一个新生儿的得分平均得分是7.15分；
性质1：设C是一个常数，则有 E(C)=C
性质2：设 X 是一个随机变量， C 是一个常数，则有 E(CX)=CE(X) ：
性质3：设 X,Y 是两个随机变量，则有 E(X+Y)=E(X)+E(Y) ，
这一性质可以推广到任意有限个随机变量之和的情况；
性质4：设 X,Y 是相互对立的随机变量，则有 E(XY)=E(X)E(Y)
这一性质可以推广到任意有限个相互独立随机变量之积的情况；

2.方差

设X是一个随机变量，若 E{[X−E(X)]2} 存在，则称 E{[X−E(X)]2} 为X的方差，记为 D(X) 或 Var(X) ，记 D(X)=E{[X−E(X)]2}
在应用上还引入量 D(X)−−−−−√ ，记为 σ ，称为标准差或者均方差。
按照定义，随机变量X的方差表达了X的取值与数学期望的偏离程度，若 D(X) 较小意味着X的取值比较集中在 E(X) 附近，反之，若 D(X) 较大则表示X的取值较分散，因此， D(X) 是刻画X取值分散程度的一个量，它是衡量X取值分散程度的一个尺度。
表达式可以写成下列形式：

D(X)=E(X2)−[E(X)]2

【性质】
1.设C是常数，则 D(C)=0 ；
2.设X是随机变量，C是常数，则有 D(CX)=C2D(X),D(X+C)=D(X) ： ，
3.设X,Y是随机变量，则有 D(X+Y)=D(X)+D(Y)+2E{(X−E(X))(Y−E(Y))} ：
特比的，如果X,Y相互独立，则有 D(X+Y)=D(X)+D(Y) ：
4. D(X)=0 的充要条件是X以概率1取常数 E(X) 即：P{X=E(X)}=1

3.协方差及相关系数

量 E{(X−E(X))(Y−E(Y))} 称为随机变量X和Y的协方差，记为 Cov(X,Y) ,即：

Cov(X,Y)=E{(X−E(X))(Y−E(Y))}

而

ρ=Cov(X,Y)D(X)−−−−−√D(Y)−−−−−√

称为随机变量X与Y的相关系数。
ρ=0 称X和Y不相关
由定义可知：
性质1： Cov(X,Y)=Cov(Y,X),C(X,X)=D(X)
性质2： D(X+Y)=D(X)+D(Y)+2Cov(X,Y)
性质3： Cov(X,Y)=E(XY)−E(X)E(Y)

4.直方图与箱线图

背景：
为了研究总体分布的性质，人们通过实验得到许多观测值，一般来说这些数据是杂乱无章的，为了利用它们进行统计分析，将这些数据加以整理，借助于表格或者图形它们加以描述，来观察其分布的规律：
直方图：
例子：
下面列出84个伊特拉斯坎（Etruscan）人男子的头颅的最大宽度（mm），来观察其数据分布的特征：

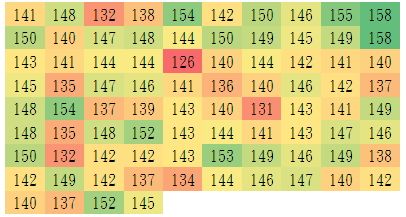
解：
从上述数据中可以得到：
最大值=158，最小值=126，平均值为143.7，总和为：12077，个数 n=84 ： ；
分割区间，统计频数与频率：
取区间[124.5,159.5]使得它能覆盖区间[126,158],将区间[124.5,159.5]等分为7个小区间，小区间的长度记为 Δ ： ，组距 Δ=(159.5−124.5)/7=5 ， ，小区间的端点称为组限，数据落在每个小区间内的个数叫做频数 fi ，频率为频数除以总个数 fi/n ，则得到数据的频数与频率如下：

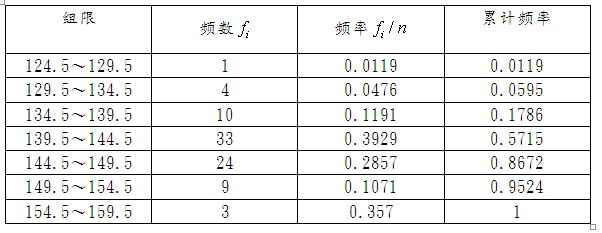
绘制频率直方图：
以组距为横坐标，以 fin/Δ 为高作为纵坐标，绘制的图形叫做频率直方图；

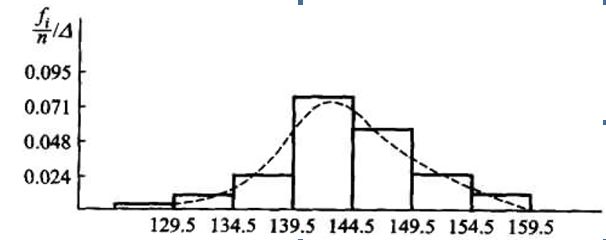
1.从图中可以看出，小矩形的面积的等于数据落在该小区间的频率 fin ；
2.由于当n很大的时候，频率接近于概率，因而，每一个小区间上的小矩形的面积接近于概率密度曲线下该小区间之上的曲边梯形的面积；
3.一般情况下，直方图的外廓曲线接近于总体X的概率密度曲线，如本例，它有一个峰值，中间高，两边低，类似于正太分布曲线；
4.从图中可以看出51.2%的人的最大头颅的宽度落在区间（134.5,144.5）之间。

5.距

定义：设X和Y是随机变量，
若： E(Xk),k=1,2,... 存在，称它为X的k阶原点距，简称k阶距；
若 E{[X−E(X)]k},k=2,3,... 存在，称它为X的k阶中心距。
若 E(XkYl),k,l=1,2,... 存在，称它为X和Y的k+l阶混合距
若 E{[X−E(X)]k[Y−E(Y)]l},k,l=1,2,...
存在，称它为X和Y的k+l阶混合中心距
显然，X的数学期望E（X）是X的一阶原点距，方差D(X)是X的二阶中心距，协方差 是 Cov(X,Y) 的二阶混合中心距
直观上来看，协方差表示的是两个变量总体误差的期望。
如果两个变量的变化趋势一致，也就是说如果其中一个大于自身的期望值时另外一个也大于自身的期望值，那么两个变量之间的协方差就是正值；如果两个变量的变化趋势相反，即其中一个变量大于自身的期望值时另外一个却小于自身的期望值，那么两个变量之间的协方差就是负值

5.距

参数的点估计问题：
设总体X的分布函数的形式已知，但它的一个参数或者多个参数未知，借助于总体X的一个样本来估计总体未知参数的值的问题称为参数的点的估计问题；
点估计的方法：
设总体X的分布函数 F(x,θ) 的形式为已知， θ 是带估计参数。 X1,X2,...Xn 是X的一个样本， x1,x2,...xn 是相应的一个样本值。点估计问题就是要构造一个适当的统计量 θ^(X1,X2,...Xn) ，它的观察值 θ^(x1,x2,...xn) 作为未知参数 θ 的近似值。我们称 θ^(X1,X2,...Xn) 为 θ 的估计量，称 θ^(x1,x2,...xn) 为 θ 的估计值。

最大似然估计法：
若总体X属于离散，其分布律 P(X=x)=p(x;θ),θ∈Θ 的形式为已知， θ 为待估计参数， Θ 是 θ 可能取值的范围。
设 X1,X2,...Xn 是来自X的样本，则 X1,X2,...Xn 的联合分布律为：

∏i=1np(xi,θ)

又设 x1,x2,...xn 是相应样本 X1,X2,...Xn 的一个样本值，易知样本 X1,X2,...Xn 取到观察值 x1,x2,...xn 的概率。
亦即事件 {X1=x1,X2=x2,...Xn=xn} 发生的概率为 ：

L(θ)=L(x1,x2,...,xn;θ)=∏i=1np(xi,θ),θ∈Θ

这一概率随 θ 的取值而变化，它是 θ 的函数， L(θ) 称为样本的 似然函数（注意，这里 x1,x2,...xn 是已知的样本值，它们都是常数）
由费希尔(R.A.Fisher)引入的极大似然估计法，就是固定样本观察值 x1,x2,...xn ，在 θ 取值的可能范围 Θ 内挑选使概率 L(x1,x2,...,xn;θ) 达到最大的参数值 θ^ ,作为参数 θ 的估计值。
即取 θ^ 使：

L(x1,x2,...,xn;θ^)=maxθ∈ΘL(x1,x2,...,xn;θ)

这样得到的 θ^ 与样本值 x1,x2,...xn 有关，常记为 θ^(x1,x2,...xn) ，称为参数 θ 的 极大似然估计值，而相应的统计量 θ^(X1,X2,...Xn) 称为参数 θ 的 极大似然估计量。

若总体X属于连续型，其密度函数 f(x;θ),θ∈Θ 的形式已知， θ 为待估参数， Θ 是 θ 可能取值的范围，设 X1,X2,...Xn 是来自X的样本，则 的联合密度为：

∏i=1nf(xi;θ)

设 x1,x2,...xn 是相应于样本 X1,X2,...Xn 的一个样本值，则随机点 (X1,X2,...Xn) 落在 (x1,x2,...xn) 的邻域（边长分别为 dx1,dx2,...,dxn 的n维立方体）内的概率近似的为：

∏i=1nf(xi;θ)dxi

其值随 θ 的取值而变化。与离散的情况一样，我们取 θ 的估计值 θ^ 使上述概率取得最大值，但因子 ∏ni=1dxi 不随 θ 而改变，故只需考虑函数

L(θ)=L(x1,x2,...,xn;θ)=∏i=1nf(xi;θ)

的最大值，这里 L(θ) 称为样本的似然函数。若：

L(x1,x2,...,xn;θ^)=maxθ∈ΘL(x1,x2,...,xn;θ)

则称 θ^(x1,x2,...xn) ，称为参数 θ 的 极大似然估计值，而称 θ^(X1,X2,...Xn) 为参数 θ 的 极大似然估计量。
在很多情形， p(x;θ) 和 f(x;θ) 关于 θ 可微，这时 θ 可以从方程：

ddθL(θ)=0

解得。由因 L(θ) 与 lnL(θ) 在同一 θ 处取到极值，因此， θ 的极大似然估计也可以从方程：

ddθlnL(θ)=0

求得，这一方程求解往往比较方便。