图像修复：Object Removal by Exemplar-Based Inpainting 学习笔记

Overview

这是一篇比较经典的exemplar-based的inpainting算法，算法思路比较简单，是一种贪心算法，主要分为以下几步：

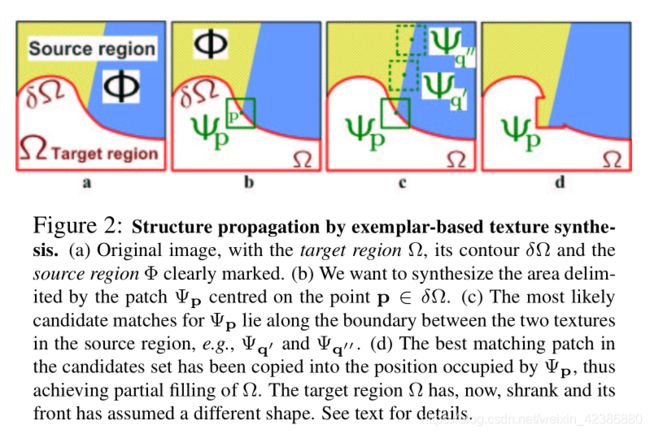
1、在需要填充区域的轮廓上计算权重，选择权重最大的轮廓点作为待填充点

2、在该点周围领域取一个一定大小的patch块，在图像其他区域内找该patch快的最近邻patch

3、将最近邻patch块对应到需要填充区域的部分复制到等待填充的区域，再重复上述步骤，直至所有点都填充完毕。

从上述算法流程来看，算法比较简单，是一个基于填充区域轮廓优先级的算法，算法是一个贪心算法。存在的一个明显弊端就是无法保证最终整体填充效果。

Impletion Detail

1. filling order

paper中着重讲述了填充顺序的关键性，也是本片paper的主要创新点，轮廓点上的优先级由两部分组成，其中C（p）是confidence term, D§是data term.
$$P(p)=C(p)D(p)$$
1、confidence term： 表明该点的可靠度

2、data term: 根据patch周围数据进行计算的项

1.1 confidence term

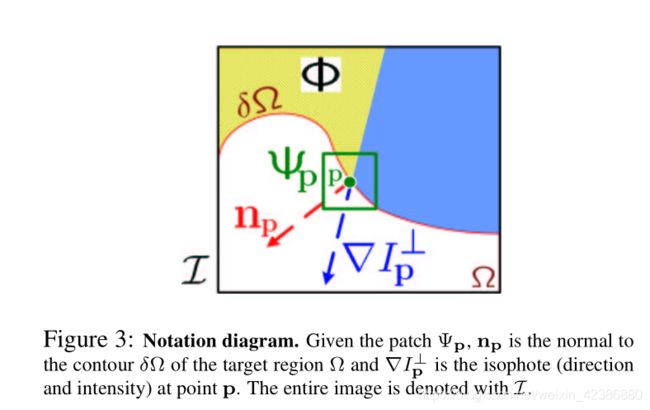
condidence 项可视为围绕在点$p$周围点的可信度，目的是优先填充那些周围有更多已知点的patch快。

其计算公式如下,${\Psi }_p$表示以$p$点为中心的patch快，其中$|{\Psi }_p|$ 是整个patch的面积，
$$C(p)=\frac{{\sum }_{q\in {\Psi }_p}C(q)}{|{\Psi }_p|}$$

1.2 data term

数据项的目的是优先填充有较强纹路结构的点，其计算方式如下
$$D(p)=\frac{|▽I_p^{\perp }\cdot n_p|}{\alpha }$$
其意义如下图，在点$p$处获得待填充轮廓的法线方向$n_p$, $▽I_p^{\perp }$ 则表示其梯度方向旋转90度，从而可以找到具有比较强结构特征的点。从该项可以看出那些梯度方向和轮廓垂直，且梯度比较大的点，拥有更高的优先级。

propagate texture and structure information

在找到优先级最高的点后，以$p$为中心的patch块${\Psi }_p$, 在已知图像区域中寻找一个相似的最高的patch块${\Psi }_{\hat{q}}$。

Updating confidence values

使用${\Psi }_{\hat{q}}$ 填充${\Psi }_{\hat{p}}$后，confidence的值也需要进行更新，对于新填充的点，统一使用点$\hat{p}$处的confidence值进行填充。
$$C(q)=C(\hat{p}),$$
更新confidence从而可以动态的评估边界上各个patch块的相对优先级，而不需要和图像相关的参数。随着填充的进行，confidence值会不断减少，表明我们对于目标中心区域的像素点更不确定。

review of the algorithm

下表为整个算法的流程，正如先前所说，该算法是一个贪心算法，每次寻找边界上的一个最优点进行patch块的生长，直到所有点都被填充。

缺点

1. 基于样例算法的共有缺陷：无法应对没有合适填充样例的图片
2. 无法保证最终填充图像整体的consistence.

some improvement method

filling order

填充次序对于该算法来说至关重要，是该算法能work的重要条件.也有一些对于填充顺序进行改良的算法，如下一个是基于样例稀疏性的。

本算法中data term 是利用轮廓的法线方向和梯度垂直向量的点积作为其数据项，[1]的算法则使用了patch块的稀疏性作为度量，提出优先填充稀疏性更高的patch块，从而改善一些情况下填充的效果。

Result

其算法实际运行图例如下面gif所示，对于需要填充的建筑物，沿着其轮廓线寻找优先级高的点，依次不断填充，最终获得了不错的一个效果。

对于图像中有较多可以copy的patch块的场景，修复效果都还不错，但是无法保证最终整体填充效果，容易出现到最后怎么找patch块都会出现不连续的问题，所以后来大牛们又提出了很多基于全局优化的inpainting/Image completion算法。