RDD、矩阵基础——3. 矩阵、向量(Breeze、BLAS)
MLlib库底层的Vector(向量)、Matrix(矩阵)运算使用了
Breeze库和BLAS库。
Breeze库提供了相应计算的接口(Linalg)。
但是在MLlib里面同时也提供了Vector和Linalg等的实现。
BLAS(线性代数运算库)广泛应用于高性能计算领域。
一、Breeze库
导入:
import breeze.linalg._ import breeze.numerics._
1. Breeze创建矩阵、向量
| 操作名称 |
Breeze函数 |
输出结果 |
对应Numpy函数 |
| 全0矩阵 |
DenseMatrix.zeros[Double](2,3) |
0.0 0.0 0.0 0.0 0.0 0.0 |
zeros((2,3)) |
| 全0向量 |
DenseVector.zeros[Double](3) |
DenseVector(0.0,0.0,0.0) |
zeros(3) |
| 全1向量 |
DenseVector.ones[Double](3) |
DenseVector(1.0,1.0,1.0) |
ones(3) |
| 按数值填充向量 |
DenseVector.fill(3){5.0} |
DenseVector(5.0,5.0,5.0) |
ones(3)*5.0 |
| 生成随机向量 |
DenseVector.range(start,stop,step), 或Vector.rangeD(start,end,step) |
|
|
| 线性等分向量(用于产生start, stop之间的N点行向量) |
DenseVector.linspace(start,stop,numvals) |
|
|
| 单位矩阵 |
DenseMatr.eye[Double](3) |
1.0 0.0 0.0 0.0 1.0 0.0 0.0 0.0 1.0 |
eye(3) |
| 对角矩阵 |
diag(DenseVector(1.0,2.0,3.0)) |
1.0 0.0 0.0 0.0 2.0 0.0 0.0 0.0 3.0 |
diag((1.0,2.0,3.0)) |
| 按照行创建矩阵 |
DenseMatrix((1.0,2.0),(3.0,4.0)) |
1.0 2.0 3.0 4.0 |
array([[1.0,2.0],[3.0,4.0]]) |
| 按照行创建向量 |
DenseVector(1,2,3,4) |
[1 2 3 4] |
array([1,2,3,4]) |
| 向量转置 |
DenseVector(1,2,3,4).t |
[1 2 3 4]T |
array([1 2 3 4]).reshape(-1,1) |
| 从函数创建向量 |
DenseVector.tabulate(3){i => i*2} |
[0 1 4] |
|
| 从函数创建矩阵 |
DenseMatrix.tabulate(3,2){case(i,j) => i+j} |
0 1 1 2 2 3 |
|
| 从数组创建向量 |
new DenseVector(array(1, 2, 3,4)) |
[1 2 3 4] |
|
| 从数组创建矩阵 |
new DenseMatrix(2,3,array(11,12,13,21.22,23)) |
11 12 13 21 22 23 |
|
| 0到1的随机向量 |
DenseVector.rand(4) |
[0.0222 0.2231 0.5356 0.6902] |
|
| 0到1的随机矩阵 |
DenseMatrix.rand(2,3) |
0.2122 0.3033 0.8675 0.6628 0.0023 0.9987 |
|
实例:
val v1 = DenseVector(1.0,2.0,3.0)
val v2 = DenseVector(Array(1,2,3,4))
val v3 = DenseVector.rand(4)
val m1 = DenseMatrix((1.0,2.0),(3.0,4.0))
m1.t
val m2 = new DenseMatrix(2, 3, Array(1,2,3,4,5,6))
val m3 = DenseMatrix.rand(2,3)
val m4 = DenseMatrix.tabulate(2,3){case (i,j) => i+j}
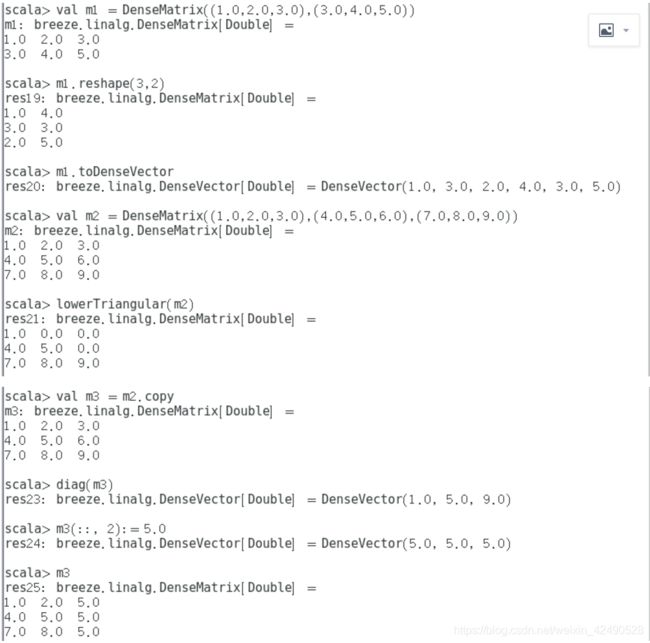
2. Breeze取数据及数据操作
2.1 Breeze取数据
| 操作名称 |
Breeze函数 |
对应Numpy函数 |
| 指定位置 |
a(0,1) |
a[0,1] |
| 向量子集 |
a(1 to 4), a(1 until 5), a.slice(1,5) |
a[1:5] |
| 按照指定步长取子集 |
a(5 to 0 by -1) |
a[5:0:-1] |
| 指定开始位置至结尾 |
a(1 to -1) |
a[1:] |
| 最后一个元素 |
a(-1) |
a[-1] |
| 矩阵指定列 |
a(::, 2) |
a[:,2] |
实例:
2.2 Breeze数据操作
| 操作名称 |
Breeze函数 |
对应Numpy函数 |
| 调整矩阵形状 |
a.reshape(3,2) |
a.reshape(3,2) |
| 矩阵转成向量 |
a.toDenseVector(Makes copy) |
a.flatten() |
| 复制下三角 |
lowerTriangular(a) |
tril(a) |
| 复制上三角 |
upperTriangular(a) |
triu(a) |
| 矩阵复制 |
a.copy |
np.copy(a) |
| 取对角线元素 |
diag(a) |
diagonal(a) |
| 子集赋数值 |
a(1 to 4) := 5.0 |
a[1:4]=5.0 |
| 子集赋向量 |
a(1 to 4) := DenseVector(1.0,2.0,3.0) |
a[1:4]=[1.0 2.0 3.0] |
| 矩阵赋值 |
a(1 to 3, 1 to 3) := 5.0 |
a[2:4, 2:4] = 5.0 |
| 矩阵列赋值 |
a(::, 2) := 5.0 |
a(:,3) = 5 |
| 垂直连接矩阵 |
DenseMatrix.vertcat(a,b) |
[a;b] |
| 横向连接矩阵 |
DenseMatrix.horzcat(a,b) |
[a,b] |
| 向量连接 |
DenseVector.vertcat(a,b) |
[a b] |
实例:
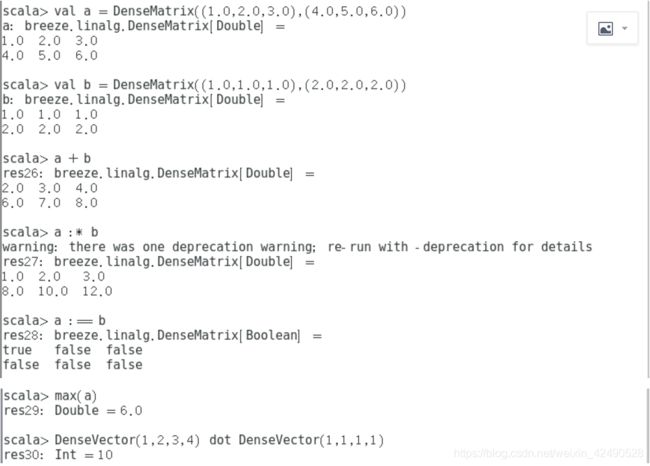
3. Breeze数值计算函数
| 操作名称 |
Breeze函数 |
对应Numpy函数 |
| 元素加法 |
a + b |
a + b |
| 元素乘法 |
a :* b |
a * b |
| 元素除法 |
a :/ b |
a / b |
| 元素比较 |
a :< b |
a < b |
| 元素相等 |
a :== b |
a == b |
| 元素追加 |
a :+= 1.0 |
a += 1 |
| 元素追乘 |
a :*= 2.0 |
a *= 2 |
| 向量点积 |
a dot b, a.t * bT |
dot(a,b) |
| 元素最大值 |
max(a) |
a.max() |
| 元素最大值及位置 |
argmax(a) |
a.argmax() |
实例:
4. Breeze求和函数
| 操作名称 |
Breeze函数 |
对应Numpy函数 |
| 元素求和 |
sum(a) |
a.sum() |
| 每一列求和 |
sum(a, Axis._0), 或sum(a(::,*)) |
sum(a,0) |
| 每一行求和 |
sum(a,Axis._1), 或sum(a(*, ::)) |
sum(a,1) |
| 对角线元素和 |
trace(a) |
a.trace() |
| 累积和 |
accumulate(a) |
a.cumsum() |
实例:
5. Breeze布尔函数
| 操作名称 |
Breeze函数 |
对应Numpy函数 |
| 元素与操作 |
a :& b |
a & b |
| 元素或操作 |
a :| b |
a | b |
| 元素非操作 |
!a |
~a |
| 任意元素非零 |
any(a) |
any(a) |
| 所有元素非零 |
all(a) |
all(a) |
针对布尔类型的,不常用
6. Breeze线性代数函数
| 操作名称 |
Breeze函数 |
对应Numpy函数 |
| 线性求解 |
a \ b |
linalg.solve(a,b) |
| 转置 |
a.t |
a.conj.transpose() |
| 求特征值 |
det(a) |
linalg.det(a) |
| 求逆 |
inv(a) |
linalg.inv(a) |
| 求伪逆 |
pinv(a) |
linalg.pinv(a) |
| 求范数 |
norm(a) |
norm(a) |
| 特征值和特征向量 |
eigSym(a) |
linalg.eig(a)[0] |
| 特征值 |
val(er,ei,_) = eig(a)(实部与虚部分开) |
lialg.eig(a)[0] |
| 特征向量 |
eig(a)._3 |
|
| 奇异值分解 |
val svd.SVD(u,s,v) = svd(a) |
linalg.svd(a) |
| 求矩阵的秩 |
rank(a) |
rank(a) |
| 矩阵长度 |
a.length |
a.size |
| 矩阵行数 |
a.rows |
a.shape[0] |
| 矩阵列数 |
a.cols |
a.shape[1] |
实例:
7. Breeze取整函数
| 操作名称 |
Breeze函数 |
对应Numpy函数 |
| 四舍五入 |
round(a) |
around(a) |
| 小于的最小整数 |
ceil(a) |
ceil(a) |
| 大于的最大整数 |
floor(a) |
floor(a) |
| 符号函数 (1.0为正,-1.0为负) |
signum(a) |
sign(a) |
| 取正数 |
abs(a) |
abs(a) |
实例:
8. Breeze其他函数
常量函数、复数函数、三角函数、对数和指数函数等不常用。
(详见SPARK MLLIB机器学习)
二、BLAS库
BLAS(线性代数运算库)广泛应用于高性能计算领域。
BLAS按照功能可以分为3类:
Level 1:向量-向量运算
如:点积(ddot)、加法和数乘(daxpy)、绝对值的和(dasum)等
Level 2:矩阵-向量运算
主要函数是矩阵和向量的乘法(dgemv)
Level 3:矩阵-矩阵运算
主要函数是矩阵的乘法(dgemm)
每种运算都区分不同的数据类型(单精度、多精度、复数、双精度复数),
如矩阵乘法分为:sgemm(单精度)、dsymm(多精度)、zhemm(双精度复数)。
之所以分这么多种,是针对不同类型的矩阵都设计专门的算法,是的计算性能最优。
BLAS基本函数
| 函数 |
名称 |
| 点积 |
dot |
| 常数乘以向量加 另一个向量 |
axpy |
| 准备Givens旋转 |
rotg |
| 实施旋转 |
rot |
| 准备修改过的 Givens旋转 |
rotmg |
| 实施修改过的 Givens旋转 |
gotm |
| 复制x到y |
copy |
| 交换x和y |
swap |
| 2-范数 (欧几里得长度) |
nrm2 |
| 绝对值求和 |
asum |
| 常数乘以向量 |
scal |
| 最大绝对值元素 的索引 |
amax |
| 其他 |
以单精度类型函数为例,以下为BLAS的基本函数。
1. BLAS向量-向量运算
| SROTG |
Givens旋转设置 |
| SROTMG |
改进Givens旋转设置 |
| SROT |
Givens旋转 |
| SROTM |
改进Givens旋转 |
| SSWAP |
交换x和y |
| SSCAL |
常数a乘以向量x() |
| SCOPY |
把x复制到y |
| SAXPY |
向量y+常数a乘以向量x(y = a*x + y) |
| SDOT |
点积 |
| SDSDOT |
扩展精度累积的点积 |
| SNRM2 |
欧氏范数 |
| SCNRM2 |
欧氏范数 |
| SASUM |
绝对值之和 |
| ISAMAX |
最大值位置 |
2. BLAS矩阵-向量运算
| SGEMV |
矩阵向量乘法 |
| SGBMV |
带状矩阵向量乘法 |
| SSYMV |
对称矩阵向量乘法 |
| SSBMV |
对称带状矩阵向量乘法 |
| SSPMV |
对称填充矩阵向量乘法 |
| STRMV |
三角矩阵向量乘法 |
| STBMV |
三角带状矩阵向量乘法 |
| STPMV |
三角填充矩阵向量乘法 |
| STRSV |
求解三角矩阵 |
| STBSV |
求解三角带状矩阵 |
| STPSV |
求解三角填充矩阵 |
| SGER |
A := alpha*x*y’ + A |
| SSYR |
A := alpha*x*x’ + A |
| SSPR |
A := alpha*x*x’ + A |
| SSYR2 |
A := alpha*x*y’ + alpha*y*x’ + A |
| SSPR2 |
A := alpha*x*y’ + alpha*y*x’ + A |
3. BLAS矩阵-矩阵运算
| SGEMM |
矩阵乘法 |
| SSYMM |
对称矩阵乘法 |
| SSYPK |
对称矩阵的秩-k修正 |
| SSYR2K |
对称矩阵的秩-2k修正 |
| STRMM |
三角矩阵乘法 |
| STRSM |
多重右端的三角线性方程组求解 |
向量与向量
加:+ 减:- 点乘: :* 点除::/ 向量乘法: * 向量除法: /
矩阵与矩阵
加:+ 减:- 点乘: :* 点除::/ 矩阵乘法: * 矩阵除法: /
矩阵或向量与数值
加:+ 减:- 乘:* 除:/
矩阵和向量
加:+ 减:- 点乘: :* 点除::/ 矩阵乘法: * 矩阵除法: /
Matrix(*, ::)+Vector 逐行
Matrix(::, *)+Vector 逐列