论文阅读：Recipe for a General, Powerful, Scalable Graph Transformer

Graph Transformer)

论文和代码地址

论文地址：https://arxiv.org/pdf/2205.12454v4
代码地址：https://github.com/rampasek/GraphGPS

1 介绍与贡献

Graph Transformers（GTs）通过允许节点对图中所有其他节点进行注意（全局注意力），从而缓解了与稀疏消息传递机制相关的基本限制。但存在以下问题：

• 由于图结构不像图像一样有着标准化的位置关系，因此全局注意力位置编码要求比较高
• 标准的全局注意力会导致图中有 $N$ 个节点和 $E$ 条边时的二次计算开销 $O(N^2)$，这使得GTs仅限于处理最多几百个节点的小型图。

在本文中，提出了一种构建通用、强大且可扩展的图变换器（GPS）的方案。该方案的模块如下：

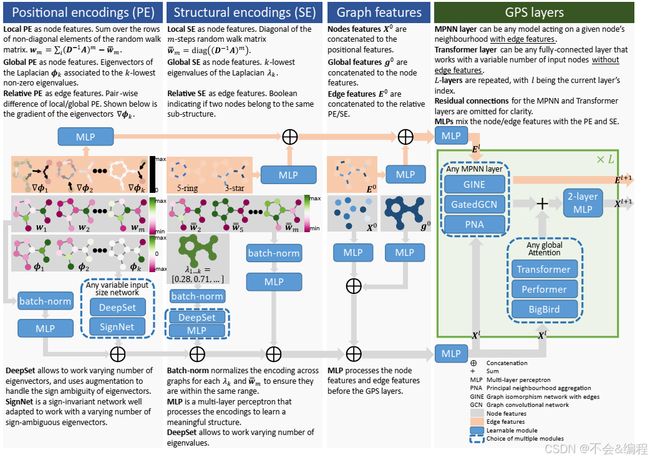
• embedding模块：负责将位置编码（position encoding，PE）和结构编码（structure encoding，SE）与节点、边和图级输入特征聚合。
• processing模块：局部消息传递和全局注意力层组合的处理模块。

embedding模块将多个提出的PE和SE方案嵌入到local和global级别，作为附加节点特征；同时位置和结构的相对特征融入边特征

processing模块定义了一个计算图，计算图在消息传递图神经网络（MPNNs）和Transformer的全局注意力之间保持了平衡。

论文的贡献如下：

1. 提供了一个通用、强大、规模可变的Graph Transformer构建方案。
2. 提供了PE和SE的更好定义，并将其归为local、global、relative三类。
3. 证明了GPS使用linear global attention可以扩展到大规模图
4. 证明了方法的有效性

2 GPS模型

2.1 模型框架图

2.2 PE和SE

位置编码（PE）：旨在提供图中给定节点在空间中的位置概念。因此，当两个节点在图或子图中彼此接近时，它们的PE也应该接近。

结构编码（SE）：旨在提供图或子图结构的嵌入，以帮助提高图神经网络（GNN）的表达能力和泛化能力。因此，当两个节点共享相似的子图，或者当两个图相似时，它们的SE也应该接近。

PE、SE方案，它们基本都可以归纳到local、global、relative三种类别

PE方案

• Local PE（作为node features）

  • 功能：使节点能够了解其在局部集群中的位置。两个节点之间越接近，它们的局部PE（位置编码）越相似。例如，在一个句子中，两个词越接近，它们的局部PE也越相似。
  • 计算方式
    • 对 m 步随机游走矩阵中非对角线元素的每一列进行求和
    • 每个节点到其对应簇质心的距离

• global PE (作为node features)

  • 功能：使节点能够了解其在整个图中的位置。两个节点越接近，它们的全局PE越相似。
  • 计算方式
    • 邻接矩阵、拉普拉斯矩阵或距离矩阵的特征向量表示。
    • SignNet，它组合了relative PE和local SE。
    • 每个节点到图质心的距离。
    • 图中每个连接组件的唯一标识符。

• Relative PE （作为edge features）

  • 功能：使两个节点能够理解它们之间的距离或方向关系。
  • 计算方式
    • 基于最短路径、热核、随机游走、格林函数、图的测地线或任何local/global PE的节点对之间的距离。
    • 特征向量的梯度任何local/global PE。
    • 具有特定节点间距离的PEG层
    • 用布尔值来表示两个节点是否在一个簇中。

SE方案

• Local SE (作为node feature)

  • 功能：让每个节点知道它属于哪个子结构。给定半径为m的子图，两个节点周围的m跳子图越相似，它们的局部结构嵌入（SE）就越接近。
  • 计算方式
    • 节点的度。
    • m阶随机游走矩阵的对角线元素。
    • 热核对角线元素的时间导数。
    • 枚举或计数预定义结构，如三角形、环等。
    • Ricci曲率。

• Global SE (作为graph feature)

  • 功能：图的全局结构的信息描述。两个图越相似，它们的全局结构嵌入（SE）就越接近。
  • 计算方式
    • 邻接矩阵或者拉普拉斯矩阵的特征值。
    • 图的属性：直径、周长、节点数、边数、节点与边的比例等。

• Relative SE (作为edge feature)

  • 功能：让两个节点知道彼此的结构差异。边嵌入与任意局部结构嵌入（SE）之间的差异相关
  • 计算方式
    • 节点对的距离、编码或者任何local SE的梯度。
    • 用布尔值表示两个节点是否在一个子结构中。

2.3 GPS layer: 一种MPNN+Transformer的混合模型

防止早期平滑

在以前，通常在Transformer之前使用几个MPNN层。由于MPNN存在过度平滑、过度压缩和等问题，这些层可能无法在早期阶段保持一些信息。尽管它们可以利用PE/SE或更具表达力的MPNN，它们仍然可能会丢失信息。而GPS layer可以缓解这个问题，它的流程如下：

• 模块化的 GPS 层，结合了局部 MPNN 和全局注意力模块。
• 局部 MPNN 将真实的边特征编码到节点级别的隐藏表示中，
• 全局注意力机制可以隐式地利用这些信息以及 PE/SE 来推断两个节点之间的关系，即使没有显式的边特征。
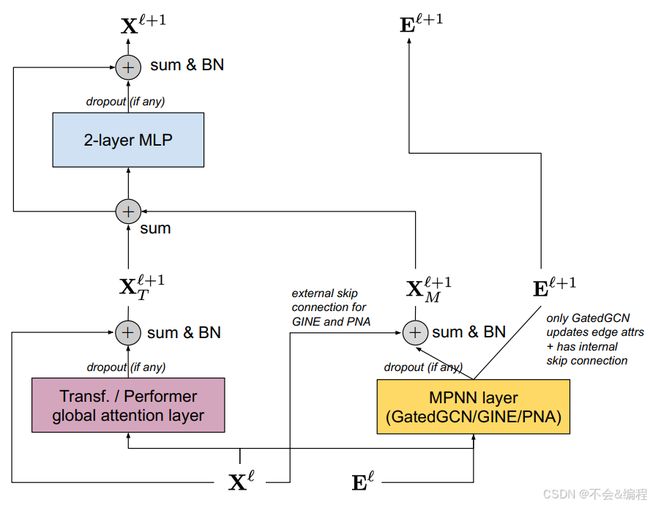
• 在每个功能模块（MPNN 层、全局注意力层、MLP）之后，我们应用残差连接，并接着批归一化（BN）。
• 在 2 层 MLP 中，我们使用 ReLU 激活函数，并且其内部隐藏层维度是输入特征维度 $d_{\ell }$ 的两倍。
• 注意，GPS 层作为一个整体的输入和输出维度是相同的。

方程如下：
$$\begin{array}{rlrl}{\mathbf{X}}^{\ell +1},{\mathbf{E}}^{\ell +1}& ={\mathrm{GPS}}^{\ell }\left({\mathbf{X}}^{\ell },{\mathbf{E}}^{\ell },\mathbf{A}\right)& & (1)\\ \text{computed as}{\mathbf{X}}_M^{\ell +1},{\mathbf{E}}^{\ell +1}& ={\mathrm{MPNN}}_e^{\ell }\left({\mathbf{X}}^{\ell },{\mathbf{E}}^{\ell },\mathbf{A}\right),& & (2)\\ {\mathbf{X}}_T^{\ell +1}& ={\text{GlobalAttn}}^{\ell }\left({\mathbf{X}}^{\ell }\right),& & (3)\\ {\mathbf{X}}^{\ell +1}& ={\mathrm{MLP}}^{\ell }\left({\mathbf{X}}_M^{\ell +1}+{\mathbf{X}}_T^{\ell +1}\right),& & (4)\end{array}$$

• $\mathbf{A}\in {\mathbb{R}}^{N\times N}$ 是一个图的邻接矩阵，其中包含 $N$ 个节点和 $E$ 条边；
• ${\mathbf{X}}^{\ell }\in {\mathbb{R}}^{N\times d_{\ell }}$ 和 ${\mathbf{E}}_{\alpha }^{\ell }\in {\mathbb{R}}^{E\times d_{\ell }}$ 分别是 $d_{\ell }$ 维的节点特征和边特征；
• MPNN${}_e^{\ell }$ 和 GlobalAttn${}^{\ell }$ 分别是带边特征的MPNN和全局注意力机制在第 $\ell$ 层的实例，它们具有相应的可学习参数；
• MLP${}^{\ell }$ 是一个两层的MLP块。

模块化（Modularity） 使得各个模块或组件可以互相替换、灵活组合，从而方便调整或扩展。

1. 初始 PE/SE 类型：在系统中，可以根据需要替换不同类型的节点特征（PE）和边特征（SE）。

2. 处理这些 PE/SE 的网络：例如，可以使用不同类型的神经网络来处理这些特征（如MLP），这部分也可以进行替换。

3. MPNN 和 GlobalAttn 层：它们是 模块化的，即它们可以被其他不同类型的图神经网络层或者注意力机制所替代，适应不同的需求。

4. 任务特定预测头：这是网络最后的输出层，用于根据任务的具体需求进行预测。任务特定的预测头也可以根据不同的任务进行更换。

GPS更详细的方程如下：
$$\begin{array}{rlr}{\mathbf{X}}^{\ell +1},{\mathbf{E}}^{\ell +1}& ={\mathrm{GPS}}^{\ell }\left({\mathbf{X}}^{\ell },{\mathbf{E}}^{\ell },\mathbf{A}\right)& \left(6\right)\\ \text{computed as}{\hat{\mathbf{X}}}_M^{\ell +1},{\mathbf{E}}^{\ell +1}& ={\mathrm{MPNN}}_e^{\ell }\left({\mathbf{X}}^{\ell },{\mathbf{E}}^{\ell },\mathbf{A}\right),& (7)\\ {\hat{\mathbf{X}}}_T^{\ell +1}& ={\text{GlobalAttn}}^{\ell }\left({\mathbf{X}}^{\ell }\right),& \left(8\right)\\ {\mathbf{X}}_M^{\ell +1}& =\mathrm{BatchNorm}\left(\mathrm{Dropout}\left({\hat{\mathbf{X}}}_M^{\ell +1}\right)+{\mathbf{X}}^{\ell }\right),& (9)\\ {\mathbf{X}}_T^{\ell +1}& =\mathrm{BatchNorm}\left(\mathrm{Dropout}\left({\hat{\mathbf{X}}}_T^{\ell +1}\right)+{\mathbf{X}}^{\ell }\right),& (10)\\ {\mathbf{X}}^{\ell +1}& ={\mathrm{MLP}}^{\ell }\left({\mathbf{X}}_M^{\ell +1}+{\mathbf{X}}_T^{\ell +1}\right)& (11)\end{array}$$

其算法框架如下：

• $⨁$ 表示一个操作符，用于将输入的节点或边特征与各自的位置信息和/或结构编码相结合，实际上这是一个连接操作符（concatenation operator），可以改为求和（sum）或其他操作符；
• NodeEncoder 和 EdgeEncoder 是针对特定数据集的初始节点和边特征编码器，可能包含可学习的参数，在框架图应该是MLP（我理解是这样）
• MPNN${}_e$ 和 GlobalAttn 在每一层 $\ell$ 上都有相应的可学习参数；${\hat{\mathbf{X}}}_M^{\ell +1}$ 和 ${\hat{\mathbf{X}}}_T^{\ell +1}$ 分别表示由局部消息传递模块和全局注意力模块给出的中间节点表示；
• MLP${}^{\stackrel{◯}{\ell }}$ 是一个多层感知机模块，具有自己的可学习参数，用于结合中间的 ${\mathbf{X}}_M^{\ell +1}$ 和 ${\mathbf{X}}_T^{\ell +1}$。

回顾一下框架图：