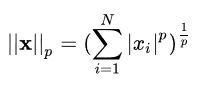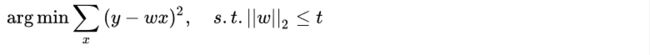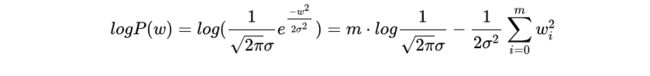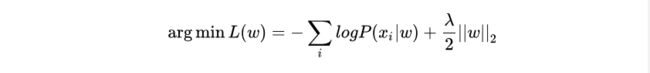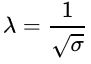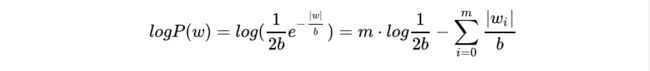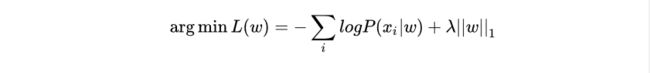范数的简单总结

引入：

函数与几何图形往往是有对应的关系，这个很好想象，特别是在三维以下的空间内，函数是几何图像的数学概括，而几何图像是函数的高度形象化，比如一个函数对应几何空间上若干点组成的图形。
但当函数与几何超出三维空间时，就难以获得较好的想象，于是就有了映射的概念，映射表达的就是一个集合通过某种关系转为另外一个集合。通常数学书是先说映射，然后再讨论函数，这是因为函数是映射的一个特例。
为了更好的在数学上表达这种映射关系，（这里特指线性关系）于是就引进了矩阵。这里的矩阵就是表征上述空间映射的线性关系。而通过向量来表示上述映射中所说的这个集合，而我们通常所说的基，就是这个集合的最一般关系。于是，我们可以这样理解，一个集合（向量），通过一种映射关系（矩阵），得到另外一个集合（另外一个向量）。
那么向量的范数，就是表示这个原有集合的大小。
而矩阵的范数，就是表示这个变化过程的大小的一个度量。

何为范数？

我们知道距离的定义是一个宽泛的概念，只要满足非负、自反、三角不等式就可以称之为距离。范数是一种强化了的距离概念，它在定义上比距离多了一条数乘的运算法则。有时候为了便于理解，我们可以把范数当作距离来理解。
在数学上，范数包括向量范数和矩阵范数，向量范数表征向量空间中向量的大小，矩阵范数表征矩阵引起变化的大小。一种非严密的解释就是，对应向量范数，向量空间中的向量都是有大小的，这个大小如何度量，就是用范数来度量的，不同的范数都可以来度量这个大小，就好比米和尺都可以来度量远近一样；对于矩阵范数，学过线性代数，我们知道，通过运算AX=B，可以将向量X变化为B，矩阵范数就是来度量这个变化大小的。

一.几种向量范数的定义和含义 ：

1、 L-P范数 ：

与闵可夫斯基距离的定义一样，L-P范数不是一个范数，而是一组范数，其定义如下：

表示向量元素绝对值的p次方和的1/p次幂，matlab调用函数norm(x, p)。

根据P 的变化，范数也有着不同的变化，一个经典的有关P范数的变化图如下：

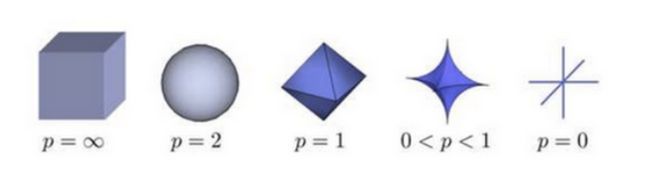
上图表示了p从无穷到0变化时，三维空间中到原点的距离（范数）为1的点构成的图形的变化情况。以常见的L-2范数（p=2）为例，此时的范数也即欧氏距离，空间中到原点的欧氏距离为1的点构成了一个球面。
实际上，在0时，Lp并不满足三角不等式的性质，也就不是严格意义下的范数。以p=0.5，二维坐标(1,4)、(4,1)、(1,9)为例：

因此这里的L-P范数只是一个概念上的宽泛说法。

2、 L0范数 ：

当P=0时，也就是L0范数，由上面可知，L0范数并不是一个真正的范数，它主要被用来度量向量中非零元素的个数。用上面的L-P定义可以得到的L-0的定义为：

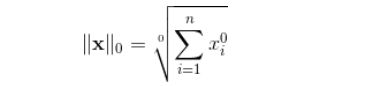
这里就有点问题了，我们知道非零元素的零次方为1，但零的零次方，非零数开零次方都是什么鬼，很不好说明L0的意义，所以在通常情况下，大家都用的是：

表示向量x中非零元素的个数。
对于L0范数，其优化问题为：

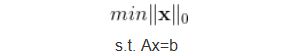
在实际应用中，由于L0范数本身不容易有一个好的数学表示形式，给出上面问题的形式化表示是一个很难的问题，故被人认为是一个NP-hard问题。所以在实际情况中，L0的最优问题会被放宽到L1或L2下的最优化。

3、 L1范数 ：

L1范数是我们经常见到的一种范数，它的定义如下：

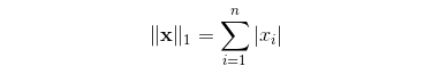
表示向量x中非零元素的绝对值之和，matlab调用函数norm(x, 1) 。
L1范数有很多的名字，例如我们熟悉的曼哈顿距离、最小绝对误差等。使用L1范数可以度量两个向量间的差异，如绝对误差和（Sum of Absolute Difference）：

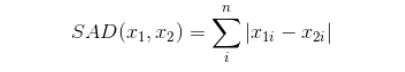
对于L1范数，它的优化问题如下：

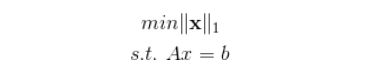
由于L1范数的天然性质，如果把L1范数作为目标函数进行优化，对L1优化的解是一个稀疏解，因此L1范数也被叫做稀疏规则算子。通过L1可以实现特征的稀疏，去掉一些没有信息的特征，例如在对用户的电影爱好做分类的时候，用户有100个特征，可能只有十几个特征是对分类有用的，大部分特征如身高体重等可能都是无用的，利用L1范数就可以过滤掉。

4、 L2范数 ：

L2范数是我们最常见最常用的范数了，我们用的最多的度量距离欧氏距离就是一种L2范数，它的定义如下：

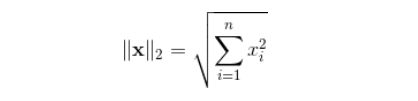
表示向量元素的平方和再开平方，matlab调用函数norm(x, 2)。
像L1范数一样，L2也可以度量两个向量间的差异，如平方差和（Sum of Squared Difference）/最小均方误差:

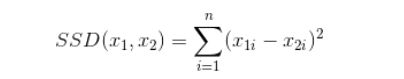
对于L2范数，它的优化问题如下：

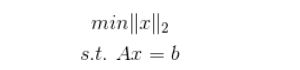
L2范数通常会被用来做优化目标函数的正则化项，防止模型为了迎合训练集而过于复杂造成过拟合的情况，从而提高模型的泛化能力。

5、 L∞范数 ：

当p = ∞时，也就是 L∞范数，它主要被用来度量向量元素的最大值，matlab调用函数norm(x, inf)。
与L0一样，通常情况下表示为 :

L∞范数又被称为 H∞,在鲁棒控制、滤波中作为一项优化指标。

最通俗的向量范数记法：
L0范数:向量中非零元素的个数。
L1范数:为绝对值之和。
L2范数:就是通常意义上的模。
L∞范数:就是取向量的最大值。

在机器学习中的应用

正则化在机器学习中经常出现，但是我们常常知其然不知其所以然，今天博主将从正则化对模型的限制、正则化与贝叶斯先验的关系和结构风险最小化三个角度出发，谈谈L1、L2范数被使用作正则化项的原因。博主是初学者，理解有限，若有理解错误的地方还望大家批评指正。

应用一：约束模型的特性:

1.1 L2正则化——让模型变得简单:

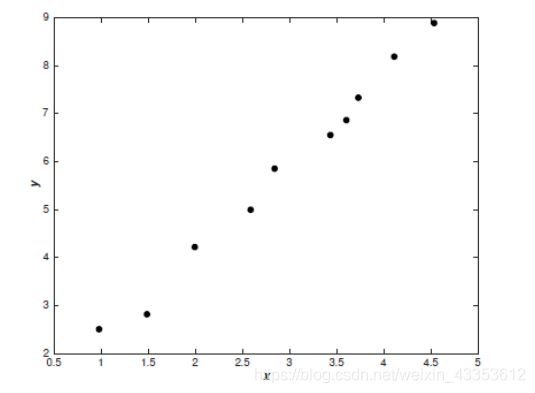
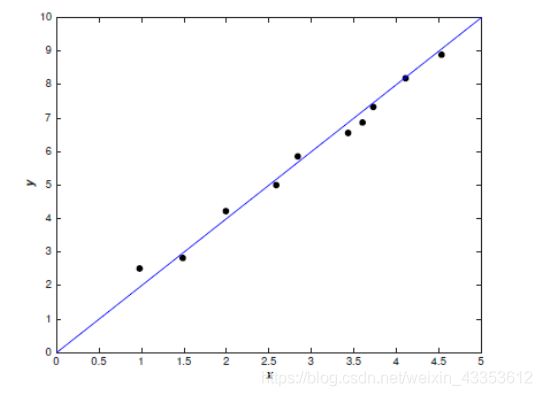
例如我们给下图的点建立一个模型：

我们可以直接建立线性模型：

也可以建立一个多项式模型：

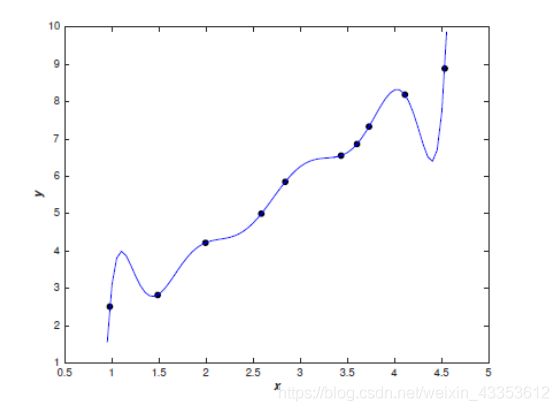
哪种模型更好呢？直观来讲，我们应该会选择线性模型。Occam’s razor定律告诉我们，‘Entities should not be multiplied unnecessarily’。这可以理解为简单的模型肯定比复杂的模型常见，如果一个简单的模型刚好适合拟合这些数据，那么我们会认为这个简单的模型恰好反应出一些潜在的规律。从这个角度来看，尽管多项式模型在已知的数据点上能近似地很好，但这是学习到了数据噪声的结果，在未知的数据的泛化上很有可能存在问题。

奥卡姆剃刀定律（Occam’s Razor, Ockham’s Razor）又称“奥康的剃刀”。
奥卡姆剃刀定律，是由14世纪逻辑学家、圣方济各会修士奥卡姆的威廉（William of Occam，约1285年至1349年）提出。奥卡姆（Ockham）在英格兰的萨里郡，那是他出生的地方。他在《箴言书注》2卷15题说“切勿浪费较多东西去做用较少的东西同样可以做好的事情。”这个原理称为“如无必要，勿增实体”（Entities should not be multiplied unnecessarily）。

这就是我们常说的模型训练中的过拟合现象，即训练集误差在下降，测试集误差在上升。我们认为这是模型学习到了训练集中局部噪声的结果，它虽然在训练集上表现得好，泛化能力却比较差。因此我们需要更简单的模型，这个模型不会受到单个证据的影响，不会因为某个输入的微小变动而产生较大的行为改变。
L2正则化可以解决模型训练中的过拟合现象，它也被称为权重衰减。在回归模型中，这也被称为岭回归。我们先介绍L2正则化的实现方式，然后定性地介绍一下为什么L2正则化可以防止过拟合。
设损失函数为:

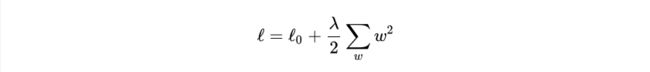
其中 l₀ 表示没有正则化时的损失函数。对它求w的偏导：

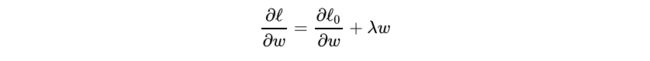
对w进行更新：

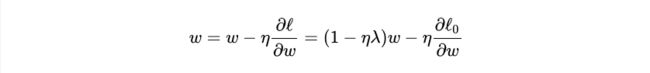
我们知道，没有正则化的参数更新为:

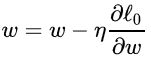
而L2正则化使用了一个乘性因子 (1- ηλ ) 去调整权重，因此权重会不断衰减，并且在权重较大时衰减地快，权重较小时衰减得慢。
下面换一种方式来理解L2正则化对权重的限制。我们的目标是最小化下面的损失函数：

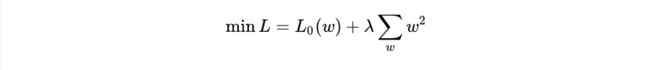
为了 l₀ 最小，需要让 l₀ 和正则化项的和能够最小。若w变大让 l₀ 减小,$$\sum _w(w^2)$$也会变大，后者就会抑制前者，从而让w不会上升地过大。此时 λ 就像是一个调整模型拟合精度与泛化能力的权重因子。

现在我们知道了，L2正则化能够限制参数的大小。那么，为什么参数大小被限制了，这个模型就是一个简单的模型，就能够防止过拟合了呢？回到我们最初开始介绍的多项式回归 y = a₀x⁹ + a₁x⁸ + … + a₉,当参数很小时，高次方项的影响就会变得十分微弱，这使模型不会对某一个输入太过敏感，从而近似学习到一条简单的曲线，类似最开始的线性模型。也就是说，即使你预设的回归模型是一个9次的多项式回归，通过正则化学习，高次项前的系数 会变得很小，最后的曲线类似一条直线，这就是让模型变成了一个简单的模型。

总结一下:

• 正则化让模型根据训练数据中常见的模式来学习相对简单的模型，无正则化的模型用大参数学习大噪声。
• L2正则化通过权重衰减，保证了模型的简单，提高了泛化能力。

1.2 L0、L1正则化——让模型变得稀疏:

我们知道，如果模型中的特征之间有相互关系，会增加模型的复杂程度，并且对整个模型的解释能力并没有提高，这时我们就要进行特征选择。特征选择也会让模型变得容易解释，假设我们要分析究竟是哪些原因触发了事件A，但是现在有1000个可能的影响因子，无从分析。如果通过训练让一部分因子为0，只剩下了几个因子，那么这几个因子就是触发事件A的关键原因。进行特征自动选择，也就是让模型变得稀疏，这可以通过L0和L1范数实现。

L0正则化

L0范数指的是向量中非零元素的个数，L0正则化就是限制非零元素的个数在一定的范围，这很明显会带来稀疏。一般而言，用L0范数实现稀疏是一个NP-hard问题，因此人们一般使用L1正则化来对模型进行稀疏约束。

L1正则化

设损失函数为：

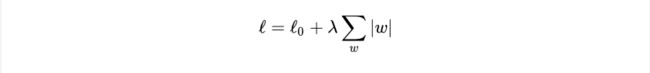
其中 l₀ 表示没有正则化时的损失函数。对它求w的偏导：

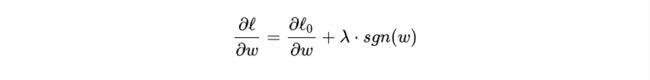
sgn(w)表示w的符号。对w进行更新：

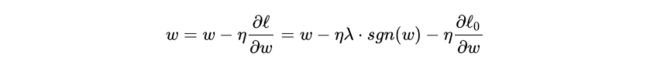
可以看出，L1正则化是通过加上或减去一个常量 ηλ ,让w向0靠近；对比L2正则化，它使用了一个乘性因子 (1 - ηλ )去调整权重，使权重不断衰减。因此可以得出：当 |w| 很大时,L2对权重的衰减速度比L1大得多，当 |w| 很小时，L1对权重的缩小比L2快得多。
这也就解释了为什么L1正则能让模型变得稀疏。L1对于小权重减小地很快，对大权重减小较慢，因此最终模型的权重主要集中在那些高重要度的特征上，对于不重要的特征，权重会很快趋近于0。所以最终权重w会变得稀疏。

1.3 L1、L2正则化的形象理解:

理解一：解的表示

L1、L2正则化还有另一种表示方式：
L1：

L2:

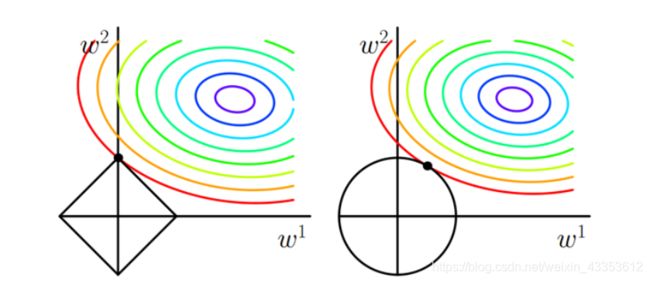
如上图所示，假设w是一个二维的向量，则目标函数可以用一圈圈等值线表示，约束条件用图中黑线表示，而我们要找的最优解，就在等值线和约束线第一次相交的地方。

左图是L1正则化的情况，在特征为二维时，约束线是一个菱形，等值线极有可能最先与顶点相交，在这种情况下有一个维度的特征就会为0，这就带来了稀疏。当特征的维度变高，坐标轴上角与边都会变多，这更会加大等值线与他们先相交的概率，从而导致了稀疏性。

L2正则化不同，如右图所示，它的约束线是一个圆形，等值线可能与它任意一个位置的点首先相切，这个切点在坐标轴上的概率大大 减小，从而不太容易导致稀疏。

理解二：下降速度

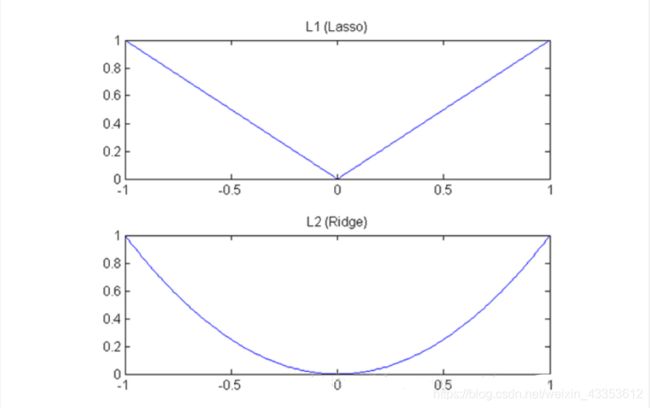
另外从下降速度来看，L1正则化是绝对值函数，L2正则化是二次函数，他们的函数图形如上图所示。可以看出L1正则化的下降速度一直都是一致的，这也符合之间得出的结论：L1正则化通过一个常数:

来让权重减小：

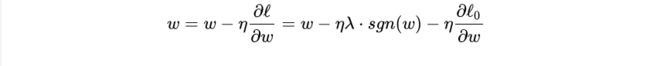
而L2正则化的下降速度不同，当w大的时候，下降较快，当w小的时候，下降较慢，这也符合我们之前推导的，L2正则化通过一个乘性因子

去衰减权重：

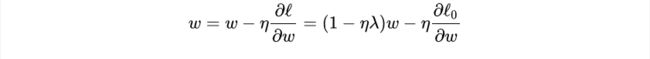
这种差异就导致当w较大时，L2的斜率大于L1，L2正则化权重衰减地比L1正则化快；w小时，L2斜率小于L1，L1正则化权重衰减地比L2正则化快。因此L1正则化最终会导致模型保留了重要的大权重连接，不重要的小权重都被衰减为0，产生了稀疏。而L2正则化可以通过限制权重大小让模型变得简单，但却不会导致稀疏。

应用二：贝叶斯学派中，对应于模型的先验概率

频率学派和贝叶斯学派

频率学派往往通过证据推导一件事情发生的概率，而贝叶斯学派还会同时考虑这个证据的可信度。从参数估计的角度来讲，频率学派认为参数 θ 是固定不变的，虽然我们不知道它，但是我们可以根据一组抽样值去预测它的结果，这就有了极大似然估计（Maximum Likelihood Estimation, MLE）。极大似然估计的思想就是，我已经抽样产生了一组值（例如抛硬币5次，得出结果:正正反正反），那么到底是什么参数（抛一次硬币，正面朝上的概率）才让我最有可能抽样出这一组结果呢。即我的目标是求出让似然函数最大的参数 θ ：

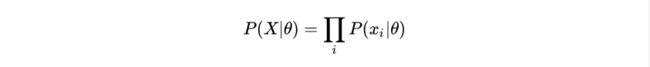
而贝叶斯学派则认为参数 θ 本身就是一个随机变量，它也有自己的分布。如果我们现在已经有一组结果（正正反正反），我们可以根据这个结果求出随机变量 θ 最有可能的值，这其实就是最大后验概率估计(MAP)。最大后验概率估计是要求出 P( θ | X ) 最大的 θ ,我们知道：

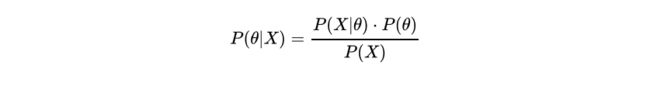
P(X)作为确定值，我们不考虑它，最大后验概率估计变成了：

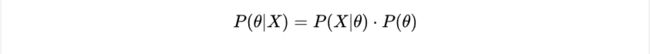
可以看出它只是在极大似然估计的基础上乘上了参数的先验概率，也就是说我求出的参数不仅仅有最大的概率产生这组值（正正反正反），它本身出现的概率也必须大。

举个通俗易懂的例子，如果你出门遇到一位算命师傅，他说你最近有桃花运，果然你不久之后就被心仪的人表白，这说明这个师傅算命很准（记作事件A），现在我们来讨论下这个师傅究竟会不会算命（将师傅会算命记作证据B）。从频率学派的角度来看，如果师傅会算命（证据B发生），那么他算对了我的桃花运是一件概率很大的事情。也就是说P(A|B)很大，从极大似然的角度讲，我们应该相信师傅会算命。可事实上我们根本不会相信师傅会算命，因为我们本身对会算命这件事有着先验的不相信，也就是说在我们眼中，P(B)是很小的。这说明我们已经潜移默化地用了贝叶斯思想，在最大后验概率估计中，P(B|A) ~ P(A|B)P(B)，即使P(A|B)很大，如果P(B)很小，那么P(B|A)还是会小。

先验概率与L1、L2范数

当模型的目标函数是最大化后验概率 P( w| X) ,即最大化：

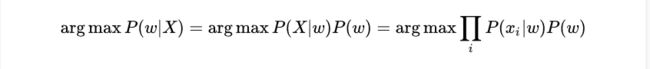
连乘导致下溢，我们取负对数将其转化为最小化损失函数：

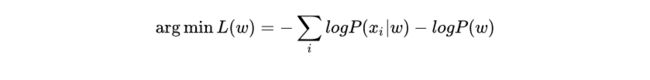
下面我们将证明参数的先验概率如何变成了损失函数的正则化项。

• （1）假设 w 的先验分布是高斯分布 w ~ N( 0, σ² ),则：
  
  其中m表示w的向量维度。最终目标函数为最小化：
  其中：

最终先验概率转变成了L2正则化项。

• (2) 假设w的先验分布时拉普拉斯分布，则：
  
  其中m表示w的向量维度。最终目标函数为最小化：
  
  其中 λ = 1/b，最终先验概率转变成了L1正则化项。
  

总结一下:

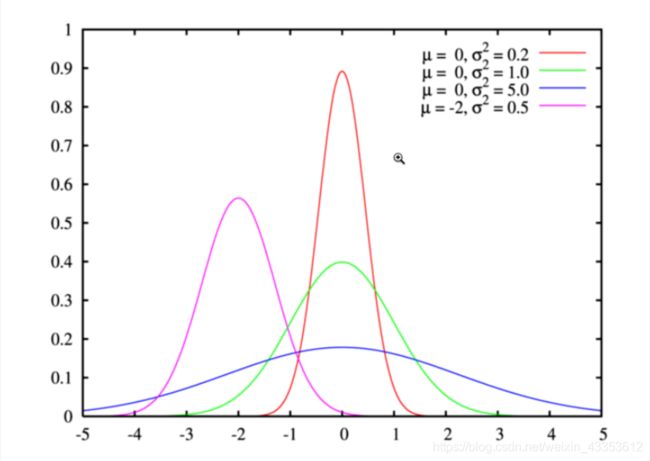
• 概率目标函数通过负对数转化，将正态分布和拉普拉斯分布的指数项转变成了普通的一次、二次项；
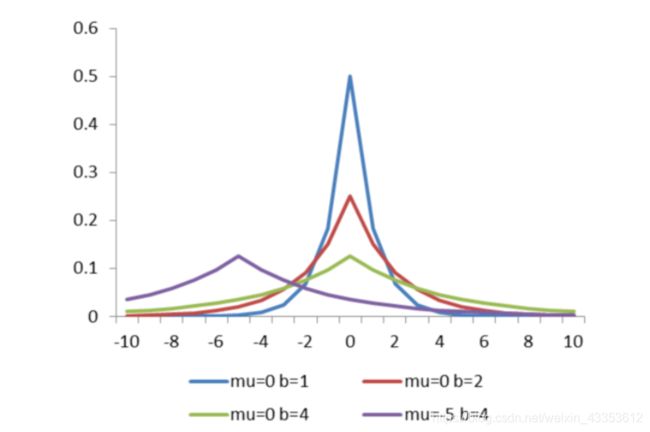
• 先验分布为高斯分布，对于损失函数的L2正则化项，先验分布为拉普拉斯分布，对应损失函数的L1正则化项。

应用三：结构风险最小化

首先介绍一下什么是期望风险、经验风险和结构风险。在机器学习的目标中，理论上我们应该尽力让期望风险（期望损失,expected loss）最小化：

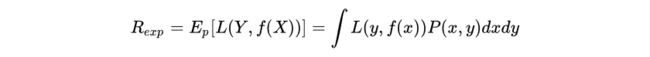
但实际上，联合分布P(X,Y)我们是不可能知道的，因此在实际训练中，我们常常最小化经验风险（经验损失, empirical loss）：

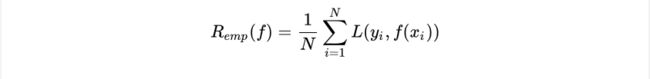
期望风险是模型关于联合分布的期望损失，经验风险是模型关于训练样本集的平均损失，当N趋近于无穷时，经验风险趋近于期望风险，因此我们可以用经验风险最小化去近似期望风险最小化。
然而，我们的训练集样本数量N很有限，用经验风险估计近似期望风险往往不理想，容易产生“过拟合”的现象，因此需要使用结构风险来矫正经验风险。
结构风险(structural risk)最小化的目的是防止过拟合，它是在经验风险上加上表示模型复杂度的正则化项：

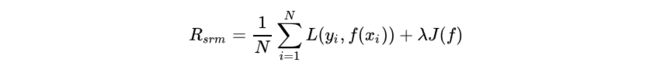
其中J(f)为模型的复杂度。结构风险最小化的目标就是让经验风险与模型复杂度同时小。监督学习的问题实际上也就是经验风险或结构风险最小化问题，对于样本容量大的情况，经验风险最小化可以达到很好的效果，例如极大似然估计；当样本容量不够时，需要使用结构风险最小化来避免过拟合，例如最大后验概率估计，其模型的复杂度由模型的先验概率表示。

以上三种应用的统一

• 结构风险其实是让经验风险与模型复杂度同时小，实际上也是在约束模型的特性。
• 正则化可以约束模型的特性。简单的模型还是稀疏的模型，实际上都来自与我们对这个模型的事先感知，从贝叶斯的角度来理解，也可以认为这是模型的先验。
• 而结构风险是在经验风险后面加上表示模型复杂度的正则化项，最大后验概率估计就是最小化的结构风险，它的模型复杂度由模型的先验概率表示。当模型的先验分布为高斯分布时，认为模型复杂度是平方复杂度；当模型的先验分布为拉普拉斯分布时，认为模型的复杂度是绝对值复杂度。
• 总的来说可以理解为：结构风险考虑了约束模型的特性，模型的特性是由模型的先验知识确定的，先验的不同导致了L1、L2正则化项的不同使用。

二.矩阵范数：

引入

共轭转置矩阵

A^*指的是A的共轭转置矩阵，也有A^H这个写法。如果A里面全是实数，那效果就与A^T无二；如果A里面也有复数，则是先对A取共轭（各项实部不变，虚部取相反数），然后再转置，比如：

A =
       1.0000 + 0.0000i   0.0000 - 2.0000i
       3.0000 + 0.0000i   0.0000 - 4.0000i
>> A'
ans =
       1.0000 + 0.0000i   3.0000 + 0.0000i
       0.0000 + 2.0000i   0.0000 + 4.0000i

在matlab中A’的意思就是求共轭转置矩阵。

特征值

矩阵A的特征值被定义为：A$v$=λ$v$
其中 $v$ 被称为“矩阵A的特征向量”，λ被称为“矩阵A的特征值”。
在matlab中求解矩阵A的特征值方法如下：

A =
       1     2     3
       4     5     6
       7     8     9
>> [V,D] = eig(A)
V =
       -0.2320   -0.7858    0.4082
       -0.5253   -0.0868   -0.8165
       -0.8187    0.6123    0.4082
D =    
       16.1168         0         0
             0   -1.1168         0
             0         0   -0.0000

矩阵V的每一列都是一个特征向量，D中对应列中的值即与该特征向量相匹配的特征值。以上例V、D第一列为例，此时特征值λ=16.1168，特征向量 $v$ =[−0.2320,−0.5253,−0.8187]^T，用matlab作验证如下：

>> A = [1,2,3;4,5,6;7,8,9]
A =
       1     2     3
       4     5     6
       7     8     9
>> v = [-0.2320,-0.5253,-0.8187]'
v =
       -0.2320
       -0.5253
       -0.8187   
>> lambda = 16.1168
lambda =
       16.1168
>> A * v
ans =
       -3.7387
       -8.4667
      -13.1947
>> lambda * v  
ans =
       -3.7391
       -8.4662
      -13.1948 

可知满足 A$v$=λ$v$。

1、矩阵的1-范数（列模） ：

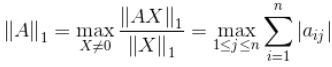
矩阵的每一列上的元素绝对值先求和，再从中取个最大的，（列和最大）。

A =
     1     2     3
     4     5     6
     7     8     9
>> norm_1 = norm(A,1)
norm_1 =
    18

第一列求和结果为：|1|+|4|+|7|=12
第二列求和结果为：|2|+|5|+|8|=15
第三列求和结果为：|3|+|6|+|9|=18
里面最大的就是18，因此矩阵A的列和范数为18。
Matlab代码: norm(A,1);

2、矩阵的2-范数（谱模）：

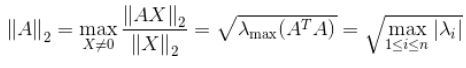
其中, λ 为 AA^* 的特征值,矩阵的2-范数即对矩阵 AA^T 的最大特征值开平方根。

>> [V,D] = eig(A'*A)
V = 
   -0.4082   -0.7767    0.4797
    0.8165   -0.0757    0.5724
   -0.4082    0.6253    0.6651

D =
    0.0000         0         0
         0    1.1414         0
         0         0  283.8586
>> sqrt(283.8586)
ans =
   16.8481

（这里最大特征值为283.8586）
当然，matlab中也有更直接的计算矩阵2-范数的方法，如下：

>> norm_2 = norm(A,2)
norm_2 = 
      16.8481

两种方法计算出的结果是一样的。
Matlab代码：norm(A,2);

3、矩阵的无穷范数（行模）：

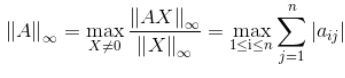
和1-范数（列和范数）类似，这里是沿行方向取绝对值求和，将最大的那个值作为矩阵的∞-范数。matlab代码如下：

>> A
A =
     1     2     3
     4     5     6
     7     8     9
>> norm(A,inf)
ans =
    24
第一行求和结果为：|1|+|2|+|3|=6 
第二行求和结果为：|4|+|5|+|6|=15 
第三行求和结果为：|7|+|8|+|9|=24 
里面最大的就是24，因此矩阵A的行和范数为24。

4、矩阵的核范数：

矩阵的核范数即：矩阵的奇异值（将矩阵svd分解）之和，这个范数可以用来低秩表示（因为最小化核范数，相当于最小化矩阵的秩——低秩）。

矩阵奇异值:

设A是一个mXn矩阵，称正半定矩阵A‘A的特征值的非负平方根为矩阵A的奇异值，其中A‘表示矩阵A的共扼转置矩阵.

奇异矩阵：

奇异矩阵是线性代数的概念，就是该矩阵的秩不是满秩。首先，看这个矩阵是不是方阵（即行数和列数相等的矩阵。若行数和列数不相等，那就谈不上奇异矩阵和非奇异矩阵）。然后，再看此矩阵的行列式|A|是否等于0，若等于0，称矩阵A为奇异矩阵；若不等于0，称矩阵A为非奇异矩阵。同时，由|A|≠0可知矩阵A可逆，这样可以得出另外一个重要结论：可逆矩阵就是非奇异矩阵，非奇异矩阵也是可逆矩阵。 如果A为奇异矩阵，则AX=0有无穷解，AX=b有无穷解或者无解。如果A为非奇异矩阵，则AX=0有且只有唯一零解，AX=b有唯一解。
SVD奇异值分解！！！详细见此！

例如矩阵A = [ -1 2 -3；
4 -6 6]
上述矩阵A最终结果就是：10.9287， MATLAB代码实现为：sum(svd(A)).

5、矩阵的F范数：

矩阵的F范数即：矩阵的各个元素平方之和再开平方根，它通常也叫做矩阵的L2范数，它的有点在它是一个凸函数，可以求导求解，易于计算。
例如矩阵A = [ -1 2 -3；
4 -6 6]
上述矩阵A最终结果就是：10.0995，MATLAB代码实现为：norm（A，‘fro’）.

5、矩阵的L21范数：

矩阵的L21范数即：矩阵先以每一列为单位，求每一列的F范数（也可认为是向量的2范数），然后再将得到的结果求L1范数（也可认为是向量的1范数），很容易看出它是介于L1和L2之间的一种范数。
例如矩阵A = [ -1 2 -3；
4 -6 6]
上述矩阵A最终结果就是：17.1559，MATLAB代码实现为： norm(A(:,1),2) + norm(A(:,2),2) + norm(A(:,3),2).

矩阵范数的实际应用： 机器学习应用

谈了那么多的范数，那么 L0, L1, L2 中的 L 到底代表什么呢？其实 L 代表了法国数学家 Henri Léon Lebesgue (昂利・莱昂・勒貝格)，另一个著名的勒贝格积分也是以他命名的。