支持向量机SVM(一)原始函数与对偶函数
此篇文章对支持向量机推导过程进行详解,仅作为本人纪录一遍对SVM的复习过程。
所有公式已做手动推导,为了美观(字丑),将选择贴出周老先生西瓜书的一些结论和李航统计机器学习和南瓜书推导过程。
该系列其他文章
SVM系列二:支持向量机SVM(二)Kernel核函数
SVM系列三:支持向量机SVM(三)软间隔与松弛变量的替代损失函数
间隔与支持向量
先贴一副情况图作为开头。

如上图,SVM 的主要思想是找到几何间隔最大的超平面对数据进行正确划分,中间那条黑线将会是我们的超平面。
主观上来看,它具有更强的鲁棒性,因为他距离样本两边都有合适的距离,泛化能力会更强。
将超平面以线性方程描述
ω T x + b = 0 (公式1) \omega ^T x + b = 0\tag{公式1} ωTx+b=0(公式1)
而样本空间内任一点x到达超平面(w,b)的距离可写为
r = ∣ ω T x + b ∣ ∥ ω ∥ (公式2) r = \frac{|\omega ^T x + b|}{\left \| \omega \right \|} \tag{公式2} r=∥ω∥∣ωTx+b∣(公式2)
倘若超平面能正确分类,则如下图所示。
距离超平面最近的训练样本被称为“支持向量”。
两边的支持向量满足 ω x + b = y , ( y = 1 或 − 1 ) \omega x+b=y,(y=1或-1) ωx+b=y,(y=1或−1),其身后的所有样本都有 ω x + b > y , ( y = 1 或 − 1 ) \omega x+b >y,(y=1或-1) ωx+b>y,(y=1或−1)。
当然,假如最优的超平面确认下来,后方所有点都将会弃之不用,这也是SVM的重要性质,将大大节省计算和存储。

两个异类支持向量之间的距离之和为间隔(公式3),该式的函数间隔值2是根据公式2和上图计算得出。但事实上,函数间隔并不影响最优化问题的解,所以可以等价替换。
γ = 2 ∥ ω ∥ (公式3) \gamma = \frac{2}{\left \| \omega \right \|} \tag{公式3} γ=∥ω∥2(公式3)
要找到最优的超平面,我们需要找到支持向量之间的最大间隔,间隔函数将作为我们的目标函数。由于支持向量位于 ω x + b = 1 \omega x + b = 1 ωx+b=1与 ω x + b = − 1 \omega x + b = -1 ωx+b=−1的直线上,我们在前面乘上一个该点所属的类别y,就可以得到支持向量的表达式为: y ( ω x + b ) = 1 y(\omega x + b) = 1 y(ωx+b)=1,这将作为我们约束的条件。
目标函数及其约束条件如下
m a x ω , b = 2 ∥ ω ∥ s . t . y i ( ω T x + b ) ⩾ 1 , i = 1 , 2 , . . . , m . (公式4) \begin{aligned} & \underset{\omega , b}{max} = \frac{2}{\left \| \omega \right \|} \\ & s.t. \ yi(\omega ^T x + b )\geqslant 1 , \quad i=1,2,...,m. \end{aligned}\tag{公式4} ω,bmax=∥ω∥2s.t. yi(ωTx+b)⩾1,i=1,2,...,m.(公式4)
得到最大间隔,也就相当于得到了最优超平面,而且超平面的存在是唯一的。
为了最大化间隔γ,我们一般会选择固定函数间隔为2,这时只需要最大化 1 ∥ ω ∥ \frac{1}{\left \| \omega \right \|} ∥ω∥1,也就是最小化 ∥ ω ∥ \left \| \omega \right \| ∥ω∥,因为分子越小值越大。为了方便求导,我们对 ∥ ω ∥ \left \| \omega \right \| ∥ω∥二范式进行平方,这等价于最小化 ∥ ω ∥ \left \| \omega \right \| ∥ω∥,系数更为1/2。
为什么能这么做? 1 ∥ ω ∥ \frac{1}{\left \| \omega \right \|} ∥ω∥1的导数是 − 1 ∥ ω ∥ 2 < 0 \frac{-1}{\left \| \omega \right \|^2}<0 ∥ω∥2−1<0,单调递减,而 1 2 ∥ ω ∥ 2 \frac{1}{2} \left \| \omega \right \|^2 21∥ω∥2 的导数为 ∥ ω ∥ > 0 \left \| \omega \right \|>0 ∥ω∥>0,单调递增,所以当 1 ∥ ω ∥ \frac{1}{\left \| \omega \right \|} ∥ω∥1不断减小的时候, 1 2 ∥ ω ∥ 2 \frac{1}{2} \left \| \omega \right \|^2 21∥ω∥2是在不断增加的,因此当 1 ∥ ω ∥ \frac{1}{\left \| \omega \right \|} ∥ω∥1取得最小值的时候, 1 2 ∥ ω ∥ 2 \frac{1}{2} \left \| \omega \right \|^2 21∥ω∥2自然取得最大值。 1 2 ∥ ω ∥ 2 \frac{1}{2} \left \| \omega \right \|^2 21∥ω∥2取任意大于等于2的正整数次方均可,前面乘上正常数都可以,之所以取2,是使得问题相对简化的同时,又比 ∥ ω ∥ \left \| \omega \right \| ∥ω∥增长速度更快,收敛的速度也相对较快,因此取2次方。(此段话转自知乎)
最终得到以下目标函数
m i n ω , b = 1 2 ∥ ω ∥ 2 s . t . y i ( ω T x + b ) ⩾ 1 , i = 1 , 2 , . . . , m . (公式5) \begin{aligned} & \underset{\omega , b}{min} = \frac{1}{2}\left \| \omega \right \|^2 \\ & s.t. \ yi(\omega ^T x + b )\geqslant 1 , \quad i=1,2,...,m.\\ \end{aligned}\tag{公式5} ω,bmin=21∥ω∥2s.t. yi(ωTx+b)⩾1,i=1,2,...,m.(公式5)
拉格朗日对偶问题(dual)
对于目标函数(公式5),这是一个凸二次优化问题,但是可以通过拉格朗日对偶性将原始问题转化为对偶问题,通过对偶问题来求原始问题的解。因为对偶问题更容易求解,二是自然引进核函数,进而推广到非线性分类问题。
首先构造拉格朗日函数(公式6),对每一个不等式约束添加拉格朗日乘子 α ≥ 0 , i = 1 , 2 , 3 , . . . N \alpha \geq 0 \ ,i=1,2,3,...N α≥0 ,i=1,2,3,...N。
L ( ω , b , α ) = 1 2 ∥ ω ∥ 2 + ∑ i = 1 n α i ( 1 − y i ( ω T x i + b ) ) (公式6) L(\omega ,b,\alpha ) = \frac{1}{2}\left \| \omega \right \|^2 + \sum_{i = 1}^{n}\alpha _{i}(1-y_{i}(\omega ^{T}x_{i}+b)) \tag{公式6} L(ω,b,α)=21∥ω∥2+i=1∑nαi(1−yi(ωTxi+b))(公式6)
在满足KKT条件下,原始问题的求解可以转换成对偶问题来求解,强对偶成立,而强对偶成立,又一定满足KKT条件。(原始问题可以证明等价为极小极大问题,符合KKT条件的话可以证明等价为极大极小问题,这里不证明了,可以看这篇博客:机器学习数学:拉格朗日对偶问题)
{ α i ⩾ 0 ; y i f ( x i − 1 ) ⩾ 0 ; α i ( y i f ( x i ) − 1 ) = 0. \left\{\begin{matrix} \alpha_{i}\geqslant 0; \\ y_{i}f(x_{i}-1)\geqslant 0; \\ \alpha _{i}(y_{i}f(x_{i})-1)=0. \end{matrix}\right. ⎩⎨⎧αi⩾0;yif(xi−1)⩾0;αi(yif(xi)−1)=0.
于是根据拉格朗日对偶性,原始问题(等价于极小极大问题)可以转化成一个最优解等价的对偶极大极小问题。
m a x α i ≥ 0 m i n ω , b L ( ω , b , α ) {\underset{\alpha _{i}\geq 0}{max}}\ \underset{\omega ,b}{min}\ L(\omega ,b,\alpha ) αi≥0max ω,bmin L(ω,b,α)
为了得到对偶问题的解,需要先对 L ( ω , b , α ) L(\omega,b,α) L(ω,b,α)对w,b求极小,再求对α的极大,也就是先后求偏导
先展开,如下式
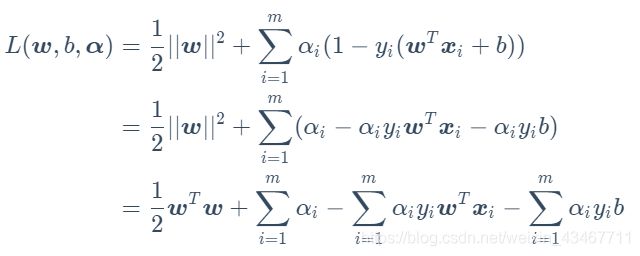
对 ω , b \omega,b ω,b求偏导
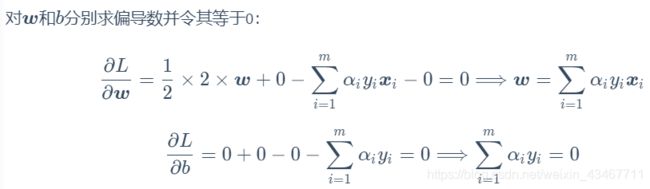
最后得到
ω = ∑ i = 1 m α i y i x i , 0 = ∑ i = 1 m α i y i \begin{aligned} \omega =& \sum_{i=1}^{m}\alpha _{i}y_{i}x_{i},\\ 0 = & \sum_{i=1}^{m} \alpha _{i}y_{i} \end{aligned} ω=0=i=1∑mαiyixi,i=1∑mαiyi
将上式代入拉格朗日函数

然后再求 m i n ( L ( ω , b , α ) ) min(L(\omega,b,α)) min(L(ω,b,α))对α的极大,就得到对偶变量α的优化问题了。
m a x α m i n ω , b L ( ω , b , α ) = m a x α ∑ i = 1 m α i − 1 2 ∑ i = 1 m ∑ j = 1 m α i α j y i y j x i T x j s . t . ∑ i = 1 m α i y i = 0 , α i ⩾ 0 , i = 1 , 2 , . . . , m . \begin{aligned} & \underset{\alpha}{max}\ \underset{\omega,b}{min}\ L(\omega ,b,\alpha ) =\underset{\alpha}{max}\sum_{i=1}^{m} \alpha _{i} -\frac{1}{2}\sum_{i=1}^{m} \sum_{j=1}^{m} \alpha _{i}\alpha _{j}y_{i}y_{j}x_{i}^Tx_{j} \\ & s.t. \ \sum_{i=1}^{m}\alpha _{i}y_{i} = 0,\\ & \qquad\alpha _{i}\geqslant 0,\quad i=1,2,...,m. \end{aligned} αmax ω,bmin L(ω,b,α)=αmaxi=1∑mαi−21i=1∑mj=1∑mαiαjyiyjxiTxjs.t. i=1∑mαiyi=0,αi⩾0,i=1,2,...,m.
以上就是原始函数的对偶问题,对偶函数求α虽然是一个二次规划问题,但一般我们用更高效的SMO算法求解,这里就不多赘述。
对于一个数据点 x 进行分类,实际上是通过把 x 带入到 f ( x ) = ω x + b f(x)= \omega x+b f(x)=ωx+b算出结果然后根据其正负号来进行类别划分的。而前面的推导中我们以及得到 w的值 ,因此可得模型。
f ( x ) = ω T x + b = ∑ i = 1 m α i y i x i T x + b . f(x) = \omega^Tx +b = \sum_{i=1}^{m} \alpha_{i}y_{i}x_{i}^Tx + b \ . f(x)=ωTx+b=i=1∑mαiyixiTx+b .
这里补充一下SVM只保留支持向量机的情况,参考的该大佬的博客。
pluskid大佬
对于新点 x 的预测,也只需要计算它与训练数据点xi的内积即可,这一点至关重要,是之后使用 Kernel 进行非线性推广的基本前提。此外,所谓支持向量也在这里显示出来——事实上,所有非支持向量所对应的系数 α 都是等于零的,因此对于新点的内积计算实际上只要针对少量的“支持向量”而不是所有的训练数据即可。
回想我们之前的拉格朗日目标函数
m a x α i ≥ 0 L ( ω , b , α ) = m a x α i ≥ 0 1 2 ∥ ω ∥ 2 − ∑ i = 1 n α i ( y i ( ω T x i + b ) − 1 ) \underset{\alpha _{i}\geq 0}{max} L(\omega ,b,\alpha ) =\underset{\alpha _{i}\geq 0}{max} \ \frac{1}{2}\left \| \omega \right \|^2 - \sum_{i=1}^{n} \alpha _{i} {\color{Red} (y_{i}(\omega ^T x_{i}+b)-1)} αi≥0maxL(ω,b,α)=αi≥0max 21∥ω∥2−i=1∑nαi(yi(ωTxi+b)−1)
如果 x i x_{i} xi 是支持向量的话,上式中红颜色的部分是等于 0 的,因为 y ( ω x + b ) = 1 y(\omega x + b) = 1 y(ωx+b)=1,而对于不是支持向量的来说, y ( ω x + b ) y(\omega x + b) y(ωx+b)结果会>1,而红色部分的约束式就会>0, α α α又只能>=0,为了避免最大间隔缩水, α α α只能等于0了,所以非支持向量对支持向量机一点影响都没有。
下一篇博客将推导介绍SVM最重要的核功能,那是灵魂所在。
支持向量机SVM(二)Kernel核函数