【二叉搜索树】1305. 两棵二叉搜索树中的所有元素（非递归中序遍历）

题目

给你 root1 和 root2 这两棵二叉搜索树。

请你返回一个列表，其中包含 两棵树 中的所有整数并按 升序 排序。.

示例 1：

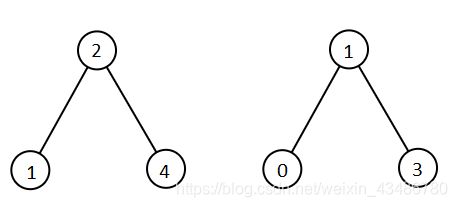
输入：root1 = [2,1,4], root2 = [1,0,3]
输出：[0,1,1,2,3,4]

示例 2：

输入：root1 = [0,-10,10], root2 = [5,1,7,0,2]
输出：[-10,0,0,1,2,5,7,10]

示例 3：

输入：root1 = [], root2 = [5,1,7,0,2]
输出：[0,1,2,5,7]

示例 4：

输入：root1 = [0,-10,10], root2 = []
输出：[-10,0,10]

示例 5：

输入：root1 = [1,null,8], root2 = [8,1]
输出：[1,1,8,8]

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/all-elements-in-two-binary-search-trees
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

---

最简单的思路是遍历两棵树，将所有元素放到一个数组里，然后对数组排序。

由于二叉搜索树本来就是有序的，因此本文采用的是同时中序遍历两颗二叉搜索树，这里需要采用非递归的方式中序遍历二叉树，代码如下

public void InOrder(TreeNode root) {
	Stack<TreeNode> stack = new Stack<>();
	TreeNode curNode = root;
	while (curNode != null || !stack.isEmpty()) {
		while (curNode != null) {
			// 将所有左孩子入队
			stack.push(curNode);
			curNode = curNode.left;
		}
		if (!stack.isEmpty()) {
			TreeNode tmpNode = stack.pop();
			System.out.print(tmpNode.val + " ");
			curNode = tmpNode.right; // 移动到右孩子处（可能为null）
		}
	}
}

基于上述代码，同时中序遍历两颗二叉树，在遍历时，分别比较栈顶元素的大小，把小的元素添加到结果列表中，然后移动小元素所在的二叉树（即访问下一个节点），而另一颗二叉树不动，直到他的栈顶元素比另一颗树的小时才访问其它节点。

需要注意当有一个栈为空时，则表明其中一颗二叉树已经访问完了，此时只需中序遍历另一颗树即可。

class Solution {
	public List<Integer> getAllElements(TreeNode root1, TreeNode root2) {
		Stack<TreeNode> stack1 = new Stack<>(), stack2 = new Stack<>();
		TreeNode curNode1 = root1, curNode2 = root2;
		List<Integer> res = new LinkedList<>();
		while (curNode1 != null || !stack1.isEmpty() || curNode2 != null || !stack2.isEmpty()) {
			while (curNode1 != null) {
				stack1.push(curNode1);
				curNode1 = curNode1.left;
			}
			while (curNode2 != null) {
				stack2.push(curNode2);
				curNode2 = curNode2.left;
			}
			if (stack1.isEmpty()) {
				// 中序遍历stack2
				TreeNode topNode2 = stack2.pop();
				res.add(topNode2.val);
				curNode2 = topNode2.right;
			} else if (stack2.isEmpty()) {
				// 中序遍历stack1
				TreeNode topNode1 = stack1.pop();
				res.add(topNode1.val);
				curNode1 = topNode1.right;
			} else {
				TreeNode topNode1 = stack1.peek();
				TreeNode topNode2 = stack2.peek();
				if (topNode1.val <= topNode2.val) {
					stack1.pop();
					res.add(topNode1.val);
					curNode1 = topNode1.right;
				} else {
					stack2.pop();
					res.add(topNode2.val);
					curNode2 = topNode2.right;
				}
			}
		}
		return res;
	}
}