第12章 计算学习理论
第12章 计算学习理论
12.1 基础知识
计算机学习理论(computational learning theory)研究通过计算来进行学习的理论,即关于机器学习的理论基础,其目的是分析学习任务的困难本质。
给定样例集 D = { ( x 1 , y 1 ) , ( x 2 , y 2 ) , … , ( x m , y m ) } , x i ∈ X , y i ∈ Y = { − 1 , + 1 } D = \left\{ \left( x_{1},y_{1} \right),\left( x_{2},y_{2} \right),\ldots,\left( x_{m},y_{m} \right) \right\},x_{i}\mathcal{\in X,}y_{i}\mathcal{\in Y =}\left\{ - 1, + 1 \right\} D={(x1,y1),(x2,y2),…,(xm,ym)},xi∈X,yi∈Y={−1,+1},假设 X \mathcal{X} X中的所有样本服从一个隐含未知的分布 D \mathcal{D} D,D中所有样本都是独立地从这个分布上采样而得。
令h为从 X \mathcal{X} X到 Y \mathcal{Y} Y的一个映射,其泛化误差为
E ( h , D ) = P x ∼ D ( h ( x ) ≠ y ) E\left( h,\mathcal{D} \right) = P_{x\sim\mathcal{D}}\left( h\left( x \right) \neq y \right) E(h,D)=Px∼D(h(x)̸=y)
H在D上的经验误差为
E ^ ( h ; D ) = 1 m ∑ i = 1 m I ( h ( x i ) ≠ y i ) \hat{E}\left( h;D \right) = \frac{1}{m}\sum_{i = 1}^{m}{\mathbb{I}\left( h\left( x_{i} \right) \neq y_{i} \right)} E^(h;D)=m1i=1∑mI(h(xi)̸=yi)
误差参数:用 ϵ \epsilon ϵ表示预先设定的学得模型所应满足的误差要求。
常用不等式
Jensen不等式:对任意凸函数 f ( x ) f\left( x \right) f(x),有
f ( E ( x ) ) ≤ E ( f ( x ) ) f\left( \mathbb{E}\left( x \right) \right)\mathbb{\leq E}\left( f\left( x \right) \right) f(E(x))≤E(f(x))
Hoeffding不等式:若 x 1 , x 2 , … , x m x_{1},x_{2},\ldots,x_{m} x1,x2,…,xm为m个独立随机变量,且满足 0 ≤ x i ≤ 1 0 \leq x_{i} \leq 1 0≤xi≤1,则对任意 ϵ > 0 \epsilon > 0 ϵ>0,有
P ( 1 m ∑ i = 1 m x i − 1 m ∑ i = 1 m E ( x i ) ≥ ϵ ) ≤ e x p ( − 2 m ϵ 2 ) P\left( \frac{1}{m}\sum_{i = 1}^{m}{x_{i} - \frac{1}{m}}\sum_{i = 1}^{m}{\mathbb{E}\left( x_{i} \right)} \geq \epsilon \right) \leq exp\left( - 2m\epsilon^{2} \right) P(m1i=1∑mxi−m1i=1∑mE(xi)≥ϵ)≤exp(−2mϵ2)
P ( ∣ 1 m ∑ i = 1 m x i − 1 m ∑ i = 1 m E ( x i ) ∣ ≥ ϵ ) ≤ 2 e x p ( − 2 m ϵ 2 ) P\left( \left| \frac{1}{m}\sum_{i = 1}^{m}{x_{i} - \frac{1}{m}}\sum_{i = 1}^{m}{\mathbb{E}\left( x_{i} \right)} \right| \geq \epsilon \right) \leq 2exp\left( - 2m\epsilon^{2} \right) P(∣∣∣∣∣m1i=1∑mxi−m1i=1∑mE(xi)∣∣∣∣∣≥ϵ)≤2exp(−2mϵ2)
MeDiarmid不等式:若 x 1 , x 2 , … , x m x_{1},x_{2},\ldots,x_{m} x1,x2,…,xm为m个独立随机变量,且对任意 1 ≤ i ≤ m 1 \leq i \leq m 1≤i≤m,函数f满足
sup ∣ f ( x 1 , x 2 , … , x m ) − f ( x 1 , … , x i − 1 , x i ′ , x i + 1 … , x m ) ∣ ≤ c i x 1 , x 2 , … , x m , x i , \frac{\sup\left| f\left( x_{1},x_{2},\ldots,x_{m} \right) - f\left( x_{1},\ldots,x_{i - 1},x_{i}^{'},x_{i + 1}\ldots,x_{m} \right) \right| \leq c_{i}}{x_{1},x_{2},\ldots,x_{m},x_{i}^{,}} x1,x2,…,xm,xi,sup∣∣∣f(x1,x2,…,xm)−f(x1,…,xi−1,xi′,xi+1…,xm)∣∣∣≤ci
则对任意 ϵ > 0 \epsilon > 0 ϵ>0,有
P ( f ( x 1 , x 2 , … , x m ) − E ( f ( x 1 , x 2 , … , x m ) ) ≥ ϵ ) ≤ e x p ( − 2 ϵ 2 ∑ i c i 2 ) P\left( f\left( x_{1},x_{2},\ldots,x_{m} \right)\mathbb{- E}\left( f\left( x_{1},x_{2},\ldots,x_{m} \right) \right) \geq \epsilon \right) \leq exp\left( \frac{- 2\epsilon^{2}}{\sum_{i}^{}c_{i}^{2}} \right) P(f(x1,x2,…,xm)−E(f(x1,x2,…,xm))≥ϵ)≤exp(∑ici2−2ϵ2)
P ( ∣ f ( x 1 , x 2 , … , x m ) − E ( f ( x 1 , x 2 , … , x m ) ) ∣ ≥ ϵ ) ≤ 2 e x p ( − 2 ϵ 2 ∑ i c i 2 ) P\left( \left| f\left( x_{1},x_{2},\ldots,x_{m} \right)\mathbb{- E}\left( f\left( x_{1},x_{2},\ldots,x_{m} \right) \right) \right| \geq \epsilon \right) \leq 2exp\left( \frac{- 2\epsilon^{2}}{\sum_{i}^{}c_{i}^{2}} \right) P(∣f(x1,x2,…,xm)−E(f(x1,x2,…,xm))∣≥ϵ)≤2exp(∑ici2−2ϵ2)
12.2 PAC学习
PAC辨识(PAC Identify):对 ϵ < 0 , δ < 1 \epsilon < 0,\delta < 1 ϵ<0,δ<1,所有 c ∈ C c\mathcal{\in C} c∈C和分布 D \mathcal{D} D,若存在学习算法 L \mathcal{L} L,其输出假设 h ∈ H h\mathcal{\in H} h∈H满足
P ( E ( h ) ≤ ϵ ) ≥ 1 − δ P\left( E\left( h \right) \leq \epsilon \right) \geq 1 - \delta P(E(h)≤ϵ)≥1−δ
则称学习算法 L \mathcal{L} L能从假设空间 H \mathcal{H} H中的PAC辨识概念类 C \mathcal{C} C
PAC可学习(PAC learnable):令m表示从分布 D \mathcal{D} D中独立同分布采样得到的样例数目, ϵ < 0 , δ < 1 \epsilon< 0,\delta <1 ϵ<0,δ<1,对所有分布 D \mathcal{D} D,若存在学习算法 L \mathcal{L} L和多项式函数 poly ( . , . , . ) \text{poly}\left(.,.,. \right) poly(.,.,.),使得对于任何 m ≥ p l o y ( 1 ϵ , 1 δ , s i z e ( x ) , s i z e ( c ) ) m \geq ploy\left(\frac{1}{\epsilon},\frac{1}{\delta},{size\left( x \right),size\left( c \right)} \right) m≥ploy(ϵ1,δ1,size(x),size(c)), L \mathcal{L} L能从假设空间 H \mathcal{H} H中PAC辨识概念类 C \mathcal{C} C,则称概念类 C \mathcal{C} C对假设空间 H \mathcal{H} H而言是PAC可学习的,有时也称概念类 C \mathcal{C} C是PAC可学习的
PAC学习算法(PAC Learning Algorithm):若学习算法 L \mathcal{L} L使概念类 C \mathcal{C} C为PAC可学习的,且 L \mathcal{L} L的运行时间也是多项式函数 ploy ( 1 ϵ , 1 δ , s i z e ( x ) , s i z e ( c ) ) \text{ploy}\left( \frac{1}{\epsilon},\frac{1}{\delta}{,size\left( x \right),size\left( c \right)} \right) ploy(ϵ1,δ1,size(x),size(c)),则称概念类 C \mathcal{C} C是高效PAC可学习的(efficiently PAC Learnable),称 L \mathcal{L} L为概念类 C \mathcal{C} C的PAC学习算法
样本复杂度(Sample Complexity):满足PAC学习算法 L \mathcal{L} L所需的 m ≥ p l o y ( 1 ϵ , 1 δ , s i z e ( x ) , s i z e ( c ) ) m \geq ploy\left( \frac{1}{\epsilon},\frac{1}{\delta}{,size\left( x \right),size\left( c \right)} \right) m≥ploy(ϵ1,δ1,size(x),size(c))中最小的m,称为学习算法 L \mathcal{L} L的样本复杂度
12.3 有限假设空间
12.3.1 可分情形
可分情形:目标概念c属于假设空间 H \mathcal{H} H
假设h的泛化误差大于 ϵ \epsilon ϵ,对分布 D \mathcal{D} D上随机采样的任何样例 ( x , y ) \left( x,y \right) (x,y)
P ( h ( x ) = y ) = 1 − P ( h ( x ) ≠ y ) = 1 − E ( h ) < 1 − ϵ P\left( h\left( x \right) = y \right) = 1 - P\left( h\left( x \right) \neq y \right) = 1 - E\left( h \right) < 1 - \epsilon P(h(x)=y)=1−P(h(x)̸=y)=1−E(h)<1−ϵ
由于D包含m个从 D \mathcal{D} D独立同分布采样而得的样例,h与D表现一致的概率为
P ( ( h ( x 1 ) = y 1 ) ∧ … ∧ ( h ( x m ) = y m ) ) = ( 1 − P ( ( h ( x ) ≠ y ) ) ) m < ( 1 − ϵ ) m P\left( \left( h\left( x_{1} \right) = y_{1} \right) \land \ldots \land \left( h\left( x_{m} \right) = y_{m} \right) \right) = \left( 1 - P\left( \left( h\left( x \right) \neq y \right) \right) \right)^{m} < \left( 1 - \epsilon \right)^{m} P((h(x1)=y1)∧…∧(h(xm)=ym))=(1−P((h(x)̸=y)))m<(1−ϵ)m
仅需保证泛化误差大于 ϵ \epsilon ϵ,且在训练集上表现完美的所有假设出现概率之和不大于 δ \delta δ:
P ( h ∈ H : E ( h ) > ϵ ∧ E ^ ( h ) = 0 ) < ∣ H ∣ ( 1 − ϵ ) m < ∣ H ∣ e − m ϵ P\left( h \in \mathcal{H:}E\left( h \right) > \epsilon \land \hat{E}\left( h \right) = 0 \right) < \left| \mathcal{H} \right|\left( 1 - \epsilon \right)^{m} < \left| \mathcal{H} \right|e^{- m\epsilon} P(h∈H:E(h)>ϵ∧E^(h)=0)<∣H∣(1−ϵ)m<∣H∣e−mϵ
令上式不大于 δ \delta δ,即
∣ H ∣ e − m ϵ ≤ δ \left| \mathcal{H} \right|e^{- m\epsilon} \leq \delta ∣H∣e−mϵ≤δ
得
m ≥ 1 ϵ ( ln ∣ H ∣ + ln 1 δ ) m \geq \frac{1}{\epsilon}\left( \ln{\left| \mathcal{H} \right| + \ln\frac{1}{\delta}} \right) m≥ϵ1(ln∣H∣+lnδ1)
12.3.2 不可分情形
不可分情形:目标概念c不属于假设空间 H \mathcal{H} H
若训练集D包含m个从分布 D \mathcal{D} D上独立同分布采样而得的样例, 0 < ϵ < 1 0 < \epsilon < 1 0<ϵ<1,则对任意 h ∈ H h\mathcal{\in H} h∈H,有
P ( E ^ ( h ) − E ( h ) ≥ ϵ ) ≤ e x p ( − 2 m ϵ 2 ) P\left( \hat{E}\left( h \right) - E\left( h \right) \geq \epsilon \right) \leq exp\left( - 2m\epsilon^{2} \right) P(E^(h)−E(h)≥ϵ)≤exp(−2mϵ2)
P ( E ( h ) − E ^ ( h ) ≥ ϵ ) ≤ e x p ( − 2 m ϵ 2 ) P\left( E\left( h \right) - \hat{E}\left( h \right) \geq \epsilon \right) \leq exp\left( - 2m\epsilon^{2} \right) P(E(h)−E^(h)≥ϵ)≤exp(−2mϵ2)
P ( ∣ E ( h ) − E ^ ( h ) ∣ ≥ ϵ ) ≤ 2 e x p ( − 2 m ϵ 2 ) P\left( \left| E\left( h \right) - \hat{E}\left( h \right) \right| \geq \epsilon \right) \leq 2exp\left( - 2m\epsilon^{2} \right) P(∣∣∣E(h)−E^(h)∣∣∣≥ϵ)≤2exp(−2mϵ2)
若训练集D包含m个从分布 D \mathcal{D} D上独立同分布采样而得的样例, 0 < ϵ < 1 0 < \epsilon < 1 0<ϵ<1,则对任意 h ∈ H h\mathcal{\in H} h∈H,则以 1 − δ 1 - \delta 1−δ的概率成立
E ^ ( h ) − ln ( 2 δ ) 2 m ≤ E ( h ) ≤ E ^ ( h ) + ln ( 2 δ ) 2 m \hat{E}\left( h \right) - \sqrt{\frac{\ln\left( \frac{2}{\delta} \right)}{2m}} \leq E\left( h \right) \leq \hat{E}\left( h \right) + \sqrt{\frac{\ln\left( \frac{2}{\delta} \right)}{2m}} E^(h)−2mln(δ2)≤E(h)≤E^(h)+2mln(δ2)
上式表明,样例数目m较大时,h的经验误差是其泛化误差很好的近似。
若 H \mathcal{H} H为有限假设空间, 0 < δ < 1 0 < \delta < 1 0<δ<1,则对任意 h ∈ H h\mathcal{\in H} h∈H,有
P ( ∣ E ( h ) − E ^ ( h ) ∣ ≤ ln ∣ H ∣ + ln ( 2 δ ) 2 m ) ≥ 1 − δ P\left( \left| E\left( h \right) - \hat{E}\left( h \right) \right| \leq \sqrt{\frac{\ln{\left| \mathcal{H} \right| + \ln\left( \frac{2}{\delta} \right)}}{2m}} \right) \geq 1 - \delta P⎝⎛∣∣∣E(h)−E^(h)∣∣∣≤2mln∣H∣+ln(δ2)⎠⎞≥1−δ
不可知PAC可学习(agnostic PAC learnable):令m表示从分布 D \mathcal{D} D上独立同分布采样而得的样例数目, 0 < ϵ , δ < 1 0 <\epsilon,\delta <1 0<ϵ,δ<1,对所所有分布 D \mathcal{D} D,若存在学习算法 L \mathcal{L} L和多项式函数 poly ( . , . , . ) \text{poly}\left(.,.,. \right) poly(.,.,.),使得对于任何 m ≥ p l o y ( 1 ϵ , 1 δ , s i z e ( x ) , s i z e ( c ) ) m \geq ploy\left( \frac{1}{\epsilon},\frac{1}{\delta}{,size\left( x \right),size\left( c \right)} \right) m≥ploy(ϵ1,δ1,size(x),size(c)), L \mathcal{L} L能从假设空间 H \mathcal{H} H中输出满足下式的假设h:

则称假设空间 H \mathcal{H} H是不可知PAC可学习的
12.4 VC维
给定假设空间 H \mathcal{H} H和示例集 D = { x 1 , x 2 , … , x m } D = \left\{ x_{1},x_{2},\ldots,x_{m} \right\} D={x1,x2,…,xm}, H \mathcal{H} H中每个假设h都能对D中示例赋予标记,标记结果可表示为
h ∣ D = { ( h ( x 1 ) , h ( x 2 ) , … , h ( x m ) ) } {h|}_{D} = \left\{ \left( h\left( x_{1} \right),h\left( x_{2} \right),\ldots,h\left( x_{m} \right) \right) \right\} h∣D={(h(x1),h(x2),…,h(xm))}
随着m的增大, H \mathcal{H} H中所有假设对D中的示例所能赋予标记的可能结果数也会增大
对所有 m ∈ N m \in \mathcal{N} m∈N,假设空间 H \mathcal{H} H的增长函数(growth function) Π H ( m ) \Pi_{\mathcal{H}}\left( m \right) ΠH(m)为
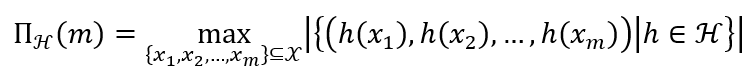
对假设空间 H , m ∈ N , 0 < ϵ < 1 \mathcal{H},m \in \mathbb{N},0 < \epsilon < 1 H,m∈N,0<ϵ<1和任意 h ∈ H h \in \mathcal{H} h∈H有
P ( ∣ E ( h ) − E ^ ( h ) ∣ > ϵ ) ≤ 4 Π H ( 2 m ) exp ( − m ϵ 2 8 ) P\left( \left| E\left( h \right) - \hat{E}\left( h \right) \right| > \epsilon \right) \leq 4\Pi_{\mathcal{H}}\left( 2m \right)\exp\left( - \frac{m\epsilon^{2}}{8} \right) P(∣∣∣E(h)−E^(h)∣∣∣>ϵ)≤4ΠH(2m)exp(−8mϵ2)
假设空间 H \mathcal{H} H的VC维是能被 H \mathcal{H} H打散的最大示例集的大小,即
VC ( H ) = m a x { m : Π H ( m ) = 2 m } \text{VC}\left( \mathcal{H} \right) = max\left\{ m:\Pi_{\mathcal{H}}\left( m \right) = 2^{m} \right\} VC(H)=max{m:ΠH(m)=2m}
若假设空间 H \mathcal{H} H的VC维为d,则对任意 m ∈ N m\mathbb{\in N} m∈N有
Π H ( m ) ≤ ∑ i = 1 d ( m i ) \Pi_{\mathcal{H}}\left( m \right) \leq \sum_{i = 1}^{d}\left( \frac{m}{i} \right) ΠH(m)≤i=1∑d(im)
若假设空间 H \mathcal{H} H的VC维为d,则对任意 m ≥ d m \geq d m≥d有
Π H ( m ) ≤ ( e ∗ m d ) d \Pi_{\mathcal{H}}\left( m \right) \leq \left( \frac{e*m}{d} \right)^{d} ΠH(m)≤(de∗m)d
若假设空间 H \mathcal{H} H的VC维为d,则对任意 m > d , 0 < δ < 1 m > d,0 < \delta < 1 m>d,0<δ<1 和 和 和 h ∈ H h \in \mathcal{H} h∈H有
P ( ∣ E ( h ) − E ^ ( h ) ∣ ≤ 8 d ln 2 e m d + 8 ln 4 δ m ) ≥ 1 − δ P\left( \left| E\left( h \right) - \hat{E}\left( h \right) \right| \leq \sqrt{\frac{8d\ln{\frac{2em}{d} + 8\ln\frac{4}{\delta}}}{m}} \right) \geq 1 - \delta P⎝⎛∣∣∣E(h)−E^(h)∣∣∣≤m8dlnd2em+8lnδ4⎠⎞≥1−δ
任何VC维有限的假设空间 H \mathcal{H} H都是(不可知)PAC可学习的
12.5 Rademacher复杂度
Rademacher复杂度(Rademacher complexity)是另一种刻画假设空间复杂度的途径,在一定程度上考虑数据分布。
给定训练集 D = { ( x 1 , y 1 ) , ( x 2 , y 2 ) , … , ( x m , y m ) } D = \left\{ \left( x_{1},y_{1} \right),\left( x_{2},y_{2} \right),\ldots,\left( x_{m},y_{m} \right) \right\} D={(x1,y1),(x2,y2),…,(xm,ym)},假设h的经验误差为
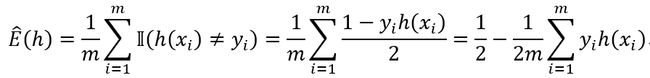
其中 1 m ∑ i = 1 m y i h ( x i ) \frac{1}{m}\sum_{i = 1}^{m}{y_{i}h\left( x_{i} \right)} m1∑i=1myih(xi)体现了预测值 h ( x i ) h\left( x_{i} \right) h(xi)与样例真实标记 y i y_{i} yi之间的一致性,若对于所有 i ∈ { 1 , 2 , … , m } i \in \left\{ 1,2,\ldots,m \right\} i∈{1,2,…,m}都有 h ( x i ) = y i h\left( x_{i} \right) = y_{i} h(xi)=yi,则 1 m ∑ i = 1 m y i h ( x i ) \frac{1}{m}\sum_{i = 1}^{m}{y_{i}h\left( x_{i} \right)} m1∑i=1myih(xi)取最大值1,误差经验最小的假设是
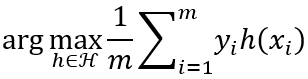
考虑随机变量 σ i \sigma_{i} σi,以0.5的概率取值-1,0.5的概率取值+1,称为Rademacher随机变量。基于 σ i \sigma_{i} σi的重写为

则上式取得的期望为
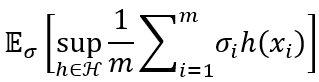
其中 σ = { σ 1 , σ 2 , … , σ m } \sigma = \left\{ \sigma_{1},\sigma_{2},\ldots,\sigma_{m} \right\} σ={σ1,σ2,…,σm}
考虑实值函数空间 F : Z → R \mathcal{F:Z}\mathbb{\rightarrow R} F:Z→R。令 Z = { z 1 , z 2 , … , z m } Z = \left\{ z_{1},z_{2},\ldots,z_{m} \right\} Z={z1,z2,…,zm},其中 z i ∈ Z z_{i}\mathcal{\in Z} zi∈Z,函数空间 F \mathcal{F} F关于 Z \mathcal{Z} Z的经验Rademacher复杂度
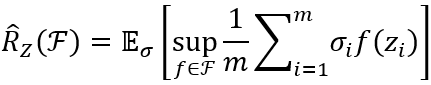
函数空间 F \mathcal{F} F关于 Z \mathcal{Z} Z上分布 D \mathcal{D} D的Rademacher复杂度
R m ( F ) = E Z ⊆ Z : ∣ Z ∣ = m [ R ^ Z ( F ) ] R_{m}\left( \mathcal{F} \right) = \mathbb{E}_{Z \subseteq \mathcal{Z:}\left| Z \right| = m}\left\lbrack {\hat{R}}_{Z}\left( \mathcal{F} \right) \right\rbrack Rm(F)=EZ⊆Z:∣Z∣=m[R^Z(F)]
基于Rademacher复杂度可得关于函数空间 F \mathcal{F} F的泛化误差界
对实值函数空间 F : Z → [ 0 , 1 ] \mathcal{F:Z \rightarrow}\left\lbrack 0,1 \right\rbrack F:Z→[0,1],根据分布 D \mathcal{D} D从 Z \mathcal{Z} Z中独立分布采样得到示例集 Z = { z 1 , z 2 , … , z m } , z i ∈ Z , 0 < δ < 1 Z = \left\{ z_{1},z_{2},\ldots,z_{m} \right\},z_{i}\mathcal{\in Z},0 < \delta < 1 Z={z1,z2,…,zm},zi∈Z,0<δ<1,对任意 f ∈ F f\mathcal{\in F} f∈F,以至少 1 − δ 1 - \delta 1−δ的概率有
E [ f ( z ) ] ≤ 1 m ∑ i = 1 m f ( z i ) + 2 R m ( F ) + ln ( 1 δ ) 2 m \mathbb{E}\left\lbrack f\left( z \right) \right\rbrack \leq \frac{1}{m}\sum_{i = 1}^{m}{f\left( z_{i} \right) + 2R_{m}\left( \mathcal{F} \right) + \sqrt{\frac{\ln\left( \frac{1}{\delta} \right)}{2m}}} E[f(z)]≤m1i=1∑mf(zi)+2Rm(F)+2mln(δ1)
E [ f ( z ) ] ≤ 1 m ∑ i = 1 m f ( z i ) + 2 R ^ Z ( F ) + 3 ln ( 2 δ ) 2 m \mathbb{E}\left\lbrack f\left( z \right) \right\rbrack \leq \frac{1}{m}\sum_{i = 1}^{m}{f\left( z_{i} \right) + 2{\hat{R}}_{Z}\left( \mathcal{F} \right) + 3\sqrt{\frac{\ln\left( \frac{2}{\delta} \right)}{2m}}} E[f(z)]≤m1i=1∑mf(zi)+2R^Z(F)+32mln(δ2)
对假设空间 H : X → { − 1 , + 1 } \mathcal{H:X \rightarrow}\left\{ - 1, + 1 \right\} H:X→{−1,+1},根据分布 D \mathcal{D} D从 X \mathcal{X} X中独立分布采样得到示例集 D = { x 1 , x 2 , … , x m } , x i ∈ X , 0 < δ < 1 D = \left\{ x_{1},x_{2},\ldots,x_{m} \right\},x_{i}\mathcal{\in X},0 < \delta < 1 D={x1,x2,…,xm},xi∈X,0<δ<1,对任意 h ∈ H h\mathcal{\in H} h∈H,以至少 1 − δ 1 - \delta 1−δ的概率有
E ( h ) ≤ E ^ ( h ) + R m ( h ) + ln ( 1 δ ) 2 m \mathbb{E}\left( h \right) \leq \hat{E}\left( h \right) + R_{m}\left( h \right) + \sqrt{\frac{\ln\left( \frac{1}{\delta} \right)}{2m}} E(h)≤E^(h)+Rm(h)+2mln(δ1)
E ( h ) ≤ E ^ ( h ) + R ^ D ( h ) + 3 ln ( 1 δ ) 2 m \mathbb{E}\left( h \right) \leq \hat{E}\left( h \right) + {\hat{R}}_{D}\left( h \right) + 3\sqrt{\frac{\ln\left( \frac{1}{\delta} \right)}{2m}} E(h)≤E^(h)+R^D(h)+32mln(δ1)
假设空间 H \mathcal{H} H的Rademacher复杂度 R m ( H ) R_{m}\left( \mathcal{H} \right) Rm(H)与增长函数 Π H ( m ) \Pi_{\mathcal{H}}\left( m \right) ΠH(m)满足
R m ( H ) ≤ 2 ln Π H ( m ) m R_{m}\left( \mathcal{H} \right) \leq \sqrt{\frac{2\ln{\Pi_{\mathcal{H}}\left( m \right)}}{m}} Rm(H)≤m2lnΠH(m)
则
E ( h ) ≤ E ^ ( h ) + 2 d ln em d m + ln ( 1 δ ) 2 m E\left( h \right) \leq \hat{E}\left( h \right) + \sqrt{\frac{2d\ln\frac{\text{em}}{d}}{m}} + \sqrt{\frac{\ln\left( \frac{1}{\delta} \right)}{2m}} E(h)≤E^(h)+m2dlndem+2mln(δ1)
12.6 稳定性
算法的稳定性考察的是算法在输入发生变化时,输出是否会随之发生较大的变化。
给定 D = { z 1 = ( x 1 , y 1 ) , z 2 = ( x 2 , y 2 ) , … , z m = ( x m , y m ) } , x i ∈ X D = \left\{ z_{1} = \left( x_{1},y_{1} \right),z_{2} = \left( x_{2},y_{2} \right),\ldots,z_{m} = \left( x_{m},y_{m} \right) \right\},x_{i}\mathcal{\in X} D={z1=(x1,y1),z2=(x2,y2),…,zm=(xm,ym)},xi∈X是来自分布 D \mathcal{D} D的独立同分布示例, y i = { − 1 , + 1 } y_{i} = \left\{ - 1, + 1 \right\} yi={−1,+1}。对假设空间 H : X → { − 1 , + 1 } \mathcal{H:X \rightarrow}\left\{ - 1, + 1 \right\} H:X→{−1,+1}和学习算法 L \mathcal{L} L,令 L D ∈ H \mathcal{L}_{D}\mathcal{\in H} LD∈H表示基于训练集D从假设空间 H \mathcal{H} H中学得的假设。
D \ i D^{\backslash i} D\i表示移除D中第i个样例得到的集合
D \ i = { z 1 , z 2 , … , z i − 1 , z i + 1 , … , z m } D^{\backslash i} = \left\{ z_{1},z_{2},\ldots,z_{i - 1},z_{i + 1},\ldots,z_{m} \right\} D\i={z1,z2,…,zi−1,zi+1,…,zm}
D i D^{i} Di表示替换D中第i个样例得到的集合
D \ i = { z 1 , z 2 , … , z i − 1 , z i ′ , z i + 1 , … , z m } D^{\backslash i} = \left\{ z_{1},z_{2},\ldots,z_{i - 1},{z_{i}^{'},z}_{i + 1},\ldots,z_{m} \right\} D\i={z1,z2,…,zi−1,zi′,zi+1,…,zm}
其中 z i ′ = ( x i ′ , y i ′ ) , x i ′ z_{i}^{'} = \left( x_{i}^{'},y_{i}^{'} \right),x_{i}^{'} zi′=(xi′,yi′),xi′服从分布 D \mathcal{D} D并独立于D
损失函数 l ( L D ( x ) , y ) : Y × Y → R + \mathcal{l}\left( \mathcal{L}_{D}\left( x \right),y \right)\mathcal{:Y \times Y \rightarrow}\mathbb{R}^{+} l(LD(x),y):Y×Y→R+刻画了假设 L D \mathcal{L}_{D} LD的预测标记 L D ( x ) \mathcal{L}_{D}\left( x \right) LD(x)与真实标记y之间的差别,简记 l ( L D , z ) \mathcal{l}\left( \mathcal{L}_{D},z \right) l(LD,z),则
泛化损失
l ( L , D ) = E x ∈ X , z = ( x , y ) [ l ( L D , z ) ] \mathcal{l}\left( \mathcal{L,D} \right) = \mathbb{E}_{x \in \mathcal{X,}z = \left( x,y \right)}\left\lbrack \mathcal{l}\left( \mathcal{L}_{D},z \right) \right\rbrack l(L,D)=Ex∈X,z=(x,y)[l(LD,z)]
经验损失
l ^ ( L , D ) = 1 m ∑ i = 1 m l ( L D , z i ) \hat{\mathcal{l}}\left( \mathcal{L,D} \right) = \frac{1}{m}\sum_{i = 1}^{m}{\mathcal{l}\left( \mathcal{L}_{D},z_{i} \right)} l^(L,D)=m1i=1∑ml(LD,zi)
留一(leave-one-out)损失
l loo ( L , D ) = 1 m ∑ i = 1 m l ( L D \ i , z i ) \mathcal{l}_{\text{loo}}\left( \mathcal{L,D} \right) = \frac{1}{m}\sum_{i = 1}^{m}{\mathcal{l}\left( \mathcal{L}_{D^{\backslash i}},z_{i} \right)} lloo(L,D)=m1i=1∑ml(LD\i,zi)
对任意 x ∈ X , z = ( x , y ) x \in \mathcal{X,}z = \left( x,y \right) x∈X,z=(x,y),若学习算法 L \mathcal{L} L满足 ∣ l ( L D , z ) − l ( L D \ i , z ) ∣ ≤ β , i = 1 , 2 , … , m \left| \mathcal{l}\left( \mathcal{L}_{D},z \right) - \mathcal{l}\left( \mathcal{L}_{D^{\backslash i}},z \right) \right| \leq \beta,i =1,2,\ldots,m ∣l(LD,z)−l(LD\i,z)∣≤β,i=1,2,…,m,则称 L \mathcal{L} L关于损失函数 l \mathcal{l} l满足 β \beta β-均匀稳定性。
则
∣ l ( L D , z ) − l ( L D \ i , z ) ∣ ≤ ∣ l ( L D , z ) − l ( L D \ i , z ) ∣ + ∣ l ( L D i , z ) − l ( L D \ i , z ) ∣ ≤ 2 β \left| \mathcal{l}\left( \mathcal{L}_{D},z \right) - \mathcal{l}\left( \mathcal{L}_{D^{\backslash i}},z \right) \right| \leq \left| \mathcal{l}\left( \mathcal{L}_{D},z \right) - \mathcal{l}\left( \mathcal{L}_{D^{\backslash i}},z \right) \right| + \left| \mathcal{l}\left( \mathcal{L}_{D^{i}},z \right) - \mathcal{l}\left( \mathcal{L}_{D^{\backslash i}},z \right) \right| \leq 2\beta ∣l(LD,z)−l(LD\i,z)∣≤∣l(LD,z)−l(LD\i,z)∣+∣l(LDi,z)−l(LD\i,z)∣≤2β
若损失函数 l \mathcal{l} l有界,即对所有D和 z = ( x , y ) z = \left( x,y \right) z=(x,y)有 0 ≤ l ( L D , z ) ≤ M 0\mathcal{\leq l}\left( \mathcal{L}_{D},z \right) \leq M 0≤l(LD,z)≤M,则有:
给定分布 D \mathcal{D} D上独立同分布采样得到的大小为m的示例集D,若学习算法 L \mathcal{L} L满足关于损失函数 l \mathcal{l} l满足 β \beta β-均匀稳定性,且损失函数 l \mathcal{l} l的上界为 M , 0 < δ < 1 M,0< \delta < 1 M,0<δ<1,则对任意 m ≥ 1 m \geq 1 m≥1,以至少 1 − δ 1 - \delta 1−δ的概率有
l ( L , D ) ≤ l ^ ( L , D ) + 2 β + ( 4 m β + M ) ln ( 1 δ ) 2 m \mathcal{l}\left( \mathcal{L,D} \right) \leq \hat{\mathcal{l}}\left( \mathcal{L,D} \right) + 2\beta + \left( 4m\beta + M \right)\sqrt{\frac{\ln\left( \frac{1}{\delta} \right)}{2m}} l(L,D)≤l^(L,D)+2β+(4mβ+M)2mln(δ1)
l ( L , D ) ≤ l loo ( L , D ) + β + ( 4 m β + M ) ln ( 1 δ ) 2 m \mathcal{l}\left( \mathcal{L,D} \right) \leq \mathcal{l}_{\text{loo}}\left( \mathcal{L,D} \right) + \beta + \left( 4m\beta + M \right)\sqrt{\frac{\ln\left( \frac{1}{\delta} \right)}{2m}} l(L,D)≤lloo(L,D)+β+(4mβ+M)2mln(δ1)
对损失函数 l \mathcal{l} l,若学习算法 L \mathcal{L} L满足经验风险最小化(Empirical Risk Minimization)原则,简称算法是ERM的
若学习算法 L \mathcal{L} L是ERM且稳定的,则假设空间 H \mathcal{H} H可学习。