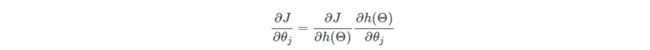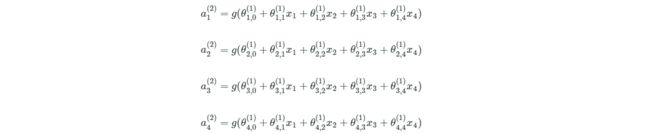鸢尾花分类——神经网络详解

神经元的广泛互联与并行工作必然使整个网络呈现出高度的非线性特点。在客观世界中，许多系统的输入与输出之间存在着复杂的非线性关系，对于这类系统，往往很难用传统的数理方法建立其数学模型。设计合理地神经网络通过对系统输入输出样本对进行自动学习，能够以任意精度逼近任何复杂的非线性映射。神经网络的这一优点能使其可以作为多维非线性函数的通用数学模型。该模型的表达式非解析的，输入输出数据之间的映射规则由神经网络在学习阶段自动抽取并分布式存储在网络的所有连接中。具有非线性映射功能的神经网络应用十分广阔，几乎涉及所有领域。

Dataset

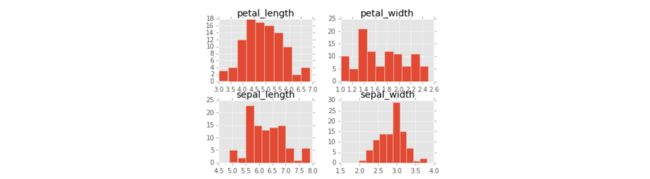
本文的数据集是常见的官方数据集鸢尾花iris.csv，该数据集的特征如下：

• sepal_length - Continuous variable measured in centimeters.
• sepal_width - Continuous variable measured in centimeters.
• petal_length - Continuous variable measured in centimeters.
• petal_width - Continuous variable measured in centimeters.
• species - Categorical. 2 species of iris flowers, Iris-virginica or
  Iris-versicolor.

import pandas
import matplotlib.pyplot as plt
import numpy as np
iris = pandas.read_csv("iris.csv")
# shuffle rows
shuffled_rows = np.random.permutation(iris.index)
iris = iris.loc[shuffled_rows,:]
print(iris.head())
'''
    sepal_length  sepal_width  petal_length  petal_width          species
80           7.4          2.8           6.1          1.9   Iris-virginica
84           6.1          2.6           5.6          1.4   Iris-virginica
33           6.0          2.7           5.1          1.6  Iris-versicolor
81           7.9          3.8           6.4          2.0   Iris-virginica
93           6.8          3.2           5.9          2.3   Iris-virginica
'''
# There are 2 species
print(iris.species.unique())
'''
['Iris-virginica' 'Iris-versicolor']
'''
iris.hist()
plt.show()

• 下面是数据集的每个特征取值的分布。

  

Neurons

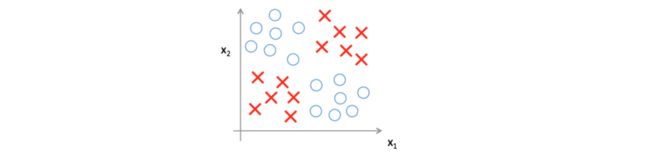
• 目前为止，我们讨论的问题都是线性的，比如在二维例子里能找到一条曲线将数据纯净的分离开。但是，有的数据线性不可分的，比如：

  

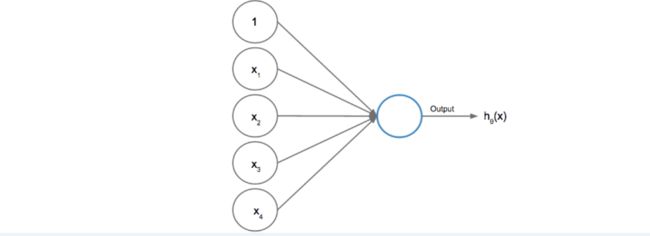
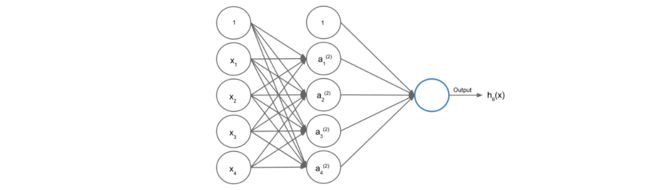
• 无论是线性回归还是逻辑回归都无法建立这样一个函数可以将这个数据分离开，因此必须采用神经网络这样的可以处理非线性数据的模型。这些模型是由一系列神经元组成,然后输出预测的结果。神经元接受一些输入,应用一个转换函数,并返回一个输出。下面我们看看一个神经元的例子，其中输入为5个值，一个偏差单元（类似线性模型中的截距），4个特征。

  

• 这些单元进入到激活函数h里面。我们可以用一个逻辑激活函数g将这些输入转化为一个0到1之间的概率值输出，可以发现前面学习的逻辑回归函数是可以用作这里的一个神经元的。：

  
  

• 下面这段代码：将样本的第一行输入到神经元中，激活函数是逻辑函数，权值为随机，打印输出：

# 添加一个值全为1的属性iris["ones"]，截距
iris["ones"] = np.ones(iris.shape[0])
X = iris[['ones', 'sepal_length', 'sepal_width', 'petal_length', 'petal_width']].values
# 将Iris-versicolor类标签设置为1，Iris-virginica设置为0
y = (iris.species == 'Iris-versicolor').values.astype(int) 

# The first observation
x0 = X[0]

# 随机初始化一个系数列向量
theta_init = np.random.normal(0,0.01,size=(5,1))
def sigmoid_activation(x, theta):
    x = np.asarray(x)
    theta = np.asarray(theta)
    return 1 / (1 + np.exp(-np.dot(theta.T, x)))

a1 = sigmoid_activation(x0, theta_init)
print(a1)
'''
[ 0.47681073]
'''

Cost Function

• 误差函数定义如下（其中yi是真实值，h(xi)是预测值）：当yi=1时，h(xi)接近1，那么log(h(xi))就接近0，表示误差几乎为0。由于这个log()函数的值都是负的，为了使这个值为正，在前面加了一个负号，那么变为求J(Θ)的最大化，在梯度下降那里，应该是加上而不是减去。：
  

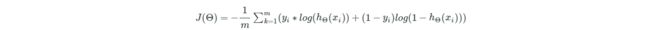
• 计算一个样本的误差：

# First observation's features and target
x0 = X[0]
y0 = y[0]

theta_init = np.random.normal(0,0.01,size=(5,1))
def singlecost(X, y, theta):
    # Compute activation
    h = sigmoid_activation(X.T, theta)
    # Take the negative average of target*log(activation) + (1-target) * log(1-activation)
    cost = -np.mean(y * np.log(h) + (1-y) * np.log(1-h))
    return cost

first_cost = singlecost(x0, y0, theta_init)
'''
0.64781198784027283
'''

Compute The Gradients

• 在利用梯度下降迭法求参数最优时，我们需要计算损失函数关于参数的偏导，由于此时的误差函数是激活函数的函数，因此求偏导略微有些复杂：

  

• 最终推导的结果如下，其中(yi−hΘ(xi))∗hΘ(xi)∗(1−hΘ(xi))是标量，而xi是向量，因此δ是行向量：

  

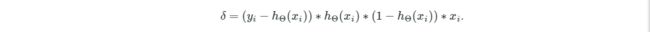
• 神经网络是每次输入一个样本，然后计算每个样本产生的误差的偏导δi，最后计算这些δi向量的 平均值向量来更新参数:

# Initialize parameters
theta_init = np.random.normal(0,0.01,size=(5,1))

# Store the updates into this array
grads = np.zeros(theta_init.shape) # (5,1)

# Number of observations 
n = X.shape[0]
for j, obs in enumerate(X):
    # 计算预测值h(xi)
    h = sigmoid_activation(obs, theta_init)
    # 计算参数偏导δi
    delta = (y[j]-h) * h * (1-h) * obs
    # 对δi求平均
    grads += delta[:,np.newaxis]/X.shape[0]
print(grads)
'''
[[ 0.00473195]
 [-0.01063693]
 [ 0.00099274]
 [-0.05689875]
 [-0.03557351]]
'''

Two Layer Network

• 上面计算了参数的偏导后，需要岁原来的参数进行调整，将原参数 - 梯度*学习率。在下面这段代码中，通过这个learn函数我们学习到一个收敛的参数：参数为样本数据，学习率，初始参数，最大迭代次数，阈值。

theta_init = np.random.normal(0,0.01,size=(5,1))

# set a learning rate
learning_rate = 0.1
# maximum number of iterations for gradient descent
maxepochs = 10000       
# costs convergence threshold, ie. (prevcost - cost) > convergence_thres
convergence_thres = 0.0001  

def learn(X, y, theta, learning_rate, maxepochs, convergence_thres):
    costs = []
    # 计算一个样本产生的误差损失
    cost = singlecost(X, y, theta) 
    # 0.01+阈值是为了在第一次迭代后与前一次（初始化为第一个样本的误差）误差的差值大于阈值
    costprev = cost + convergence_thres + 0.01  
    counter = 0 
    for counter in range(maxepochs):
        grads = np.zeros(theta.shape) # 初始化梯度为全0向量
        for j, obs in enumerate(X): # for循环计算总样本的平均梯度
            h = sigmoid_activation(obs, theta)   
            delta = (y[j]-h) * h * (1-h) * obs  
            grads += delta[:,np.newaxis]/X.shape[0]  
        # 更新参数，由于J(Θ)前面加了负号，因此求最大值，所有此处是+
        theta += grads * learning_rate
        counter += 1 
        costprev = cost  # 存储前一次迭代产生的误差
        cost = singlecost(X, y, theta) # compute new cost
        costs.append(cost)
        if np.abs(costprev-cost) < convergence_thres: # 两次迭代误差大于阈值退出
            break

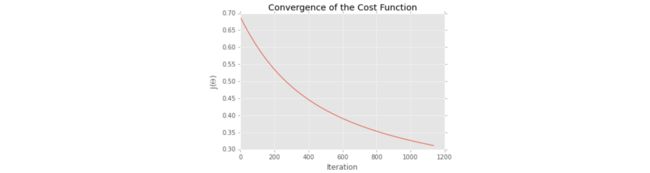
    plt.plot(costs)
    plt.title("Convergence of the Cost Function")
    plt.ylabel("J($\Theta$)")
    plt.xlabel("Iteration")
    plt.show()
    return theta

theta = learn(X, y, theta_init, learning_rate, maxepochs, convergence_thres)

Neural Network

• 神经网络通常有很多层，最简单的是三层结构：输入层，中间层以及输出层。

  

• 中间层神经元的值计算公式如下，其中θ参数是每条边上的权值：

  

• 最终的输出如下，其中θ0是中间层的截距：

  

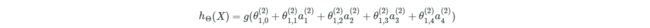
• 下面是计算中间层a1的值，其中theta0_init是输入层到中间层的权值，theta1_init是中间层到输出层的权值。

theta0_init = np.random.normal(0,0.01,size=(5,4))
theta1_init = np.random.normal(0,0.01,size=(5,1))
# sigmoid_activation函数是前面已经写好的，在这作参考
def sigmoid_activation(x, theta):
    x = np.asarray(x)
    theta = np.asarray(theta)
    return 1 / (1 + np.exp(-np.dot(theta.T, x)))
def feedforward(X, theta0, theta1):
    # 逻辑函数中X.T(5,N), theta0(5,4)->(4,N)
    a = sigmoid_activation(X.T, theta0).T
    # a中每一行是一个样本产生的中间层的四个输入
    # 添加一个列值为1的截距向量
    # column_stack将将行数相同的两个数组纵向合并
    a = np.column_stack([np.ones(a.shape[0]), a])
    # activation units are then inputted to the output layer
    out = sigmoid_activation(a.T, theta1)
    return out

h = feedforward(X, theta0_init, theta1_init)

Multiple Neural Network Cost Function

• 多层神经网络的误差计算公式如下，同样由于加了负号，变为求最大值：

  

theta0_init = np.random.normal(0,0.01,size=(5,4))
theta1_init = np.random.normal(0,0.01,size=(5,1))

# X and y are in memory and should be used as inputs to multiplecost()
def multiplecost(X, y, theta0, theta1):
    # feed through network
    h = feedforward(X, theta0, theta1) 
    # compute error
    inner = y * np.log(h) + (1-y) * np.log(1-h)
    # negative of average error
    return -np.mean(inner)

c = multiplecost(X, y, theta0_init, theta1_init)

Backpropagation

• 前面我们初始化了参数，利用前向传播（forward propagation）得到了所有样本产生的输出从而得到误差值。现在要学习一个模型来修改前面的参数，使得J(Θ)最大化（误差最小化）。我们利用反向传播（Back propagation）从最后一层绕回到最开始的一层来逐层修改参数。
• 同样的我们还是要计算误差函数关于参数的偏导，其中l为神经网络的层数：
  

• 对于一个三层的神经网络，梯度计算如下：
  

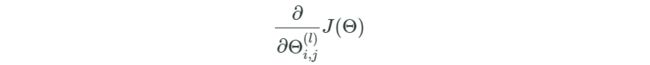
• 下面是三层神经网络的完整代码：

# 将模型的函数凝结为一个类，这是很好的一种编程习惯
class NNet3:
    # 初始化必要的几个参数
    def __init__(self, learning_rate=0.5, maxepochs=1e4, convergence_thres=1e-5, hidden_layer=4):
        self.learning_rate = learning_rate
        self.maxepochs = int(maxepochs)
        self.convergence_thres = 1e-5
        self.hidden_layer = int(hidden_layer)

    #  计算最终的误差  
    def _multiplecost(self, X, y):
        # l1是中间层的输出，l2是输出层的结果
        l1, l2 = self._feedforward(X) 
        # 计算误差，这里的l2是前面的h
        inner = y * np.log(l2) + (1-y) * np.log(1-l2)
        # 添加符号，将其转换为正值
        return -np.mean(inner)

    # 前向传播函数计算每层的输出结果
    def _feedforward(self, X):
        # l1是中间层的输出
        l1 = sigmoid_activation(X.T, self.theta0).T
        # 为中间层添加一个常数列
        l1 = np.column_stack([np.ones(l1.shape[0]), l1])
        # 中间层的输出作为输出层的输入产生结果l2
        l2 = sigmoid_activation(l1.T, self.theta1)
        return l1, l2

    # 传入一个结果未知的样本，返回其属于1的概率
    def predict(self, X):
        _, y = self._feedforward(X)
        return y

    # 学习参数，不断迭代至参数收敛，误差最小化
    def learn(self, X, y):
        nobs, ncols = X.shape
        self.theta0 = np.random.normal(0,0.01,size=(ncols,self.hidden_layer))
        self.theta1 = np.random.normal(0,0.01,size=(self.hidden_layer+1,1))

        self.costs = []
        cost = self._multiplecost(X, y)
        self.costs.append(cost)
        costprev = cost + self.convergence_thres+1  
        counter = 0  

        for counter in range(self.maxepochs):
            # 计算中间层和输出层的输出
            l1, l2 = self._feedforward(X)

            # 首先计算输出层的梯度，再计算中间层的梯度
            l2_delta = (y-l2) * l2 * (1-l2)
            l1_delta = l2_delta.T.dot(self.theta1.T) * l1 * (1-l1)

            # 更新参数
            self.theta1 += l1.T.dot(l2_delta.T) / nobs * self.learning_rate
            self.theta0 += X.T.dot(l1_delta)[:,1:] / nobs * self.learning_rate

            counter += 1  
            costprev = cost 
            cost = self._multiplecost(X, y)  # get next cost
            self.costs.append(cost)
            if np.abs(costprev-cost) < self.convergence_thres and counter > 500:
                break

# Set a learning rate
learning_rate = 0.5
# Maximum number of iterations for gradient descent
maxepochs = 10000       
# Costs convergence threshold, ie. (prevcost - cost) > convergence_thres
convergence_thres = 0.00001  
# Number of hidden units
hidden_units = 4

# Initialize model 
model = NNet3(learning_rate=learning_rate, maxepochs=maxepochs,
              convergence_thres=convergence_thres, hidden_layer=hidden_units)
# Train model
model.learn(X, y)

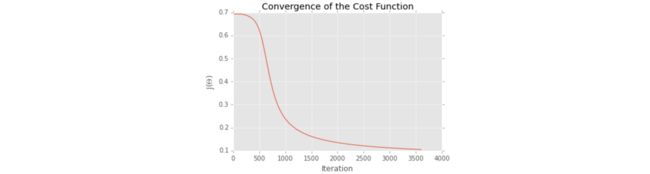
# Plot costs
plt.plot(model.costs)
plt.title("Convergence of the Cost Function")
plt.ylabel("J($\Theta$)")
plt.xlabel("Iteration")
plt.show()

Splitting Data

• 现在已经知道怎么学习一个神经网络，我们需要将数据集划分为训练集和测试集，利用训练集来学习神经网络，利用测试集来检验模型的好坏：

# First 70 rows to X_train and y_train
# Last 30 rows to X_train and y_train
X_train = X[:70]
y_train = y[:70]

X_test = X[-30:]
y_test = y[-30:]

Predicting Iris Flowers

• 进行预测，我们利用AUC值来衡量一个模型的好坏。发现最后的结果是1，表明模型能很好的预测鸢尾花的类别。

from sklearn.metrics import roc_auc_score
# Set a learning rate
learning_rate = 0.5
# Maximum number of iterations for gradient descent
maxepochs = 10000       
# Costs convergence threshold, ie. (prevcost - cost) > convergence_thres
convergence_thres = 0.00001  
# Number of hidden units
hidden_units = 4

# Initialize model 
model = NNet3(learning_rate=learning_rate, maxepochs=maxepochs,
              convergence_thres=convergence_thres, hidden_layer=hidden_units)
model.learn(X_train, y_train)
# 因为predict返回的是一个二维数组，此处是(1,30)，取第一列作为一个列向量
yhat = model.predict(X_test)[0]

auc = roc_auc_score(y_test, yhat)
'''
1.0
'''