[编译原理读书笔记][第3章 词法分析]

[编译原理读书笔记][第3章 词法分析]

标签（空格分隔）： 未分类

---

• 本章我们主要讨论如何构建一个词法分析器

  • 首先建立起每个词法单元的词法结构图或其他描述.
  • 编写代码识别输入中出现的每个词素,并返回识别到词法单元的有关信息

• 词法分析器生成工具(lexical-analyzer generator)

  • 描述出词素模式,然后将这些模式编译为具有词法分析功能的代码.
  • 程序员只要在抽象很高的层次上描述软件,就能生成代码.
  • 3.5节将介绍一个名为Lex分析器生成工具

• 正则表达式

  • 正则表达式是一种很方便描述词素模式的方法.

  • 我们将介绍正则表达式进行转换:

    • 首先转换为不确定有穷自动机.
    • 然后转换为确定又穷自动机.

  • 驱动程序就是模拟这些自动机的代码,使用自动机确定下一个词法单元.

• 驱动程序和自动机的规约形成词法分析器的核心部分.

3.1 词法分析器的作用

词法分析是编译的第一阶段.

• 词法分析器的主要任务是

  • 1.读入源程序的输入字符
  • 2.将他们组成词素,生成并输出一个词法单元序列,每个词法单元对应一个词素.

• 词法分析,语法分析,符号表的交互
  

  • getNextToken所指示的调用使得词法单元从它的输入不断读取字符,直到识别到下一个词素为止.
  • 词法单元根据词生成一个词法单元返回给语法分析.

• 词法分析其余任务

  • 过滤注释和空白
  • 编译器生成的错误信息,和源代码的位置练习起来

• 有时候,词法分析分成两个级联处理

  • 扫描阶段: 不生成词法的单元的简单处理:删除注释和将多个空白压缩成一个
  • 分析极端:处理扫描阶段的输出,返回词法单元

3.1.1 词法分析及语法分析

把编译阶段的分析部分化为词法分析和语法分析阶段有如下几个原因:

• 最重要的考虑是简化编译器设计
• 提高编译器效率(因为能专精)
• 增强编译器的可移植性.

3.1.2 词法单元,模式和词素

三个相关但有区别的术语.

• 词法单元:由一个词法单元名和一个可选属性组成.
  
  • 词法单元名:是一种表示某种词法单元的抽象符号.
    
    • 比如一个关键词,标识符的输入字符序列.
    • 词法单元名是由语法分析处理的输入符号.
    • 通常用黑体字表示词法单元名
• 模式:描述一个词法单元的词素可能具有的形式.
  
  • 词法单元是关键词时:
    
    • 模式是组成这个关键词的字符序列
  • 对于标识符和其他词法单元:
    
    • 模式是一个更加复杂的结构,可以和很多符号串匹配.
  • 正则表达式
• 词素:是源程序的一个字符序列.
  
  • 和某个词法单元的模式匹配
  • 被词法分析器识别为该词法单元的一个实例.

在很多程序设计语言中,下面类别覆盖了大多数词法单元

• 每个关键词有一个词法单元.
  
  • 一个关键词的模式是他本身.
• 表示运算符的词法单元
• 表示所有标识符的词法单元
• 一个或多个表示常量的词法单元
• 每一个标点符号 有一个词法单元

3.1.3 词法单元的属性

• 词法单元的属性:如果多个词素可以和一个模式匹配,那么词法分析器必须向编译器的后续阶段提供被匹配词素的附加信息.
  
  • 一个标识符的属性值是一个指向符号表中该标识符条目的指针.

3.1.4 词法错误

• 如果没有其他组件帮助,词法分析器很难发现源代码的错误.

  比如:

  fi(a==f(x))

  • 词法分析器会当做一个标识符作为词法单元传给语法分析器
  • 这个错误将由语法分析器处理.

• 恐慌模式:所有词法单元都无法和剩余输入的某个前缀相匹配时的策略

  • 我们从剩余的输入不断删除字符,直到词法分析器能够在剩余的开头发现一个正确的词法单元为止.

3.1.5 练习

<float> <id, limitedSquaare> <(> <id, x> <)> <{>
  <float> <id, x>
  <return> <(> <id, x> <op,"<=">  ||"> <id, x> <op, ">="> <num, 10.0> <)> <op, "?"> <num, 100> <op, ":"> <id, x> <op, "*"> <id, x>
<}>

<text, "Here is a photo of"> <nodestart, b> <text, "my house"> <nodeend, b>
<nodestart, p> <selfendnode, img> <selfendnode, br>
<text, "see"> <nodestart, a> <text, "More Picture"> <nodeend, a>
<text, "if you liked that one."> <nodeend, p>

3.2 输入缓冲

讨论几种可以加快源程序读入速度的方法.

• 我们将介绍一种双缓冲区方案
  
  • 这种方案能安全处理向前看多个符号问题.
  • -,=,< 可能是->,==,<=这样双字符运算符的开始.
• 我们将考虑一种改进方法,这种方法用哨兵标记来节约检查缓冲区末端的时间.

3.2.1 缓冲区对

何为缓冲区对?

由于在编译一个大型程序需要处理大量的字符,处理这些字符需要很多时间,由此开发了一些特殊的缓冲技术来减少用于处理单个输入字符的时间开销.一种重要机制是利用两个交替读入的缓冲区.

缓冲区具体

• 每个缓冲区容量都是N个字符,通常N是一块磁盘块大小,如4096字节
• 程序为输入维护了两个指针
  
  • lexemeBegin指针:该指针指向当前词素的开始处.当前我们正试图确定这个词素的结尾.
  • forward指针:它一直向前扫,直到发现某个模式被匹配到为止
    
    • 做出这个决定的策略在之后描述.

• 一旦确定下一个词素,forward指针将指向该词素结尾的字符.

  • 词法分析器将这个词素作为某个词法单元记录下来并返回.
  • 然后使lexemeBegin指针指向刚找到词素后的第一个位置
  • 处理完后,forward指针也会前移一个位置

• 如果forward指针前移超过缓冲区末尾(哨兵标记优化的地方)

  • 将N个新字符读到另一个缓冲区末尾,且将forward指针指向这个新载入符的头部.

3.2.2 哨兵标记

如何优化检测缓冲区末尾呢?

思考之前的有两步操作

• 检查是否到了末尾
• 确定读入的字符

将两步合二为一

在缓冲区末尾扩展一个绝对不会使用的符号,叫做哨兵(sentinel)字符,一个自然的选择是eof.

3.3 词法单元的规约

• 正则表达式是一种用来描述词素模式的重要表示方法.

  • 虽然不能表达所有可能的模式,但能高效描述在处理词法单元时要用到的模式类型.

• 这一节我们将研究正则表达式的形式化表示方法

• 在3.5节中 我们将看到如何将正则表达式用到词法分析生成工具中.

• 在3.7节中 我们将学到如何能将正则表达式转换为能够识别词法单元的自动机,并由此建立一个词法分析树.

3.3.1 串和语言

• 字母表(alphabet)是一个有限的符号集合.

  • 如{0,1},ASCII,Unicode .

• 某个字母表的串(string)是该字母表符号的有穷序列.

• 语言(language)是某个给定字符表上任意的可数的串的集合.

• 字符串的指数运算

  

3.3.2 语言上的运算

在词法分析,最重要的语言上的运算是并,连接,和闭包运算.

3.3.3 正则表达式

• 正则表达式可以由较小的正则表达式按照如下规则递归地构建.

  • 每个正则表达式r表示一个语言L(r),也是根据r的子表达式所构建的语言递归构造.

• 某个字母表Σ上的正则表达式以及这些表达式所表示的语言

  

• 根据优先级丢掉括号

  • 一元运算符*是最高级,并且是左结合.
  • 链接运算符次高的优先级,也是左结合
  • |的游戏级最低,也是左结合.
  • 将 (a)|((b)*(c))改写为a|b*c

• 例子:
  

正则集合

• 可以用同一个正则表达式定义的语言叫做正则集合(regular set)

• 如果两个正则表达式r和s表示的语言相同的语言,则称两者等价,记做r=s.

• 正则表达式遵守一定的代数定律

  

3.3.4 正则定义

• 为方便表示,我们可能希望给某些正则表达式命名,并在之后像使用符号一样使用这些名字,这叫做正则定义(regular definition)是具有如下形式的定义序列:
  
  
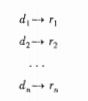
  • 每个di都是一个新符号,不在Σ中,并且各不相同.
  • 每个ri是字母表`Σ U {d1,d2,…di-1}上的正则表达式.

• 可以看出 递归定义是正则表达式的很重要的性质

3.3.5 正则表达式的扩展

除了以上的运算,在现代像Lex这样的实用Unix程序都有对正则的扩展

• 一个或多个实例:+
  
  • 单目后缀运算符+表示一个正则表达式及其语言的正闭包.
  • (r)+ 意思为 (L(r))+
  • +与*有相同的优先级
• 零个或一个实例:?
  
  • 单目后缀运算符?的意思是零个和一个出现.
  • r?等价于r|空集
  • ?与+与*有相同的运算集
• 字符类:[]
  
  • 一个正则表达式 a1 | a2 |...|an可以缩写为[a1a2...an]
  • 如果a1,a2,a2还具有逻辑关系,可以缩写为[a1-an]
    
    • 例如[1-9],[a-z]

3.3.6 3.3练习

• 第三题
  \/\*([^*"]*|".*"|\*+[^/])*\*\/

• 第四题
  先解决比较简单的{0,1,2}
  
  SB解法
  0?1?2?|0?2?1?|1?0?2?|1?2?0?|2?0?1?|2?1?0?|
  正确解法
    want -> 0|A?0?1(A0?1|01)*A?0?|A0?
    A -> 0?2(02)*
  证明如下面的图

  
  step3
  
  

• 5-7太难
  第八题:
  b*(a+b?)*
  第九题:
  b* | b*a+ | b*a+ba*

  Lex的扩展方法:

  

  如何引用这些被使用的符号

  

  3.4 词法单元的识别

• 我们学习如何根据各个需要识别的词法单元的模式来构造一段代码.

  • 识别检查输入的串,并找到匹配的词素.

3.4.1 状态转换图

介绍

• 词法分析器的中间步骤,将模式转换为状态转换图
• 本节用人工方式,将正则表示的模式转换为状态图
  
  • 3.6节介绍一种使用自动化方法来进行
• 状态转换图有一组被称为状态的结点和圆圈.

例子

3.4.2 保留字和标识符的识别

我们可以用两种方法处理像标识符的保留字.

• 初始化时将保留字填入符号表

• 为每个关键字建立单独的状态转换图

  

3.4.3 完成我们的例子

3.4.4 基于状态转换图的词法分析器的体系结构

有几种方法根据一组状态图构造出词法分析器.

例子

根据这个状态图,写出getRelop()函数

• 函数fail()具体操作依赖于全局恢复策略

  • 将forward指针重置为lexemeBegin的值
  • 使用另一个状态图从尚未处理的输入部分的真实位置开始识别.
  • 将state改为另一状态图的初始状态,将寻找别的词法单元
  • 当所有状态图都已经试过,fail()启动一个错误纠正步骤.

• 状态8,带有*,输入指针会回退,c放回输入流

  • 由retract()完成

• 状态图的执行

  • 顺序
  • 并行
    
    • 取最长的
  • 合并(麻烦)

3.4.5 3.4的练习

3.5 词法分析器生成工具 Lex

介绍一个名为Lex的工具,在最近的实现中也称为Flex.

• 支持使用正则表达式来描述词法单元的模式,给出一个词法分析器的规约
• 输入表示方法叫做Lex语言,工具本身是Lex编译器.
• 核心部分: 根据模式,生成转换图,生成相应代码,存放到lex.yy.c中

3.5.1 Lex的使用

• a.out 通常是语法分析器调用的子例程
• 子例程通常返回一个整数值,代表词法单元的编码
• 词法单元的属性值,保存在全局变量yylval中
  
  • 这个变量由语法分析器,词法分析器共享.

3.5.2 Lex 程序的结构

• 声明部分包括变量和明示常量(manifest con-stant)和正则定义

  • 明示常量,表示一个常数的标识符

• Lex的转换规则有如下形式
  模式 {动作}

  • 每个模式是一个正则表达式,可以使用声明部分的正则定义.
  • 动作部分是代码片段,一般是C语言

• Lex第三个部分包含各个动作要的辅助函数.

  • 还有一种方法将这些代码单独编译,一起装载

lex词法分析器和语法分析器的协同

• 当词法分析器被语法分析器调用时,词法分析从余下输入逐个读取字符.
  
  • 直到发现最长的与某个模式Pi匹配的前缀.
• 然后词法分析器执行动作Ai.
  
  • 通常Ai会返回语法分析器
  • 如果不返回控制,继续寻找其他词素,直到某个动作返回
• 词法分析器只返回一个值,即词法单元名
  
  • 在需要时,通过yylval传递词素附加信息

例子

• %{ %}
  
  

• 处理名为ID的词法单元的时候

  
  
  

3.5.3 Lex中的冲突解决

• 总是选择最长的前缀
• 如果最长的前缀与多个模式匹配,选择声明靠前的那个.

3.5.4 向前看运算符

某些时候,我们希望仅仅词素后面跟随特定字符,才能和模式匹配.

• 这种情况,我们使用/之后跟随表示一个附加的模式.
• 附加部分能匹配,但最后不属于词素

3.6 有穷自动机

揭示Lex如何将输入程序转换为词法分析器,核心在于有穷自动机

这些自动机本质和转换状态图类似,但也有以下不同

• 有穷自动机是识别器(recognizer).
  
  • 只能对每个输入串简单的回答 是,否.
• 有穷自动机分为两类
  
  • 不确定的有穷自动机(NFA):对其边上的标号没有任何限制,一个符号可以标记离开同一个状态的多条边.
  • 确定的有穷自动机(DFA):对于每个符号,有且一条离开该状态的边.

确定和不确定的能识别的语言的集合是相同的,恰好也是正则表达式能识别的集合,这个集合的语言叫做正则语言

3.6.1 不确定的有穷自动机

一个NFA由以下部分组成

• 一个有穷状态集合S
• 一个输入符号集合Σ,即输入字母表.
  
  • 假设空串不在这个集合.
• 一个转换函数,他为每个状态给出了相应的后继状态.
• S中的s0被称为开始状态
• S的一个子集F被称为接受状态

跟转换图有以下区别

• 同一个符号可以标记同一状态到达多个目标状态的多条边.
• 一个边的标号不仅可以是输入字母表的字符,也可是空串

例子

(a|b)*abb的NFA转换图

3.6.2 转换表

3.6.3 自动机输入字符串的接受

一个NFA**接受输入字符串x,当且仅当对应的转换图中存在一条开始状态到某个接受状态的路径,使得路径中各条变上的标号组成字符串x.

• 注意:路径的ε被忽略

• 我们可以用L(A)表示自动机A接受的语言

3.6.4 确定的有穷自动机

• 在构造词法分析器时,我们真正实现和模拟的是DFA.
• ?幸运的是,每个正则表达式和每个DFA都可以转变为接受相同语言的DFA.

如何用DFA进行串的识别(十分简单)

3.7 从正则表达式到自动机

• 首先介绍如何把NFA转换为DFA.

  • 利用子集构造法的技术给出一个直接模拟NFA的算法
    
    • 这个算法可用于那些将NFA转化为DFA比直接模拟NFA更加耗时的(非词法分析)情形

• 接着,我们介绍正则表达式转为NFA

  • 在必要时刻,根据这个NFA构造DFA

• 最后讨论不同正则表达式实现技术的时间-空间权衡,并说明如何选择正确的方法.

3.7.1 从NFA到DFA的自动转换

子集构造法的基本思想:是让构造得到的DFA的每个状态对应于NFA的一个状态集合.

• DFA在读入输入a1a2...an之后到达的状态对应于相应NFA从开始状态出发,沿着以a1a2...an为标号走到的路径能够到达状态的集合.

• DFA状态数可能是NFA状态数的指数,此时试图实现这个DNA有点困难.

• 然而,基于自动机的词法分析方法的处理能力部分基于这个事实:

  • 对于一个真实的语言,它的NFA和DFA的状态数量大致相同,状态数量呈指数尚未在实践中出现

子集构造算法

输入: 一个NFA N
输出: 一个接受同样语言的 DFA D

方法: 我们的算法为D构造一个转换表Dtran.

• D的每个状态是一个NFA状态集合,我们将构造Dtran,使得D “并行的” 模拟N在遇到一个给定输入串可能执行的所有动作.

• 第一个问题:正确处理N的`转换.

• 给出一些基本操作 s表示N的单个状态,T表示一个状态集.

  

• 算法代码(有ACM功底很容易懂):

  

• D的开始状态是ε-closure(s0),D的接受状态是所有至少包含N的一个接受状态的状态集合,

• ε-closure(T)代码,一个简单的深搜而已

  

例子

• A和C可以合并,将在后面介绍DFA的最小化问题.

3.7.2 NFA的模拟

许多的文本编辑器使用的策略是根据一个正则表达式构造出相应的NFA,然后使用类似于on the fly(边构造边)的子集构造法来模拟这个NFA的执行.

算法:模拟一个NFA的执行

也类似广搜,一步一步把所有情况跑一遍.

3.7.3 NFA模拟的效率

更详细的介绍这个算法

需要以下数据结构

• 两个堆栈,其中每个堆栈都存放了一个NFA状态集合.

  • 堆栈oldStates存放 “当前状态集合”
  • 堆栈newStates存放 “下一个状态集合”

• 一个以NFA状态为下标的布尔数组 alreadyOn,指示那个状态已经在newStates.

• 一个二维数组 move[s,a],保存了这个NFA的转换表,是一个邻接表(因为转换表单元格有多个元素).

• 既然书说他是O(k(m+n))复杂度…那就是吧

3.7.4 从正则表达式构造NFA

现在给出一个算法,它可以将任何正则表达式转为接受相同语言的NFA

• 这个算法是语法制导的,沿着正则表达式的语法分析树自底向上递归处理.
• 对于每个子表达式,该算法构造一个只有一个

算法 3.23 将正则表达式 转换为一个NFA的McMaughton-Yamada-Thompson算法

• 基本规则

  • 

• r=s|t

  

• r=st

  

• r=s*

  

• 几个有趣的性质

  • N(r)的状态数最多是 r中出现的运算符和运算分量的总数的2倍.
  • N(r)有且只有一个开始状态,接收状态没有出边,开始状态没有入边.
  • 除接受状态,都最多有一条带字符的出边,最多有两条空边

例子

3.7.5 字符串处理算法的效率

• 子集构造法 : O(|r|^2 * DFA状态数) DFA状态数一般是|r|

• 模拟算法: O(|r|*|x|)

3.8 词法分析器生成工具的设计

• 应用3.7中介绍的技术,讨论Lex这样生成工具的体系
• 将讨论基于NFA和DFA的方法,后者实质上就是Lex的实现方法

3.8.1 生成的词法分析器的结构

3.8.2 基于NFA的模式匹配

• 沿着状态集回头寻找直到有一个完成状态

3.8.3 词法分析器使用的DFA

3.8.4 实现向前看运算符/

3.9 基于DFA 的模式匹配器的优化

本节给出三个算法,用于实现和优化根据正则表达式构建的模式匹配器

• 第一个算法可以用于Lex编译器
  
  • 可以不用经过构造中间NFA就能构建DFA,
  • 得到的DFA状态数也比经过中间NFA得到的DFA状态数少
• 第二个算法,可以将任何DFA未来具有相同行为的状态合并.
  
  • 算法复杂度O(nlogn)
• 第三个算法,可以生成比标准二维表更加紧凑的转换表方式.

3.9.1 NFA的重要状态

• 如果一个NFA状态有一个标号非ε的离开转换,则称这个状态是重要状态(important state)

  • ε-closure(move(T,a)),它只使用了集合T中的重要状态.
  • 只要当集合s是重要状态时,move(s,a)才可能是非空的.

• 在子集构造法中,两个NFA状态可以被认为是一致的的条件是:

  • 1.具有相同的重要状态
  • 2.要么包含接受状态,要么都不包含接受状态.
  • 一致的意思是把它们当做同一个集合来处理.

正则转换的NFA

• 如果NFA由正则表达式生成,还有更多关于重要状态的性质

  • 重要状态只包括在基础规则部分为正则表达式中某个特定符号位置引入的初始状态.
  • 也就是说,每个重要状态对应于正则表达式某个运算分量.
  • 在正则表达式后面加一个#变为(r)#,使得原本的接受状态变为重要状态,使得在构造过程中,不要考虑接受状态.
    
    • (r)#又叫扩展的正则变道时

• 使用抽象语法树表示扩展的正则表达式.

  • 叶子节点代表运算分量
  • 内部节点表示运算符号

• 整数叫做叶子节点的位置,也表示他对应符号的位置
  
  • 一个符号可以有两个位置:比如a有1和3

3.9.2 根据抽象语法树计算的到的函数

• 要做一个正则表达式直接构造出DFA,我们首先要构造它的抽象语法树
• 然后计算如下四个函数:nullable,firstpos,lastpos和followpos.
  
  • 都是在(r)#下进行的.
  • nullable(n):对于一个节点n当且仅当此节点代表的子表达式中包含空串ε返回真
    
    • 子表达式可以生成空串或者自己就是空串,即使能生成一些其他串
  • firstpos(n):以节点n为根的子树中的位置集合.
    
    • 这些位置对应于以n为根的子表达式的语言中某个串的第一个符号.
  • lastpos(n):以节点n为根的子树中的位置集合.
    
    • 这些位置对应于以n为根的子表达式的语言中某个串的最后一个符号.
  • followpos(p):定义了一个和位置p相关的,某些位置的集合.
    
    • 一个位置q在 followpos(p)中当且仅当存在L((r)#)中的某个串x=a1a2...an,使得我们在解释为什么x属于L((r)#)时,可以将x中某个ai可以和位置p匹配,且将位置ai+1和位置q匹配

3.9.3 计算nullable,firstpos和lastpos

• 直接树形递归就行

3.9.4 计算followpos

只有两种情况,正则表达式某个位置会跟在另一个位置之后

• 如果n是一个cat节点,且左右节点是c1,c2.
  
  • 那么对于lastpos(c1)中的每个位置i,firstpos(c2)中的所有位置都在followpos(i)中.
  • 如果 n 是 star节点,并且i是 lastpos(n)中的一个位置,那么firstpos(n)中的所有位置都在followpos(i)中.

例子

3.9.5 根据正则表达式构建DFA

算法3.3.6 从一个正则表达式r构造DNF

• 根据扩展表达式(r)#构造出一颗抽象语法树T
• 计算T的函数nullable,firstpos,lastpos,followpos
• 使用下列程序,构造出D的状态集Dstates和D的转换函数Dtran

3.9.6 最小化一个DFA的状态数

(数电中有提及)

任何正则语言都一个唯一的(不计同构)状态数目最少的DFA.,从任意一个接受相同语言的DFA出发,通过分组合并等价的状态,我们总是构建这个状态数最少的DFA.

算法

• 该算法首先创建输入DFA的状态的集合的划分.

• 输入串如何区分各个状态:

  • 如果分别从状态s和t出发,沿着标号为x的路径到达的两个状态中只有一个是接受状态,我们说串x区分状态s和状态t的串
  • 如果存在一个串能区分s和t,那么他们是可区分的.

• DFA状态最小化的工作原理是将一个DFA的状态集合分划成多个组,每个组中的各个状态之间相互不可区分.

算法3.39

之后就类似于缩点的算法.

例子版本:

3.9.8 DFA模拟中的时间和空间权衡

• 转换链表压缩

  

• 一种方式,即有数组的便携,又有链表压缩的默认状态.

  

  

  • 如何保存base值比较好