Python数据分析练习01—二手车折旧/价格分析

搜索一些能用来进行数据分析探索的数据
利用Python对数据进行处理、制图、分析等来练习

1. 背景

通过二手车交易数据了解二手车行情，从中分析影响二手车价格的因素。

2. 说明

本文数据来源：https://www.kesci.com/home/project/5d2d821a688d36002c5f2d3b/dataset
python版本：3.5.2

3. 载入相关库

载入处理文件、表格、数据的库，以及可视化图形的库。

import pandas as pd
import matplotlib.pyplot as plt
import matplotlib.ticker as mtick
import os
import numpy as np
import collections
import seaborn as sns
import statsmodels.api as sm

4. 数据预处理

数据集是csv，因编码的问题另存为excel。

# 数据载入

data = pd.read_excel('second_cars_info.xlsx',encoding="ISO-8859-1")

# 数据字段处理
data['New_price'] = data['New_price'].str.extract('(\d+\.?\d+)',expand=True)#保留New_price字段的数字
data['Km'] = data['Km'].str.extract('(\d+\.?\d+)',expand=True)#保留KM字段的数字
data['Boarding_time'].loc[data['Boarding_time'] == '未上牌' ] = None # 将Boarding_time中未上牌的数据置为None
data['Boarding_time'] = pd.to_datetime(data['Boarding_time']) # 将Boarding_time转为时间
data['Boarding_time'] = data['Boarding_time'].apply(lambda x: x.year) # Boarding_time保留年份

# 字段数据类型更改
data['New_price'] = data['New_price'].astype('float')
data['Sec_price'] = data['Sec_price'].astype('float')
data['Km'] = data['Km'].astype('float')

# 对排放标准字段进行处理
discharge = data['Discharge'].str.split(',',expand=True)
discharge[1].loc[discharge[2].isnull() == False] = discharge[2]
discharge[0].loc[discharge[1].isnull() == False] = discharge[1]
discharge[0].loc[discharge[0] == 'OBD'] = '欧4'
data['Discharge'] = discharge[0]

# 将款式年份特征提取
type = data['Name'].str.split('款',expand=True)
type = type[0].str.extract(r'([-\s]\d{4})',expand=True)
data['type_year'] = type
data['type_year'] = data['type_year'].astype('float')

# 特征添加折旧率与车龄
data['zhejiu'] = data.apply(lambda x: x['Sec_price'] / x['New_price'], axis=1)
data['Year'] = data.apply(lambda x: 2018 - x['Boarding_time'], axis=1)

通过data.head()查看处理结果

通过data.info()查看非空值样本数及它们的数据类型

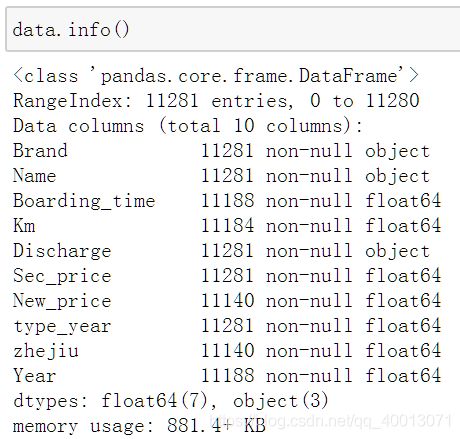
通过data.describe()查看样本的数据特征概要

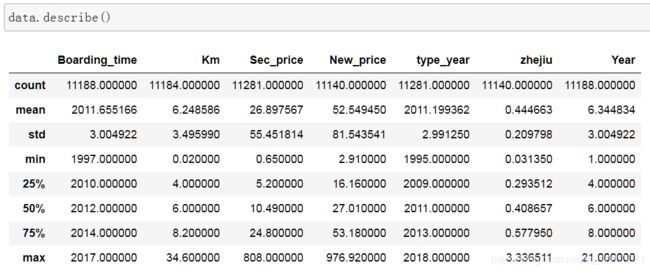
在这一批二手车销售记录中，上牌时间和车的款式时间平均值为2011年。平均成交价格是车原本价格的二分之一，即价格折旧大概在五成左右。平均里程数为6千米，并且75％的二手车里程不超过8.2千米。

5. 数据探索分析

5.1 销量分析

鉴于二手车品牌众多，在该市场中也可能会有垄断的现象出现。将销量排名前十的品牌统计出来单独计算，剩余的品牌合集为“其他”。

word_counts = collections.Counter(data['Brand']) # 对分词做词频统计
word_counts_top10 = word_counts.most_common(10) # 获取前10最高频的词
plt.rcParams['figure.figsize'] = (10, 7) # 设置figure_size尺寸
brand = []
brand_num = []
for i in range(0,10):
    brand.append(word_counts_top10[i][0])
    brand_num.append(word_counts_top10[i][1])
brand.append('其他')
brand_num.append(data.shape[0] - sum(brand_num))

plt.rcParams['font.sans-serif'] = ['Microsoft YaHei']
plt.pie(brand_num, labels=brand,autopct='%1.2f%%',startangle=90,radius = 1.5,textprops={'fontsize':11,'color':'black'})
plt.axis('equal')
plt.show()

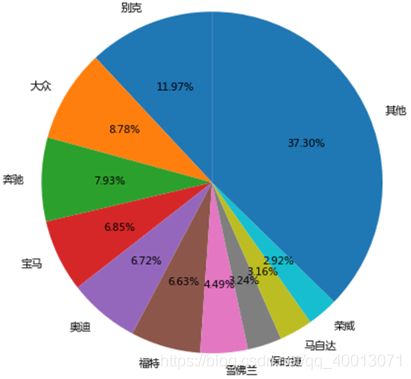
从统计图来看，销量前十的品牌占了总销量约63%。销量突出的品牌有别克、大众、奔驰、宝马等。

除了品牌以外，不同款式不同年份的销量也不同。以下以二手车的款式年份进行统计分析。

type_year = data['type_year'].value_counts()
type_year.plot(kind = 'pie')

在这一批二手车交易数据中，交易的二手车款式年份主要在2009至2015年，占据总销售的二手车中大约四分之三。卖出最多的二手车款式年份为2010、2011、2013年。

5.2 销售额分析

销售量大不一定代表销售额一定高，鉴于二手车行业有炒名牌车的现象，故分析各品牌的销售额情况。

weight_sum = pd.DataFrame(data.groupby('Brand',as_index=False)['Sec_price'].sum())
weight_sum = weight_sum.sort_values('Sec_price',ascending=False)

brand = weight_sum['Brand'].tolist()
secprice = weight_sum['Sec_price'].tolist()

brand = brand[:13]
brand.append('其他')
secprice1 = []
for i in range(0,13):
    secprice1.append(sum(secprice[:i+1]))
secprice1.append(sum(secprice))
secprice = secprice[:13]
secprice.append(secprice1[-1] - secprice1[-2])

pricepc = []
for i in range(0,14):
    pricepc.append(secprice1[i] / secprice1[-1] * 100)
    
plt.bar(brand,secprice, width=0.6, align='center', label=u"销售金额")
plt.xlabel(u"品牌")
plt.ylabel(u"销售金额（万）")
handles1, labels1 = plt.gca().get_legend_handles_labels()
plt.twinx()
plt.plot(brand, pricepc ,"r", marker='*', ms=10, label=u"累计百分比")
fmt = '%.1f%%'
yticks = mtick.FormatStrFormatter(fmt)
plt.gca().yaxis.set_major_formatter(yticks)
plt.ylabel(u"累计百分比")
handles2, labels2 = plt.gca().get_legend_handles_labels()
plt.legend(handles1+handles2, labels1+labels2, loc='upper left')

从统计图中可得，销售总金额排名11（总售额大于1亿）以上的占了接近总销售额的70%。其中奔驰的二手车销售总额占所有二手车的15.7%，是总销售额最高的品牌。其次是宾利、宝马、保时捷。同时这几款的销售量也较高，可见人们在购买二手车上，选择豪车的较多。

5.3 排放标准分析

由图，这一批次二手车排放标准为国4的最多，占比40.3%，其次是欧4（18.1%）、国5（14.5%）、欧5（11.2%）。根据前文展示的二手车款式年份分布，在2009年至2015年间的车生产时是符合国4标准。在2018年开始全面施行国5标准的汽车生产。

discharge = data['Discharge'].value_counts()
discharge.plot(kind = 'bar')

5.4 折旧分析

5.4.1 车龄分析

这一批交易的二手车数据中，成交最多的车的车龄为8年，即2010年附近上牌的车。其次为4年，为2014年上牌的车。从分布中来看，大致符合正态分布。

car_year = data['Year'].value_counts()
car_year.to_frame().sort_index().plot(kind = 'bar')

5.4.2 里程分析

将二手车里程数据分为6类，从里程为0开始每隔3万千米为一组。

kmBins = [0,3,6,9,12,15,1000000]
kmlabels = ['0_3','4_6','7_9','10_12','13_15','16+']
km = pd.cut(data['Km'], bins=kmBins, labels=kmlabels, include_lowest=True)
km.value_counts().to_frame().sort_index().plot(kind = 'bar')

从图可看出，大部分交易的二手车里程数在0到9万千米之间。卖出最多的二手车里程数为7到9万千米，其次为4到6万千米。说明大部分客户对于二手车里程数的需求在低于9万千米左右。

6. 具体关系分析

对折旧价格进行分析。

zjBins = [0,0.2,0.4,0.6,0.8,1]
zjlabels = ['20%-','20%-40%','40%-60%','60%-80%','80%+']
zhejiu = pd.cut(data['zhejiu'], bins=zjBins, labels=zjlabels, include_lowest=True)
zhejiu.value_counts().to_frame().sort_index().plot(kind = 'bar')

由图可知，成交的二手车折旧价格在原价的20％至80％之间。只有极少部分客户会购买折旧价格低于20％以及高于80％的二手车，因折旧价格与车内折旧因素有一定关联。故从大部分客户心理来看，选择的不会是过于旧或新的二手车。准新车相较新车来说价格低了一点，但大部分客户如若有足够的资金宁愿多出一点钱购买全新的车。

将排放标准数值化。以进行相关性分析。将折旧价格、排放标准、里程、车龄进行相关性分析，以热图形式输出。

data['Discharge_level'] = 1
discharge_list = ['欧1','国2','欧2','国3','欧3','国4','欧4','国5','欧5','京5','欧6']
for i in discharge_list:
    data['Discharge_level'].loc[data['Discharge'] == i] = discharge_list.index(i) + 1
data['Discharge_level'].loc[data['Discharge'] == '--'] = None

names = ['折旧价格程度','排放标准等级','里程','车龄']
zhejiu = data[['zhejiu','Discharge_level','Km','Year']]
correction = zhejiu.corr() 
fig = plt.figure() 
ax = fig.add_subplot(figsize=(20,20))
ax = sns.heatmap(correction,cmap=None, linewidths=0.05,vmax=1, vmin=-1 ,annot=True,annot_kws={'size':10,'weight':'bold'})
plt.xticks(np.arange(4)+0.5,names)
plt.yticks(np.arange(4)+0.5,names)
ax.set_title('折旧价格影响因素相关系数热图')
plt.show()

继续分析二手车价格占原价百分比与各折旧因素的趋势。

fig, ax = plt.subplots(2,2)
data.plot(kind="scatter",x = 'Year',y = 'zhejiu',alpha=0.4,ax = ax[0,0])
data.plot(kind="scatter",x = 'Km',y = 'zhejiu',alpha=0.4,ax = ax[0,1])
data.plot(kind="scatter",x = 'Discharge_level',y = 'zhejiu',alpha=0.4,ax = ax[1,0])

可以看出车龄越高，价格占原价百分比越低，二手车价格越便宜。里程数越高，价格占原价百分比越低，二手车价格越便宜。排放标准满足越高，价格占原价百分比越高，二手车价格越靠近原价。

再对折旧价格与折旧因素进行回归分析。

regression = data[['zhejiu','Discharge_level','Km','Year']].loc[data['zhejiu'].isnull() == False]
regression = regression.loc[regression['Discharge_level'].isnull() == False]
regression = regression.loc[regression['Km'].isnull() == False]
regression = regression.loc[regression['Year'].isnull() == False]

y = regression['zhejiu'].tolist()
x1 = regression['Discharge_level'].tolist()
x2 = regression['Km'].tolist()
x3 = regression['Year'].tolist()
def reg_m(y, x):
    ones = np.ones(len(x[0]))
    X = sm.add_constant(np.column_stack((x[0], ones)))
    for ele in x[1:]:
        X = sm.add_constant(np.column_stack((ele, X)))
    results = sm.OLS(y, X).fit()
    return results
print(reg_m(y, [x1]).summary())
print(reg_m(y, [x2]).summary())
print(reg_m(y, [x3]).summary())

从回归结果来看，车龄的回归拟合效果最好，满足车龄越高，相较原价折旧价格越低。排放标准的$R^2$为0.399，里程的$R^2$为0.408。
以下以车龄的回归输出来具体展示分析：
9
看完$R^2$后看Prob(F-statistic)，其表示F检验统计量，小于$\alpha$则可拒绝原假设，认为显著。
然后看P>|t|，表示P值大于t绝对值概率，越小越好。

其余的诸如log-likelihood，表示对数似然值。
[0.025,0.975] 表示置信区间95%。

假设折旧因素之间没有影响。从拟合出的系数可以推出，排放标准提升一个等级，其他条件相似的情况下，相较原二手价，可提升相较原价8%的价格。里程数高1万千米，二手车降3%的价格。车龄提高1年，二手车降低6%的价格。
因排放标准的提升本身对车的生产有高要求，是硬性的条件无法更改。所以最后对二手车价格影响进行排序，为车龄、里程、排放标准。