区间最值查询-RMQ（ST算法）

在打各种ACM比赛时，经常都会出现与区间有关的题目，有的是直接要求求解区间问题，有的是需要嵌套进其它算法作为优化手段出现。

很常见的区间问题有区间查询,区间最值等。有的是需要单次查询，有的需要多次查询。

假如给定一个数组,要求多次查询给定区间的最大值,你会怎么做?

RMQ,全名即区间最大值/最小值查询(Range Minimum/Maximum Query)。

下面就是一个模板RMQ题。

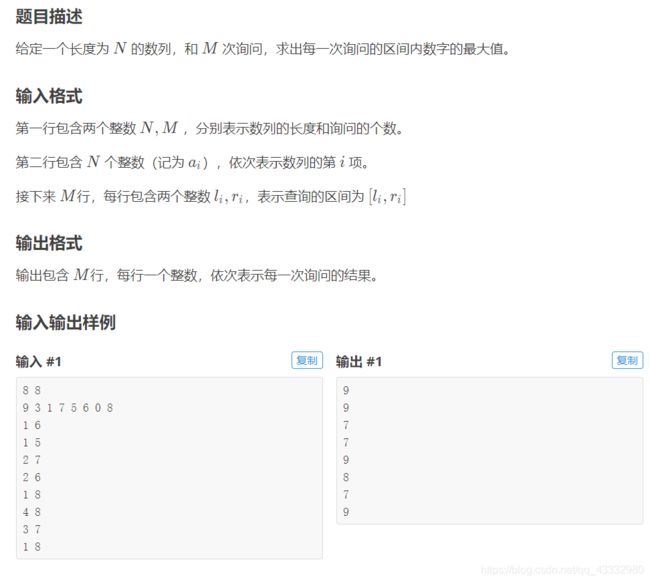
给定一个长度为 N 的数列，和 M 次询问，求出每一次询问的区间内数字的最大值。

洛谷(P3865 ST表)

最直接的方法是直接使用for循环遍历区间输出最大值。

单次查询可以这样，但面对M次查询，就意味着你需要遍历M个区间多次，最高复杂度可达O(N*M)，暴力解题需要慎重。

既然暴力不行，那么就使用有点技巧的方法。

区间最值可以使用线段树，但使用线段树最合适的地方是数组在动态变化的地方(后面博文介绍)，而对于静态数组的查询,则可以使用 ST表 解决。这里介绍用ST表解决静态区间查询问题，ST表预处理的复杂度为O(nlogn)，查询复杂度为O(1)。

ST算法

ST表的主体是一个二维数组 st[i][j] ，表示所需查询数组的从i到i+2^j-1间的最值。例如: st[2][3] 表示第2个数到第7个数的最大值。 ST算法的思想本质是动态规划。这里用S表示查询数组。

预处理

对于数组S,可以把其划分为两部分(A和B),那么数组S的最大值则是A的最大值或是B的最大值，取他们间最大的。

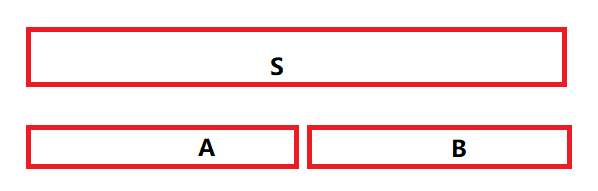
所以对于每一个st数组表示的区间，可以拆分成两部分，
状态转移方程为: st[ i ][ j ] = max{ st[ i ][ j-1 ] , st[ i+(1<<(j-1)) ][ j-1 ] } , (<<为位运算, 1<j )
划分的区间为 ( i, i+2^j ) -> ( i , i+2^j-1 ) + ( i+2^j-1 , i+2^j-1+ 2^j-1 )

当j=0时，2⁰=1，st[i][0] = S[i]。

void init()
{
	for(int i=1;i<=n;i++)
		st[i][0] = S[i];
	
	for(int j=1;(1<<j)<=S.length();j++)
		for(int i=1;i+(1<<(j-1))<=S.length();i++)
			st[i][j] = max(st[i][j-1],st[i+(1<<(j-1))][j-1];
}

查询

ST表建好后就要进行查询了，ST表里面包含的就是一个区间最值的信息，所以查询时则只需要通过给定区间(l,r)对ST表进行查询即可。

那么查询区间 (l,r) 该如何进行操作呢。由于st[i][j]是表示区间(i,i+2^j)，所以需要先了解(l,r)区间的长度， L = r-l+1，化为指数用k表示，k=log L 。

这时候只需要找到对应的st表的区间, 因为 L 一般来说不会刚好为 2的某个次方，或者说 由于log L 是向下取整的， 2^k一般会小于L，所以要确保取到正确的区间最值，可以在(l,r)的两头取， 取 (l,l+2^k) 与 (r-2^k+1,r) 区间的最值，这样虽然包含了重复部分，但不会影响结果。

所以 ans = max{ st[ l ][ k ], st[ r-(2<

int Query(int l,int r)
{
	int k = Log[r-l+1];
	ans = max(st[l][k],st[r-(1<<k)+1][k]
	return ans;
}

//初始化Log数组 计算log时直接查找
int Log[n+7];
void getLog()
{
	Log[1] = 0;
	for(int i=2;i<=n+1;i++)
		Log[i] = Log[i/2]+1;
}

题解

上面例题给出代码:

#include
#define MAX_N 100007    
#define MAX_M 25      // 2^25 > 100007
using namespace std;

int S[MAX_N],Log[MAX_N];
int st[MAX_N][MAX_M];

int n,m;

void init()
{
	for(int i=1;i<=n;i++)
		st[i][0] = S[i];
	
	for(int j=1;(1<<j)<=n;j++)
		for(int i=1;i+(1<<(j-1))<=n;i++)
			st[i][j] = max(st[i][j-1],st[i+(1<<(j-1))][j-1]);
}

void getLog()
{
	Log[1] = 0;
	for(int i=2;i<=n+1;i++)
		Log[i] = Log[i/2]+1;
}

int Query(int l,int r)
{
	int k = Log[r-l+1];
	return max(st[l][k],st[r-(1<<k)+1][k]);
}

//这里是快读
inline int read()
{
	int x=0,f=1;char ch=getchar();
	while (!isdigit(ch)){if (ch=='-') f=-1;ch=getchar();}
	while (isdigit(ch)){x=x*10+ch-48;ch=getchar();}
	return x*f;
}

int main()
{
	int l,r;
	n = read();
	m = read();
	for(int i=1;i<=n;i++)
		S[i] = read();
	getLog();
	init();
	for(int i=1;i<=m;i++){
		l = read();
		r = read();
		printf("%d\n",Query(l,r));
	}
	return 0;
}