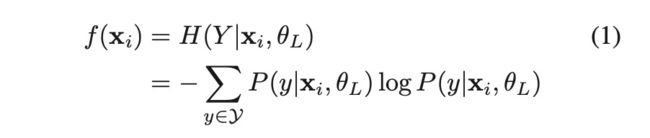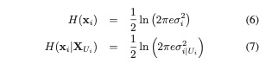Adaptive Active Learning for Image Classification 论文详解

如果需要看主动学习简介可以看上一篇博文：https://blog.csdn.net/GrinAndBearIt/article/details/107447026

        在计算机视觉领域，主动学习都是通过Uncertainty作为筛选样本的策略。如果未标注样本空间比较大，那么会存在挑选离群点的情况。论文中提出了information density和most uncertainty两种策略进行组合。然后筛选出critical instances给专家进行标注。

    针对仅通过不确定性容易筛选出对模型有伤害的离群点，可能会降低模型的性能。本篇论文提出一种新颖的自适应主动选择策略。包括（1）当前分类器的最不确定指标；（2）一种信息密度形式，能够衡量候选样本和未标注样本之间的相互信息；（3）两者自适应的组合

1. 不确定性度量（Uncertainty Measure）

根据论文的公式可以看出这就是一个计算信息熵的过程，首先基于已有的有标注数据训练分类器，通过训练好的分类器对未标注样本进行预测，对预测结果在各个类别的概率值计算信息熵，针对公式（1）中的P(y|xi,θL)，其中L代表已标注的样本集合，θL代表通过已标注样本进行训练分类器的参数，针对未标注样本xi分类为y的概率为P(y|xi,θL)

2. 信息密度形式（Information Density Meansure）

 

正如文中所说，提出信息密度形式的目的是为了解决不确定度量的缺点，这里使用上所有未标注的数据分布来挑选具有信息量的样本，过程如下：

（1）首先计算样本信息量（对整个未标注样本集的信息贡献程度）如式（3）所示。

    其中Hxi代表样本xi的信息，H(xi|XUi)表示未标注样本去除样本xi的信息量，XUi表示样本空间去除xi的样本集合，这里计算Hxi与上面不确定度量不一样，这里表示的是在样本空间（满足某种分布）中的信息量。

 

 

                            

那么接下来可能需要关注Hxi和H(xi|XUi)是怎么计算的了。

（2）这里假设公式（3）中的熵满足高斯过程，这里通过高斯核来逼近原本分布

 

    这里构建了未标注样本空间的相关矩阵

                              

（3）其中根据高斯核的公式计算算K(xi,xi)=σ2

                      

PxiXUi=P(ℵ(xi)|ℵ(Ui))也服从高斯分布，其方差可以表示为：

                   

 

(4) 根据高斯分布的熵计算得到

                              

 

（5）最后计算样本的信息量为

                                          

 

3. 组合框架

   计算完不确定性度量和信息密度形式后，文中作者应用了自适应的方式组合不确定性度量和信息密度形式

                            

4. 自适应组合（Adaptive Combination）

    从上面公式可以发现参数选择很重要，当β<0.5，density比uncertainty更重要；β>0.5，uncertainty比density更重要；β=1时，相当于只使用uncertainty。

     文中作者先选择一个不同的β值，一共b个，例如B=[0.1,0.2…..,1]根据不同的β值选取样本，通过两次筛选选择最优的样本     

                                         

整体流程如下:

                                                     

参考文章：

[1] https://www.cv-foundation.org/openaccess/content_cvpr_2013/papers/Li_Adaptive_Active_Learning_2013_CVPR_paper.pdf

[2] https://blog.csdn.net/Lucifer_zzq/article/details/102677814