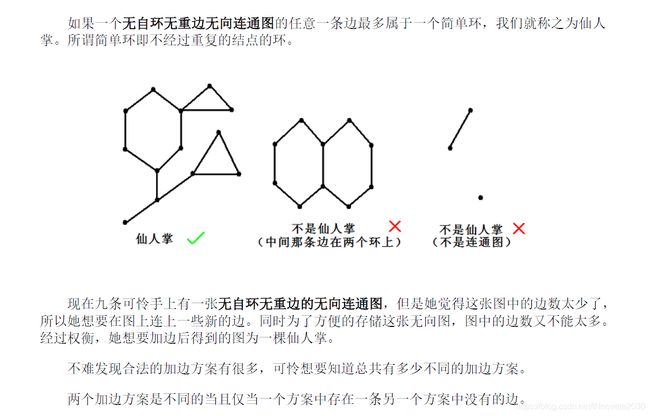
【ZJOI2017】仙人掌

【ZJOI2017】仙人掌

题目描述：

数据范围：

这道题很难写暴力啊QWQ。
先推荐一个博客，我就是看这个会的：https://www.cnblogs.com/wfj2048/p/6636028.html

首先我们先判断这个图是不是个仙人掌。显然，如果一个点到钦定根的路径数大于2那么就一定不是仙人掌。

在仙人掌上DP并不好做，于是我们考虑把仙人掌拆成许多棵树，在树上跑DP。

引入$F_{num}$ 代表对于一个节点有$num$个儿子，儿子之间两两相连的方案数。显然$F_i=F_{i-1}+(i-1)\ast F_{i-2}$。

我们把节点分为根和非根。对于根答案肯定是$f_u=(\Pi f_v)\ast F_{num}$。非根也很简单，对于自己来说父亲也是一个可以连的点，相当于儿子加一。

这样做为什么是对的？如果两个点（默认树上）不在同一条链上，连边，它们的贡献如何被记录？

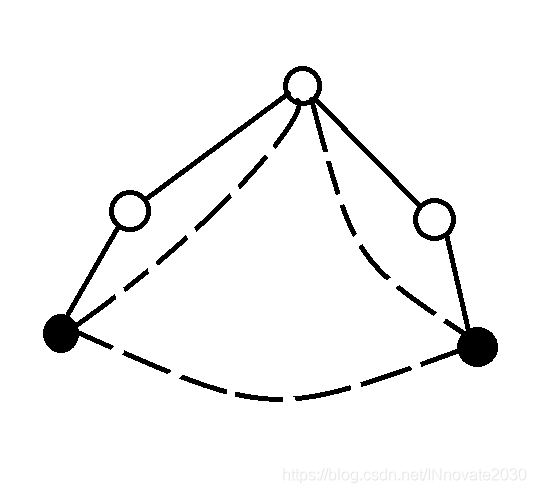
例如图中两个黑色的节点。
它们的连线与其它边组成合法方案，相当于左边路径覆盖和右边路径覆盖乘积。而这在转移时被统计进去，所以我们可以不用单独考虑这种横插边也能统计答案。

#include 
#include 
#include 
using namespace std;

const int P = 998244353;
const int N = 500010,M = 1000010;

template < class T >
inline void read(T &x)
{
	char ch = getchar(); x = 0; int fg = 1;
	for(;ch < '0' || ch > '9';)fg = ch == '-' ? -1 : 1, ch = getchar();
	for(;ch >= '0' && ch <= '9';) x = x * 10 + (ch ^ '0'), ch = getchar(); x *= fg;
}

struct node{ int d,id; } a[N];
struct Edge{ int to,nxt; } g[M << 1];
int last[N],cnt = 1,tag[N],fa[N],dep[N],dfn[N],T,n,m,tot,vis[N];
long long f[N],F[N] = { 1,1 },ans = 1;

int cmp(node a,node b) { return a.d < b.d; }

void add(int u,int v) { g[++cnt] = (Edge){ v,last[u] }, last[u] = cnt; }

void dfs(int x)
{
	dfn[x] = ++tot, dep[x] = dep[fa[x]] + 1;
	for(int i = last[x];i;i = g[i].nxt)
		if(g[i].to != fa[x] && !dep[g[i].to]) fa[g[i].to] = x, dfs(g[i].to);
}

void dfs(int x,int fg)
{
	vis[x] = f[x] = 1; int num = 0;
	for(int i = last[x];i;i = g[i].nxt)
		if(g[i].to != fa[x] && tag[g[i].to] == 1 && !vis[g[i].to])
			++num, dfs(g[i].to,0), f[x] = 1ll * f[x] * f[g[i].to] % P;
	if(fg) f[x] = 1ll * f[x] * F[num] % P; else f[x] = 1ll * f[x] * F[num + 1] % P;
}

int main()
{
	freopen("cactus.in","r",stdin);
	freopen("cactus.out","w",stdout);
	
	for(int i = 2;i < N; ++ i) 
		F[i] = 1ll * (F[i - 1] + 1ll * (i - 1) * F[i - 2] % P) % P;
	for(read(T);T--;ans = 1,cnt = 1,tot = 0)
	{
		read(n), read(m); int fg = 1;
		for(int i = 1;i <= n; ++ i)
			vis[i] = tag[i] = fa[i] = dfn[i] = dep[i] = last[i] = 0; 
		for(int i = 1,u,v;i <= m; ++ i)
			read(u), read(v), add(u,v), add(v,u); dfs(1);
		for(int i = 2,x,y;i < cnt;i += 2)
		{
			x = g[i].to, y = g[i ^ 1].to;
			if(dfn[x] < dfn[y]) swap(x,y);
			for(;x != y;) { if(tag[x] == 2) { printf("0\n"); fg = 0; break; }; ++ tag[x]; x = fa[x]; }
			if(!fg) break;
		} if(!fg) continue;
		for(int i = 1;i <= n; ++ i) a[i] = (node){ dep[i],i };
		sort(a + 1,a + 1 + n,cmp);
		for(int i = 1;i <= n; ++ i)
			if(!vis[a[i].id]) dfs(a[i].id,1), ans = 1ll * ans * f[a[i].id] % P;
		printf("%lld\n",ans); 
	}
	
	fclose(stdin); fclose(stdout);
	return 0;
}