后端开发 面试题整理

面向对象（C/C++)

引用和指针的区别

• 都是地址的概念。
• 指针指向一块内存，它存储的是所指内存的地址，而引用是某块内存的别名。
• 引用不可以为空，但指针可以为空。
• 引用只能在定义时被初始化一次，之后不可变。
• 指针需要解引用。

堆、栈

• 栈：由操作系统自动分配释放，存放函数的参数值、局部变量等。删除与加入均在栈顶操作，是一种线性表。栈使用的是一级缓存，通常被调用时处于存储空间中，调用完毕立即释放，一种先进后出的数据结构。
• 堆：堆是指程序运行时申请的动态内存，而不是在程序编译时，分配方式类似于链表，栈只是指一种使用堆的方法。堆是放在二级缓存中，生命周期由虚拟机的垃圾回收算法决定，堆可以被看成是一棵树。

STL_Map

底层是用红黑树实现的，查找的平均复杂度是log(n)，map的key是有序的，因为是用红黑树实现的，所以key是中序遍历出来的。
hash_map是用hash实现的map，key是无序的，hash_map查询是O(1)的。
hashtable就是手写的hash表。

虚函数

用virtual关键字申明的函数叫做虚函数，是类的成员函数，虚函数是用于实现多态的机制，核心理念就是通过基类访问派生类定义的函数，只能借助于指针或者引用来达到多态的效果。
存在虚函数的类都有一个一维的虚函数表叫做虚表。当类中声明虚函数时，编译器会在类中生成一个虚函数表，其中存放着该类所有的虚函数对应的函数指针。

C++的构造函数可以是虚函数吗？

构造函数不能为虚函数，而析构函数常常是虚函数。

1. 从存储空间角度：
   虚函数对应一个虚表，vtable是存储在对象的内存空间的。如果构造函数是虚的，就需要通过 vtable来调用，但是对象没有实例化的时候就没有内存空间，也就不存在vtable，所以构造函数不能是虚函数。
2. 构造函数不允许是虚函数，因为创建一个对象时需要明确对象的类型。但析构往往通过基类的指针来销毁对象，如果析构函数不是虚函数，就不能正确识别对象类型从而不能正确调用析构函数。

解决哈希冲突的方法

1. 开放定址法
   基本思想是：当关键字key的哈希地址p出现冲突时，以P为基础，产生另一个哈希地址P1，如果P1仍然冲突，再以P为基础，产生另一个哈希地址P2，直到找出一个不冲突的哈希地址Pi ，将相应元素存入其中。
2. 链地址法
   将所有哈希地址为 i 的元素构成一个同义词链的单链表，并将单链表的头指针存在哈希表的第i个单元中，因而查找、插入和删除主要在同义词链中进行。链地址法适用于经常进行插入和删除的情况。
3. 再哈希法
   当hash地址发生冲突时，再次计算hash值，直到不冲突为止，这种方法不易产生聚集，但增加了计算时间。

C++的struct和类的区别

C++结构体的继承默认是public，而c++类的继承默认是private。
C++结构体内部成员变量及成员函数默认的访问级别是public，而c++类的内部成员变量及成员函数的默认访问级别是private。

面向对象的三大特性

1. 封装
   封装就是隐藏对象的属性和实现细节，仅对外公开接口，控制在程序中属性的读和修改的访问级别。封装的目的是增强安全性和简化编程，使用者不必了解具体的实现细节，而只是要通过外部接口，以特定的访问权限来使用类的成员。
2. 继承
   继承就是子类继承父类的特征和行为，使得子类对象具有父类的实例域和方法，或子类从父类继承方法，使得子类具有父类相同的行为。
3. 多态
   同一个行为具有多个不同表现形式或形态的能力，是指一个类实例的相同方法在不同情形有不同表现形式。

多态的实现

多态分为静态多态与动态多态。

• 静态多态就是重载，在编译时就可以确定函数地址。
• 动态多态就是通过继承重写基类的虚函数实现的多态，在运行时确定。运行时在虚函数表中寻找调用函数的地址。
• 在基类的函数前加上virtual关键字，在派生类中重写该函数，运行时将会根据对象的实际类型来调用相应的函数，如果对象类型是派生类，就调用派生类的函数，如果对象类型是基类，就调用基类的函数。
• 存在虚函数的类都有一个一维的虚函数表叫做虚表，类的对象有一个指向虚表开始的虚指针。虚表是和类对应的，虚表指针是和对象对应的。

区分重载、重写和隐藏。

• 重载：同一类中，函数名相同，但参数列表不同。
• 重写：父子类中，函数名相同，参数列表相同，且有virtual修饰。
• 隐藏：父子类中，函数名相同，参数列表相同，但没有virtual修饰。

五大基本原则

1. 单一职责原则：一个类只完成一个功能。
2. 开放封闭原则：对象或实体应该对扩展开放，对修改封闭。
3. 里氏替换原则：所有引用基类的地方必须能透明地使用其子类的对象。
4. 依赖倒置原则：抽象不应该依赖于细节，细节应该依赖于抽象。
5. 接口隔离原则：客户端不应该依赖它不需要的接口，类间的依赖关系应该建立在最小的接口上

Struct 和 Union有下列区别：

• 在存储多个成员信息时，编译器会自动给struct第个成员分配存储空间，struct 可以存储多个成员信息，而Union每个成员会用同一个存储空间，只能存储最后一个成员的信息。
• 都是由多个不同的数据类型成员组成，但在任何同一时刻，Union只存放了一个被先选中的成员，而结构体的所有成员都存在。
• 对于Union的不同成员赋值，将会对其他成员重写，原来成员的值就不存在了，而对于struct 的不同成员赋值 是互不影响的。

define和const区别：

• define是宏定义，程序在预处理阶段将用define定义的内容进行了替换。因此程序运行时，常量表中并没有用define定义的常量，系统不为它分配内存，const定义的常量，在程序运行时在常量表中，系统为它分配内存。
• define定义的常量，预处理时只是直接进行了替换，所以编译时不能进行数据类型检验。const定义的常量，在编译时进行严格的类型检验，避免出错。
• define定义表达式时要注意“边缘效应”，例如如下定义：#define N 2+3 我们预想的N值是5，我们 int a = N/2，我们预想的a的值是2，可实际上a的值是3。原因在于在预处理阶段，编译器将 a = N/2处理成了 a = 2+3/2。

static

1. 静态变量是堆分配的，而动态变量是在栈上分配的。静态变量只会初始化一次，在变量定义时就分定存储单元并保持不变，直至整个程序结束
2. 函数体内static变量的作用范围为该函数体，在类中的static成员属于全局变量，静态方法只能访问类的static成员变量。

const

1. const 常量：定义时就初始化，以后不能更改
2. const修饰形参，表明它是一个输入参数，在函数内部不能改变其值
3. const修饰类成员函数：该函数对成员变量只能进行只读操作

New/delete. Malloc/free.

• new是先自动判断大小再去申请内存，再调用构造函数，返回一个指向该对象的指针。失败抛出异常。
• delete是调用析构函数，然后释放内存。
• malloc申请你给的内存大小，返回这块内存的指针（void*）。失败返回NULL。
• free是直接释放内存和指针。
• malloc有内存扩容，new没有。

vector和list的区别

• vector和数组类似，拥有一段连续的内存空间，但是vector是动态申请内存的，并且起始地址不变。能高效的进行随机存取，时间复杂度为o(1)，但进行插入和删除操作时，会造成内存块的拷贝，复杂度为o(n)。
• list是由双向链表实现的，因此内存空间是不连续的。只能通过指针访问数据，所以list的随机存取效率非常低，时间复杂度为o(n)，但由于链表的特点，能高效地进行插入和删除。
• 总之，如果需要高效的随机存取，而不在乎插入和删除的效率，使用vector；
  如果需要大量的插入和删除，而不关心随机存取，则应使用list。

常量指针和指针常量

int const* p 和 const int* p 是常量指针，也就是说这个指针指向的值不能变，但是这个指针的地址可以变。
int *const p 是指针常量，指针的地址不能变，但是指向的值可以变，所以要初始化。

内存泄漏

程序申请的内存空间，在使用完毕后未释放，一直占据内存单元。
解决方法：良好的代码习惯，在涉及内存的程序段检测内存泄漏。重载new和delete，主要思路是将分配的内存以链表的形式自行管理，使用完成之后从链表中删除，程序结束时可检查该链表，当中记录了内存泄露的文件，所在文件的行数以及泄露的大小。

智能指针

作用是监控内存的使用以及释放内存。首先指针只能是由两个类构成，分为引用计数类和指针类，其实智能指针的本质是类，但是看起来像指针。动态分配的资源，交给一个类对象去管理，当类对象声明周期结束时，自动调用析构函数释放资源，防止内存泄漏。

深拷贝和浅拷贝

• 浅拷贝只是增加了一个指针指向已存在的内存地址，深拷贝是在计算机中开辟一块新的内存地址用于存放复制的对象。
• 使用深拷贝的情况下，释放内存的时候不会因为出现浅拷贝时释放同一个内存的错误。

操作系统 -------------------------------------------------------------

进程和线程

• 一个任务就是一个进程，比如打开一个浏览器就是启动一个浏览器进程，有些进程不止同时做一件事，比如Word，它可以同时进行打字、拼写检查等。进程内的这些“子任务”就称为线程。
• 一个进程拥有多个线程，操作系统调度的基本单位是线程
• 线程 = 进程 – 共享资源
• 进程虽然不是调度的基本单位，但也能被调度。

多线程的优点和缺点

优点

1. 多线程技术使程序的响应速度更快 ,因为用户界面可以在进行其它工作的同时一直处于活动状态
2. 占用大量处理时间的任务使用多线程可以提高CPU利用率，即占用大量处理时间的任务可以定期将处理器时间让给其它任务
3. 多线程可以分别设置优先级以优化性能。

缺点

1. 如果有大量的线程,会影响性能,因为操作系统需要在它们之间切换.
2. 更多的线程需要更多的内存空间
3. 线程中止需要考虑对程序运行的影响.
4. 通常块模型数据是在多个线程间共享的,需要防止线程死锁情况的发生

进程间通信的方式

管道、消息队列、共享内存、套接字、信号量

• 管道：通常指无名管道，是半双工的通信（数据只能在一个方向上流动），具有固定的读写端。只能用于具有亲缘关系的进程之间的通信（也是父子进程或者兄弟进程之间），可以看成是一种特殊的文件，并不属于任何文件系统，只存在于内存中。
• 消息队列：消息队列是消息的链表，进程A可以向队列中写数据，队列中有数据了进程B就可以开始读数据了。消息队列克服了信号传递信息少、管道只能承载无格式字节流以及缓冲区大小受限等缺点。
• 共享内存：共享内存就是一块内存，在这块内存上的数据可以共同修改和读取，由于内存有随机访问的优势，所以共享内存就成为了进程间通信最快的方式。
• 套接字：套接字是网络编程的api，通过套接字可以不同的机器间的进程进行通信，常用于客户端进程和服务器进程的通信。
• 信号：操作系统通过信号来通知进程系统中发生了某种预先规定好的事件，它也是用户进程之间通信和同步的一种原始机制。一个键盘中断或者一个错误条件等都有可能产生一个信号。

线程间的同步方法

大体可分为两类：用户模式和内核模式

• 内核模式就是指利用系统内核对象的单一性来进行同步，使用时需要切换内核态与用户态。内核模式下的方法有：互斥量、信号量、事件。
  • 互斥量： 能够用于多个进程之间线程互斥问题，并且能完美的解决某进程意外终止所造成的“遗弃”问题
  • 信号量：它允许多个线程在同一时刻访问同一资源，但是需要限制在同一时刻访问此资源的最大线程数目
  • 事件：通过通知操作的方式来保持线程的同步，还可以方便实现对多个线程的优先级比较的操作
• 用户模式就是不需要切换到内核态，只在用户态完成操作。用户模式下的方法有：原子操作（例如一个单一的全局变量）、临界区
  • 临界区：在任意时刻只允许一个线程对共享资源进行访问，如果有多个线程试图访问公共资源，那么有一个线程进入后，其他试图访问公共资源的线程将被挂起，等到进入临界区的线程离开，临界区被释放后，其他线程才可以抢占。

死锁

• 多个进程在运行过程中因争夺资源而造成的一种僵局，当进程处于这种僵持状态时，若无外力作用，它们都将无法再向前推进。
• 产生的原因：竞争不可抢占性资源、竞争可消耗资源、进程推进顺序不当。
• 必要条件：互斥条件、请求和保持条件、不可抢占条件、循环等待条件。
  • 互斥条件：在一段时间内某资源仅为一进程所占用
  • 请求和保持条件：当进程因请求资源而阻塞时，对已获得的资源保持不放
  • 不可抢占条件：进程已获得的资源在未使用完之前，不能剥夺，只能在使用完时由自己释放
  • 循环等待条件：在发生死锁时，必然存在一个进程-资源的环形链。
• 处理的方法：预防死锁、避免死锁（银行家算法）、检测死锁、解除死锁。
  • 资源一次性分配：一次性分配所有资源，这样就不会再有请求了（破坏请求条件）
  • 只要有一个资源得不到分配，也不给这个进程分配其他的资源：（破坏请保持条件）
  • 可剥夺资源：即当某进程获得了部分资源，但得不到其它资源，则释放已占有的资源（破坏不可剥夺条件）
  • 资源有序分配法：系统给每类资源赋予一个编号，每一个进程按编号递增的顺序请求资源，释放则相反（破坏循环等待条件）

内存中的堆和栈的区别

申请方式和回收方式不同

• 栈上的空间是自动分配自动回收的，所以栈上的数据的生存周期只是在函数的运行过程中。
• 堆上的数据只要程序员不释放空间，就一直可以访问到，缺点是忘记释放会造成内存泄露。

申请后系统的响应

• 只要栈的剩余空间大于所申请空间，系统将为程序提供内存，否则将报异常提示栈溢出。
• 堆在申请的后，操作系统有一个记录空闲内存地址的链表，当系统收到程序的申请时，会遍历该链表，寻找第一个空间大于所申请空间的堆结点，然后将该结点从空闲结点链表中删除，并将该结点的空间分配给程序。

申请效率的比较

• 栈由系统自动分配，速度较快。但程序员是无法控制的。
• 堆由new分配的内存，一般速度比较慢，而且容易产生内存碎片，不过用起来最方便。

申请大小的限制

• 栈是向低地址扩展的数据结构，是一块连续的内存的区域。在 Windows下，栈的大小是编译时就确定的常数，如果申请的空间超过栈的剩余空间时，将提示overflow。因此，能从栈获得的空间较小。
• 堆是向高地址扩展的数据结构，是不连续的内存区域。这是由于系统是用链表来存储的空闲内存地址的，自然是不连续的，而链表的遍历方向是由低地址向高地址。堆的大小受限于计算机系统中有效的虚拟内存。

堆和栈中的存储内容

• 在函数调用时，第一个进栈的是主函数中函数调用后的下一条指令（函数调用语句的下一条可执行语句）的地址，然后是函数的各个参数，参数是由右往左入栈的，然后是函数中的局部变量，静态变量是不入栈的。
• 当本次函数调用结束后，局部变量先出栈，然后是参数，最后栈顶指针指向最开始存的地址，也就是主函数中的下一条指令，程序由该点继续运行。
• 一般是在堆的头部用一个字节存放堆的大小。堆中的具体内容有程序员安排。

存取效率的比较

• 在运行时刻赋值的是放在栈中。
• 在编译时就确定的是放在堆中。

虚拟内存

• 虚拟内存是计算机系统内存管理的一种技术。它使应用程序认为它拥有连续的可用的内存，而实际上，它通常是被分隔成多个物理内存碎片，还有部分暂时存储在外部磁盘存储器上，在需要时进行数据交换。使用这种技术的系统使得大型程序的编写变得更容易，对真正的物理内存的使用也更有效率。
• 用户程序开发方便、保护内核不受恶意或者无意的破坏、隔离各个用户进程

进程调度算法

• 先来先服务调度
• 短作业优先调度
• 优先级调度
• 高响应比优先调度
• 时间轮片调度
• 多级反馈队列调度

linux 系统中，一个被打开的文件可以被另一个进程删除吗？

可以。
Linux中每个文件都会有2个link计数器——i_count 和 i_nlink，删除操作只是将 i_nlink 置为 0 了，由于文件被进程引用的缘故，i_count 不为 0，所以系统没有真正删除这个文件。i_nlink 是文件删除的充分条件，而 i_count 才是文件删除的必要条件。

计算机网络----------------------------------------------------------

TCP协议和UDP协议的区别是什么

• TCP协议是通过三次握手建立连接的，会话结束之后也要结束连接。而UDP是无连接的。
• TCP协议保证数据按序发送，按序到达，提供超时重传来保证可靠性。但是UDP不保证按序到达，甚至不保证到达，只是努力交付。
• TCP协议所需资源多，TCP首部需要20个字节，UDP首部字段只需8个字节。
• TCP有流量控制和拥塞控制。UDP没有，网络拥堵会影响发送端的发送速率
• TCP是一对一的连接。而UDP则可以支持一对一，多对多，一对多的通信。
• TCP面向的是字节流的服务。UDP面向的是报文的服务

TCP报文中的序号和确认号的作用？

TCP可靠传输的关键部分。

• 序号是本报文段发送的数据组的第一个字节的序号。在TCP传送的流中，每一个字节一个序号。例如一个报文段的序号为300，此报文段数据部分共有100字节，则下一个报文段的序号为400。所以序号确保了TCP传输的有序性。
• 确认号，即ACK，指明下一个期待收到的字节序号，表明该序号之前的所有数据已经正确无误的收到。确认号只有当ACK标志为1时才有效。比如建立连接时，SYN报文的ACK标志位为0。

TCP三次握手

• 客户端向服务端发送连接请求，等待服务器确认
• 服务器收到请求报文后，如果同意连接，则发出确认报文。
• 客户进程收到确认后，再次向服务器发送确认信息，确认链接，TCP连接建立。
  

为什么A还要发送一次确认呢？可以二次握手吗？

防止已失效的连接请求报文段突然又传送到了B，因而产生错误。

如A发出连接请求，但因连接请求报文丢失而未收到确认，于是A再重传一次连接请求。后来收到了确认，建立了连接。数据传输完毕后，就释放了连接。但是第一个丢失的报文段只是在某些网络结点长时间滞留了，延误到连接释放后才到达B，此时B误认为A又发出一次新的连接请求，于是就向A发出确认报文段，同意建立连接。不采用三次握手，只要B发出确认，就建立新的连接了，此时A不理睬B的确认且不发送数据，则B一致等待A发送数据，浪费资源。

四次挥手

• 客户端进程发出连接释放报文，并且停止发送数据。
• 服务器收到连接释放报文，发出确认报文，服务端就进入了CLOSE-WAIT（关闭等待）状态。客户端收到服务器的确认请求后，客户端就进入FIN-WAIT-2（终止等待2）状态，等待服务器发送连接释放报文
• 服务器将最后的数据发送完毕后，就向客户端发送连接释放报文，由于在半关闭状态，服务器很可能又发送了一些数据，此时，服务器就进入了LAST-ACK（最后确认）状态，等待客户端的确认。
• 客户端收到服务器的连接释放报文后，必须发出确认，此时，客户端就进入了TIME-WAIT（时间等待）状态。服务器收到了客户端发出的确认，立即进入CLOSED状态，结束这次的TCP连接。服务器结束TCP连接的时间要比客户端早一些。
  

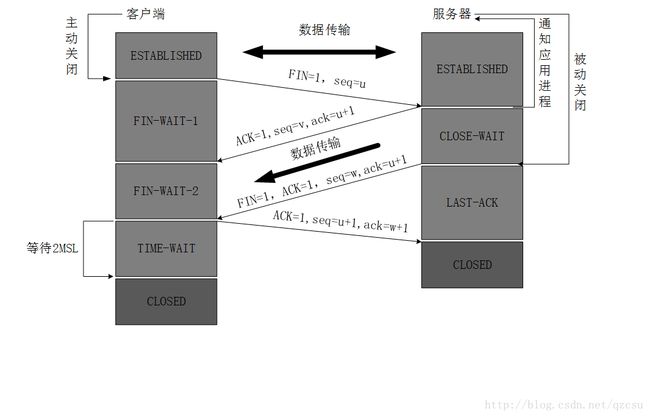
为什么连接的时候是三次握手，关闭的时候却是四次握手

当服务器端收到客户端的连接请求报文后，可以把SYN和ACK报文一起发送。其中ACK报文是用来应答的，SYN报文是用来同步的。但关闭连接时，当收到对方的FIN报文通知时，它仅仅表示对方没有数据发送给你了，但服务器端未必所有的数据都全部发送给对方了，可能还需要发送一些数据给对方之后，再发送FIN报文给对方来表示现在可以关闭连接了。

TCP协议是靠什么保证传输的可靠性的？

• 校验和：发送方在发送数据之前计算检验和，并进行校验和的填充。接收方，收到数据后，对数据以同样的方式进行计算，求出校验和，与发送方的进行比对
• 确认应答与序列号：TCP传输时将每个字节的数据都进行了编号，TCP传输的过程中，每次接收方收到数据后，都会对传输方进行确认应答，也就是发送ACK报文，报文中包含对应的确认序列号。
• 超时重传：发送方在发送完数据后等待一个时间，时间到达没有接收到ACK报文，那么对刚才发送的数据进行重新发送
• 连接管理：连接管理就是三次握手与四次挥手的过程
• 流量控制：发送端的发送速度太快，导致接收端的结束缓冲区填充满了，此时如果仍旧发送数据，那么接下来发送的数据都会丢包。TCP就会根据接收端对数据的处理能力，决定发送端的发送速度，这个机制就是流量控制。
• 拥塞控制：发送端在刚开始就发送大量的数据，那么就可能造成网络拥塞。所以TCP引入了慢启动的机制，在开始发送数据时，先发送少量的数据探路。

TCP拥塞控制

• 慢开始：在开始的时候发送的少，但是增长的速度是以指数的形式增长。
• 拥塞避免：当拥塞窗口达到一个阈值时，窗口大小不再呈指数上升，而是以线性上升，避免增长过快导致网络拥塞。
• 快重传：收到三个一样的回复报文的时候就重传该文件

TCP流量控制

滑动窗口：窗口大小指的是无需等待确认应答而可以继续发送数据的最大值，窗口越大, 则网络的吞吐率就越高。
接收窗口只有在前面所有的段都确认的情况下才会移动左边界，收到了一个返回确认的ACK之后窗口就往后移动继续发送在窗口里的数据。

五层协议的体系结构各层的主要功能

• 应用层：应用层是体系结构中的最高层，应用层协议定义的是应用进程间通信和交互的规则，应用层的任务是通过应用进程间的交互来完成特定网络应用，这里的进程就是指正在运行的程序。
• 运输层：负责为两个主机中进程之间的通信。主要使用以下两种协议：面向连接的传输控制协议TCP，和无连接的用户数据报协议UDP。
• 网络层：网络层为分组交换网上不同主机提供通信服务。网络层将运输层产生的报文段或用户数据报封装成分组和包进行传送。
• 数据链路层：两台主机间的数据传输，是一段一段在数据链路上传送的，需要专门的链路层协议，在两个相邻节点间的链路上传送帧，每一帧包括数据和必要的控制信息（如差错控制、流量控制）
  三个基本问题：封装成帧，透明传输，差错检测
• 物理层：透明地传送比特流。在物理层上所传数据的单位是比特。

一次完整的HTTP请求过程

1. 域名解析：得到了域名对应的IP地址
2. 浏览器发起HTTP请求
3. 然后到传输层，选择传输协议，TCP或者UDP，对HTTP请求进行封装，加入了端口号等信息
4. 然后到了网络层，通过IP协议将IP地址封装为IP数据报，此时会用到ARP协议，主机发送信息时将包含目标IP地址的ARP请求广播到网络上的所有主机，并接收返回消息，以此确定目标的物理地址，找到目的MAC地址
5. 接下来到了数据链路层，把网络层交下来的IP数据报添加首部和尾部，封装为MAC帧，现在根据目的mac开始建立TCP连接，三次握手，接收端在收到物理层上交的比特流后，根据首尾的标记，识别帧的开始和结束，将中间的数据部分上交给网络层，然后向上传递到应用层
6. 服务器响应请求并请求客户端要的资源，传回给客户端
7. 断开TCP连接，浏览器对页面进行渲染呈现给客户端。

数据结构--------------------------------------------------------------

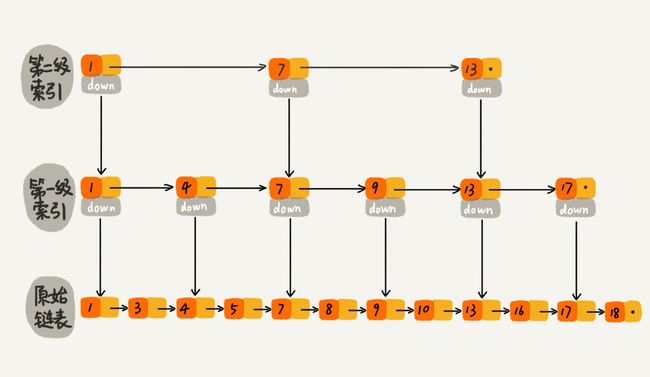
跳表

跳表是redis的一个核心组件，也被广泛地运用到了各种缓存地实现当中。它的主要优点就是可以跟红黑树、平衡树一样，做到比较稳定地插入、查询与删除。时间复杂度为O(logN)，代码相对简单。

红黑树

一种二叉查找树，每个节点有标记颜色

• 任意的左子树和右子树也分别为二叉查找树，若一节点的左子树不为空，那么左子树上所有节点的值均小于它的根节点的值,右子树同理
• 没有键值相等的节点（键值为节点编号和节点的值）
• 根节点和为空叶子结点都是黑的，如果一个节点是红的，那么它的子节点两是黑的
• 任意一结点到每个叶子结点的路径都包含数量相同的黑结点

B树、B-树、B+树和B*树的区别

• 二叉搜索树：二叉树，每个结点只存储一个关键字，等于则命中，小于走左结点，大于走右结点。
• B-树：多路搜索树，每个节点都会保存数据，关键字只会出现一次。有n棵子树的非叶子结点中含有n-1个关键字。
• B+树：在B-树基础上，为叶子结点增加链表指针，所有数据都保存在叶子结点中，非叶子结点作为叶子结点的索引。有n棵子树的非叶子结点中含有n个关键字，同一个关键字会在不同节点中重复出现。
• B*树：在B+树基础上，为非叶子结点也增加指向兄弟的链表指针，将结点的最低利用率从1/2提高到2/3

B+树的查询优势

• B+树的中间节点不保存数据，所以磁盘页能容纳更多节点元素，更“矮胖”
• B+树查询必须查找到叶子节点，B树只要匹配到即可不用管元素位置，因此B+树查找更稳定，但是速度上并不慢
• 对于范围查找来说，B+树只需遍历叶子节点链表即可，B树却需要重复地中序遍历

数据库-----------------------------------------------------------------

数据库索引的作用

数据库索引是为了增加查询速度而对表字段附加的一种标识。

• 通过创建唯一性索引，可以保证数据库表中每一行数据的唯一性。
• 可以大大加快数据的检索速度，加速表和表之间的连接，特别是在实现数据的参考完整性方面。
• 在使用分组和排序子句进行数据检索时，同样可以显著减少查询中分组和排序的时间。
• 通过使用索引，可以在查询的过程中，使用优化隐藏器，提高系统的性能。

关于索引

应该建索引的字段：

• 经常作为查询条件的字段
• 外键
• 经常需要排序的字段
• 分组排序的字段

应该少建或者不建索引的字段：

• 表记录太少
• 经常需要插入、删除、修改的表
• 表中数据重复且分布平均的字段

mysql的主备模式

保持两个数据库的状态自动同步。对任何一个数据库的操作都自动应用到另外一个数据库，始终保持两个数据库数据一致。

优点：

1. 可以做灾备，其中一个坏了可以切换到另一个。
2. 可以做负载均衡，可以将请求分摊到其中任何一台上，提高网站吞吐量。
3. 读写分离，提供查询业务

数据主从同步一致性解决方案

• 同步复制：指主库执行完一个事务，并且所有从库都执行了该事务才返回给客户端。因为需要等待所有从库执行完该事务才能返回，所以全同步复制的性能必然会收到严重的影响。
• 异步复制：MySQL默认的复制是异步的，主库在执行完客户端提交的事务后会立即将结果返回给客户端，并不关心从库是否已经接收并处理
• 半同步复制：介于异步复制和全同步复制之间，主库在执行完客户端提交的事务后不是立刻返回给客户端，而是等待至少一个从库接收到并写到relay log中才返回给客户端。提高了数据的安全性，同时也造成了延迟，这个延迟最少是一个TCP/IP往返的时间。所以，半同步复制最好在低延时的网络中使用。

程序题

链表

单链表逆序

ListNode* reverseList(ListNode* head) {
	ListNode *cur = head;
    ListNode *tmp, *prev = NULL;
    while (cur) {
    	tmp = cur->next;
        cur->next = prev;
        prev = cur;
        cur = tmp;
    }
    return prev;
}

[LeetCode83] 有序链表去重

struct ListNode {
	int val;
	ListNode *next;
	ListNode(int x) : val(x), next(NULL) {}
};

ListNode* deleteDuplicates(ListNode* head) {
	ListNode *left = head, *right;
	while(left) {
		right = left->next;
		if(right && left->val == right->val) {
			left->next = right->next;
			delete right;
		}
		else left = right;
	}
	return head;
}

二叉树镜像

递归实现：

void MirrorRecursively(TreeNode *pRoot)
{
    if(pRoot == NULL) return;
    TreeNode *pTemp = pRoot->left;
    pRoot->left = pRoot->right;
    pRoot->right = pTemp;
    if(pRoot->left) MirrorRecursively(pRoot->left);  
    if(pRoot->right) MirrorRecursively(pRoot->right); 
}

非递归实现：

void MirrorIteratively(TreeNode* pRoot)
{
	if(pRoot == NULL) return;
	stack<TreeNode*> stk;
	stk.push(pRoot);
	while(!stk.empty()) {
		TreeNode *pNode = stk.top(); stackTreeNode.pop();

		TreeNode *pTemp = pNode->left;
		pNode->left = pNode->right;
		pNode->right = pTemp;

		if(pNode->left) stackTreeNode.push(pNode->left);
		if(pNode->right) stackTreeNode.push(pNode->right);
	}
}

调整一棵二叉树，要求所有节点的右子树的最大值大于左子树的最大值

int maxV(BTNode *root){
	if(root == null) return INF;
    if(maxV(root.left) > maxV(root.right)) swap(root.left, root.right);
    return max(root.v, maxV(root.left), maxV(root.left));
}

二叉树的三序遍历

• 先序

void preOrder2(BinTree *root) {  // 非递归实现前序遍历 
    stack<BinTree*> s;
    BinTree *p = root;
    while(p != NULL || !s.empty()) {
        while(p != NULL) {
            cout << p->data << " ";
            s.push(p);
            p = p->lchild;
        }
        if(!s.empty()) {
            p = s.top(); s.pop();
            p = p->rchild;
        }
    }
}

• 中序

void inOrder2(BinTree *root) {   // 非递归中序遍历
    stack<BinTree*> s;
    BinTree *p = root;
    while(p != NULL || !s.empty()) {
        while(p != NULL) {
            s.push(p);
            p = p->lchild;
        }
        if(!s.empty()) {
            p = s.top(); s.pop();
            cout << p->data <<" ";
            p=p->rchild;
        }
    }    
}

• 后序

vector<int> postOrder(TreeNode *root) {
    vector<int> res;
    if(root == NULL) return res;
    TreeNode *p = root;
    stack<TreeNode *> sta;
    TreeNode *last = root;
    sta.push(p);
    while (!sta.empty()) {
        p = sta.top();
        if((p->left == NULL && p->right == NULL) 
        		|| (p->right == NULL && last == p->left) 
        		|| (last == p->right)) {
            res.push_back(p->val);
            last = p;
            sta.pop();
        }
        else {
            if(p->right) sta.push(p->right);
            if(p->left) sta.push(p->left);
        }
    }
    return res;
}

算法题

16. 随机打乱数组，让概率尽可能相同
17. 代码题，给一个链表，不知道长度，想要随机取一个node，使得每个node被取的概率都是 1/len
18. 实际工程问题，给一些员工，一些project,一些task,每一个task属于一个project，每个员工都可以去任意project里面取任意取任意个task来做，平均每个task需要工作15s， 每一个task的领取时间和提交时间有，现在想询问一个员工一天工作了多长时间。
19. 一个无序数组找其子序列构成的和最大，要求子序列中的元素在原数组中两两都不相邻
20. 现有一个随机数生成器可以生成0到4的数，现在要让你用这个随机数生成器生成0到6的随机数，要保证生成的数概率均匀。
21. 有 N 枚棋子，每个人一次可以拿1到 M 个，谁拿完后棋子的数量为0谁就获胜。现在有1000颗棋子，每次最多拿8个，A 先拿，那么 A 有必胜的拿法吗？第一个人拿完后剩余棋子的数量是8的倍数就必胜，否则就必输。
22. 给出一棵二叉树的根节点，现在有这个二叉树的部分节点，要求这些节点最近的公共祖先。
23. 缺失的第一个正数（leetcode第41题）
24. 求最长上升子序列的个数
25. 非递归遍历二叉树
26. 定一个二叉树，原地将它展开为链表
27. 给定一棵二叉树，想象自己站在它的右侧，按照从顶部到底部的顺序，返回从右侧所能看到的节点值
28. 合并两个有序链表。递归和非递归的实现
    将双向链表按奇偶结点分开，形成两个链表并返回
    如何计算一个包含重复元素的数组中不同元素的个数
    如何利用快排对一个单链表进行排序
    给一个出栈序列长度为n，有多少种入栈的可能
    两个栈模拟队列
    一个二叉树，每个节点除了有左右子节点外，还有指向父节点的引用。给出一个节点，返回它在二叉树中中序遍历的下一个节点。

用rand(5)等概率地生成rand(7)

参考博客：https://blog.csdn.net/u010025211/article/details/49668017

int Rand7(){
    while(x > 21) // x > 7 会导致[8, 25]的数都被浪费掉
        x = 5 * (rand(5) - 1) + rand(5) // x = rand(25)
    return x%7 + 1;
}

用 rand(a) 和 rand(b) 生成 rand(a * b)：

rand(a*b) = a * (rand(b) - 1) + rand(a)

d层楼，e个鸡蛋，最少尝试次数

有一栋楼共100层，一个鸡蛋从第N层及以上的楼层落下来会摔破， 在第N层以下的楼层落下不会摔破。给你2个鸡蛋，设计方案找出N，并且保证在最坏情况下， 最小化鸡蛋下落的次数。(假设每次摔落时，如果没有摔碎，则不会给鸡蛋带来损耗)

	for(int i = 1; i <= d; i++) dp[1][i] = i;
	for(int i = 1; i <= e; i++) dp[i][1] = 1;
	for(int i = 2; i <= e; i++)
	{
		for(int j = 2; j <= d; j++)
		{
			int MIN = 1 + max(dp[i - 1][0], dp[i][j - 1] + 1);
			for(int k = 1; k <= j; k++)
			{
				MIN = min(MIN, 1 + max(dp[i - 1][k - 1], dp[i][j - k]));
			}
			dp[i][j] = MIN;
		}
	}
	printf("%d\n", dp[e][d]);

用2x1型和1x1型两种积木，摆满n行m列，有多少种摆法

提示：先考虑2行m列有多少种摆法，再算n行m列

对于每列来说情况相同，对于搭一列的问题，就是走楼梯问题，一次可以走一步或者两步，总共有多少种走法。

dp[i][0] += dp[i-1][0..3]
dp[i][1] += dp[i-1][0, 2]
dp[i][2] += dp[i-1][0, 1]
dp[i][3] += dp[i-1][0]

两个升序数组，找出第k小的数字

int get_kth_smallest(vector<int>& nums1, int st1, const int& sz1, vector<int>& nums2, int st2, const int& sz2, int k) {
        // 保证nums1.size() <= nums2.size()，方便分析
        if (sz1-st1 > sz2-st2) return get_kth_smallest(nums2, st2, sz2, nums1, st1, sz1, k);
        if (sz1 - st1 == 0) return nums2[k-1 + st2];
        if (1 == k) return nums1[st1] < nums2[st2]? nums1[st1]:nums2[st2];
        
        // 在nums1和nums2中分别取第k/2个数字。如果超出边界，取最后那个数字
        int k1 = min(sz1-st1, k/2);
        int k2 = min(sz2-st2, k/2);
        // 如果nums1[k1-1] < nums2[k2-1]，说明nums1[k1-1]小于要找的第k小
        if (nums1[st1+k1-1] < nums2[st2+k2-1]) return get_kth_smallest(nums1, st1+k1, sz1, nums2, st2, sz2, k-k1);
        // 如果nums1[k1-1] > nums2[k2-1]，说明nums2[k2-1]小于要找的第k小
        // 如果nums1[k1-1] == nums2[k2-1]，说明nums2[k2-1]小于等于要找的第k小。但是依然可以删掉它，因为还有nums1[k1-1]和它相等
        else return get_kth_smallest(nums1, st1, sz1, nums2, st2 + k2, sz2, k-k2);
        }
    }

将数组顺时针旋转90°

// 先按照主对角线反转， 再按照中垂线反转
void rotate(vector<vector<int>>& matrix) {
        int n = matrix.size();
        for (int i = 0; i < n; ++i) {
            for (int j = i + 1; j < n; ++j) {
                swap(matrix[i][j], matrix[j][i]);
            }
            reverse(matrix[i].begin(), matrix[i].end());
        }
    }

二叉树上找LCA

• 有father版：直接求深度， 然后深度大的先跳， 再一起跳。
• 无father版：递归回溯时找到节点就返回给父亲节点，当父亲节点get到了两个点就是答案
• 二叉排序树版， 从树的根结点出发遍历树，如果当前结点都大于输入的两个结点，则下一步遍历当前结点的左子树；如果当前结点小于输入的两个结点，则下一步遍历当前结点的右子树。一直遍历到当前结点比一个输入结点大而比另一个小的时候，此时当前结点就是符合要求的最低公共祖先。

给定一个数组，将所有0元素移动到它的末端，同时保持非零元素的相对顺序

双指针， 从前往后扫即可。

判断一棵二叉树是否是平衡二叉树

满足以下两点的就是平衡二叉树：
1.左右子树的高度差不能超过1
2.左右子树也是平衡二叉树

int IsBalance(BNode *root,int *pHeight) {
	if(root == NULL) { *pHeight = 0; return 1; }
	int leftHeight, rightHeight;
	int leftBalance = IsBalance(root->left, &leftHeight);
	int rightBalance = IsBalance(root->right, &leftHeight);
	*pHeight = max(leftHeight, rightHeight) + 1;
	if(leftBalance == 0 || rightBalance == 0) return 0;
	if(abs(leftHeight - rightHeight) > 1) return 0;
	return 1;
}

一个数组，每个位置的值对应下标。重新排列后要求对应位置上的值不能和下标相同，计算方案数

错排公式：$D[n]=(n-1)\ast (D[n-1]+D[n-2])$，其中$D[1]=0,D[2]=1$，$D[n]$ 表示 n个元素全部错排的方法数。

推导过程：

• 如果现在n - 1个新郎全错排，现在添加一对夫妇，新郎的位置可以任意与n - 1个新郎换都可以达到全错排，有$(n-1)\ast D(n-1)$种情况。
• 如果n - 1个新郎不是全错排，要再添加一对夫妇后实现全错排需要满足：n - 1中只有一个人找到了他的新娘（即n - 2个人实现了全错排），这时只要这个没有错排的人和第n个交换，就会实现全错排。由于找到新娘的这个人可以是n-1其中任意一位，所以一共有(n - 1) * D(n - 2)种情况
• 综上情况相加：故D[n] = (n - 1) * (D[n - 1] + D[n - 2])

输出k对括号的全部正确匹配方案

• k = 1时，一个括号只有一种可能，就是（）
• k = 2时，可以在1的基础上在其左边加一对括号、在右边加一对括号或者加的括号包住1，即()()、()()、(())，去掉重复就剩下两种

set<string> solve(int n) {
	set<string> s; // 用set去重
	if(n == 1) {
		s.add("()");
		return s;
	}
	else {
		set<string> s2 = solve(n - 1);
		for(string now : set2) {
			s.add("()" + now);
			s.add(now + "()");
			s.add("(" + now + ")");
		}
		return s;
	}
}

将一些柱子整齐的立在一行，高度存在数组height[]中，然后往凹下去的地方倒水，问一共能蓄多少单位水

比如[5,1,3,4,5,1,3]，答案是7 + 2 = 9
维护每一个柱子左右的最高柱子， 当前柱子的存水量就是 min(左最大值， 右最大值)。

[POJ 2796] 求一个区间，使得区间和乘以区间最小值最大

单调栈 扫两遍

设计一个类，只能生成该类的一个实例

public class Singleton{
	private static Singleton instance = null;
	private(){
	}
	public static Singleton getInstance(){
		if(instance = null) {
			instance = new Singleton();
		}
		return instance;
	}
}

求数组中逆序对

归并排序

//参考紫书算法竞赛入门经典 
void merge_sort(int *A, int l, int r, int *T){ //[l, r) 排序. 外部调用区间为[0, n)
	if(r - l > 1){
		int mid = l+(r-l)/2;
		int p = l, q = mid, now = l;
		// 对左右两部分区间分别归并排序
		merge_sort(A, l, mid, T); 
		merge_sort(A, mid, r, T);
		// 合并左右两部分
		while(p < mid || q < r){
			if(q >= r ||  (p < mid && A[p] <= A[q])){
				T[now++] = A[p++];
			}
			else{
				T[now++] = A[q++];
				cnt += mid - p; // cnt记录的是逆序对个数
			}
		}
		for(int i = l; i < r; i++) A[i] = T[i];
	}
}

快速排序的稳定化算法

• 普通快速排序

#include 
 
using namespace std;
 
void Qsort(int a[], int low, int high)
{
    if(low >= high) return;
    int first = low;
    int last = high;
    int key = a[first];/*用字表的第一个记录作为枢轴*/
 
    while(first < last)
    {
        while(first < last && a[last] >= key) last--;
        a[first] = a[last];/*将比第一个小的移到低端*/
        while(first < last && a[first] <= key) first++;
        a[last] = a[first];    
/*将比第一个大的移到高端*/
    }
    a[first] = key;/*枢轴记录到位*/
    Qsort(a, low, first-1);
    Qsort(a, first+1, high);
}
int main()
{
    int a[] = {57, 68, 59, 52, 72, 28, 96, 33, 24};
 
    Qsort(a, 0, sizeof(a) / sizeof(a[0]) - 1);/*这里原文第三个参数要减1否则内存越界*/
 
    for(int i = 0; i < sizeof(a) / sizeof(a[0]); i++)
    {
        cout << a[i] << "";
    }
     
    return 0;
}/*参考数据结构p274(清华大学出版社，严蔚敏)*/

• 稳定方法

100w个数 找最大top100

用小根堆维护， 当前值大于队内最小值就替换。

堆排序

• 堆排序是利用堆这种数据结构而设计的一种排序算法，堆排序是一种选择排序，它的最坏，最好，平均时间复杂度均为O(nlogn)，它也是不稳定排序。首先简单了解下堆结构。

include 
#include 
using namespace std;
 
void max_heapify(int arr[], int start, int end) {
    //建立父节点指标和子节点指标
    int dad = start;
    int son = dad * 2 + 1;
    while (son <= end) { //若子节点指标在范围内才做比较
        if (son + 1 <= end && arr[son] < arr[son + 1]) //先比较两个子节点大小，选择最大的
            son++;
        if (arr[dad] > arr[son]) //如果父节点大於子节点代表调整完毕，直接跳出函数
            return;
        else { //否则交换父子内容再继续子节点和孙节点比较
            swap(arr[dad], arr[son]);
            dad = son;
            son = dad * 2 + 1;
        }
    }
}
 
void heap_sort(int arr[], int len) {
    //初始化，i从最後一个父节点开始调整
    for (int i = len / 2 - 1; i >= 0; i--)
        max_heapify(arr, i, len - 1);
    //先将第一个元素和已经排好的元素前一位做交换，再从新调整(刚调整的元素之前的元素)，直到排序完毕
    for (int i = len - 1; i > 0; i--) {
        swap(arr[0], arr[i]);
        max_heapify(arr, 0, i - 1);
    }
}
 
int main() {
    int arr[] = { 3, 5, 3, 0, 8, 6, 1, 5, 8, 6, 2, 4, 9, 4, 7, 0, 1, 8, 9, 7, 3, 1, 2, 5, 9, 7, 4, 0, 2, 6 };
    int len = (int) sizeof(arr) / sizeof(*arr);
    heap_sort(arr, len);
    for (int i = 0; i < len; i++)
        cout << arr[i] << ' ';
    cout << endl;
    return 0;
}

Partition方法求数组第k大的数

#include 
 
using namespace std;
 
int Partition(int* A,int left,int right){
    int key=A[left];
    while(left=key)
            right--;
        if(left

约瑟夫环

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-MHAKF7vd-1585387853397)(/Users/dreamstart/Downloads/media/15516222282812.jpg)]

从1到n整数中1出现的次数

class Solution {
public:
    int countDigitOne(int n) {
        long long base = 1;
        int count = 0;
        while(base <= n){
            int round = n / (base * 10);
            int now = n / base % 10;
            int after = n % base;
            count += round * base;
            if(now == 1) count += after + 1;
            else if(now >= 2) count += base;
            base *= 10;
        }
        return count;
    }
};

le(left while(left=key)
right–;
if(left

    while(left

}

int findKthNum(int* A,int left,int right,int k){
int index=Partition(A,left,right);
if(index+1==k)
return A[index];
else if(index+1 findKthNum(A,index+1,right,k);
else
findKthNum(A,left,index-1,k);
}

int main()
{
int A[]={2,3,5,1,6,7,4};
int len=sizeof(A)/sizeof(A[0]);

cout << findKthNum(A,0,len-1,7) << endl;
return 0;

}

#### 约瑟夫环

[外链图片转存中...(img-MHAKF7vd-1585387853397)]

#### 从1到n整数中1出现的次数

```c++
class Solution {
public:
    int countDigitOne(int n) {
        long long base = 1;
        int count = 0;
        while(base <= n){
            int round = n / (base * 10);
            int now = n / base % 10;
            int after = n % base;
            count += round * base;
            if(now == 1) count += after + 1;
            else if(now >= 2) count += base;
            base *= 10;
        }
        return count;
    }
};

LeetCode

[LeetCode76] 最小覆盖子串：滑动窗口

在字符串 S 里面找出，包含 T 所有字母的最小子串。

string minWindow(string s, string t) {
	int S = s.size() - 1, T = t.size();
	for(int i = 0; i < T; i++) vis[t[i]]++;
	int l = 0, r = -1, cnt = 0, ans = S + 1, ansl = 0, ansr = -1;
	while(l <= S) {
		while(r < S && cnt < T) {
			r++;
			if(tmp[s[r]] < vis[s[r]]) cnt++;
			tmp[s[r]]++;
		}
		if(cnt == T && r - l + 1 <= ans) ans = r - l + 1, ansl = l, ansr = r;
		if(tmp[s[l]] <= vis[s[l]]) cnt--;
		tmp[s[l]]--;
		l++;
	}
	string str = "";
	for(int i = ansl; i <= ansr; i++) str += s[i];
	return str;
}

[LeetCode] Longest Increasing Path in a Matrix

[LeetCode面试题32I II III] 从上到下打印二叉树

• 同一层的节点按照从左到右的顺序打印。

// 按层 BFS即可
class Solution {
public:
    vector<int> levelOrder(TreeNode* root) {
        vector<int> ans;
        if(root == NULL) return ans;
        queue<TreeNode*> que;
        TreeNode *cur = root;
        que.push(cur);
        while(!que.empty()) {
            cur = que.front(); que.pop();
            ans.push_back(cur->val);
            if(cur->left) que.push(cur->left);
            if(cur->right) que.push(cur->right);
        }
        return ans;
    }
};

• 同一层的节点按从左到右的顺序打印，每一层打印到一行

// BFS 过程中特殊处理每一行的节点
class Solution {
public:
    vector<vector<int>> levelOrder(TreeNode* root) {
        vector<vector<int> > ans;
        if(root == NULL) return ans;
        TreeNode *cur = root;
        queue<TreeNode*> que;
        que.push(cur);
        while(!que.empty()) {
            vector<int> now;
            int S = que.size(); // que.size() 就是当前深度的节点数
            for(int i = 0; i < S; i++) {
                cur = que.front(); que.pop();
                now.push_back(cur->val);
                if(cur->left) que.push(cur->left);
                if(cur->right) que.push(cur->right);
            }
            ans.push_back(now);
        }
        return ans;
    }
};

• 按照之字形顺序打印二叉树：reverse一下即可