笔记:有限自动机
有限自动机(Finite Automaton-FA)又可以分为确定的有限自动机(Deterministic Finite Automaton-DFA)和非确定的有限自动机(Nondeterministic Finite Automaton-NFA)。
1.确定的有限自动机DFA
DFA是一个具有离散输入、输出的数学模型。一直一个DFA M表示为:
M=(Q, E, f, q0, Z)
其中:Q为状态的有限集合,每一个元素成为一个状态;E为输入字符的有限集合,每个元素是一个输入字符;f是状态转换函数,是Q叉乘E到Q的映射;q0是M的唯一初态,q0属于Q;Z是M的终态集。
例子:
#确定的有限自动机M=({0,1,2,3},{a,b},f,0,{3})
#其中f为: f(0,a) = 1, f(0,b) = 2
# f(1,a) = 3, f(1,b) = 2
# f(2,a) = 1, f(2,b) = 3
# f(3,a) = 3, f(3,b) = 3上述M所对应的状态图和装填表如下:
识别字符串
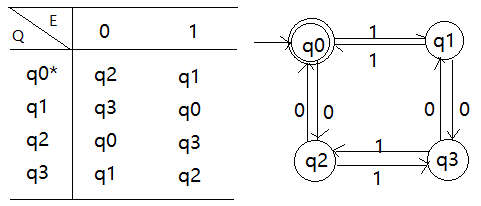
下图为能识别含偶数个0和偶数个1的字符串的DFA M1的双填表和状态图:
由此可以推出M1的形式定义:
#确定的有限自动机M=({q0,q1,q2,q3},{0,1},f,q0,{q0})
#其中f为: f(q0,0) = q2, f(q0,1) = q1
# f(q1,0) = q3, f(q1,1) = q0
# f(q2,0) = q0, f(q2,1) = q3
# f(q3,0) = q1, f(q3,1) = q2任意给出一个函偶数个1和偶数个0的字符串$1=110101,则M对$1的识别过程如下:
f(q0,1) = q1
f(q0,11) = f(f(q0,1),1) = f(q1,1) = q0
f(q0,110) = f(f(q0,11),0) = f(q0,1) = q2
f(q0,1101) = f(f(q0,110),1) = f(q2,1) = q3
f(q0,11010) = f(f(q0,1101),0) = f(q3,1) = q1
f(q0,110101) = f(f(q0,11010),1) = f(q1,1) = q0(q0为终态)有一条从初态节点q0到终态节点q0的路径q0q1q0q2q3q1q0这条路径上所有的弧的标记连接成字符串$1.
2.非确定有限自动机NFA
NFA是一个五元组:
M=(Q, E, f, q0, Z)
其中:Q为状态的有限集合;E为输入字符的有限集合(又穷字母表);f是状态转换函数;q0是M初态;Z是M的终态集。
NFA从一状态节点出发可以有不止一条统一标记的弧。
例子:
#确定的有限自动机M=({q0,q1,q2,q3,q4},{0,1},f,q0,{q2,q4})
#其中f为: f(q0,0) = {q0,q3}, f(q0,1) = {q0,q1}
# f(q1,0) = %(空), f(q1,1) = {q2}
# f(q2,0) = {q2}, f(q2,1) = {q2}
# f(q3,0) = {q4}, f(q3,1) = %(空)
# f(q4,0) = {q4}, f(q4,1) = {q4}上述的NFA M装填表和状态图可表示为:
其找到$1=010110的路径还是只有一条q0q0q0q1q2q2.