pytorch入门（一）：regression回归

回归问题，即：通过分析一组带有因变量和自变量的样本，得出因变量和自变量之间的关系。本文介绍一个最简单的回归问题。并使用神经网络进行分析。

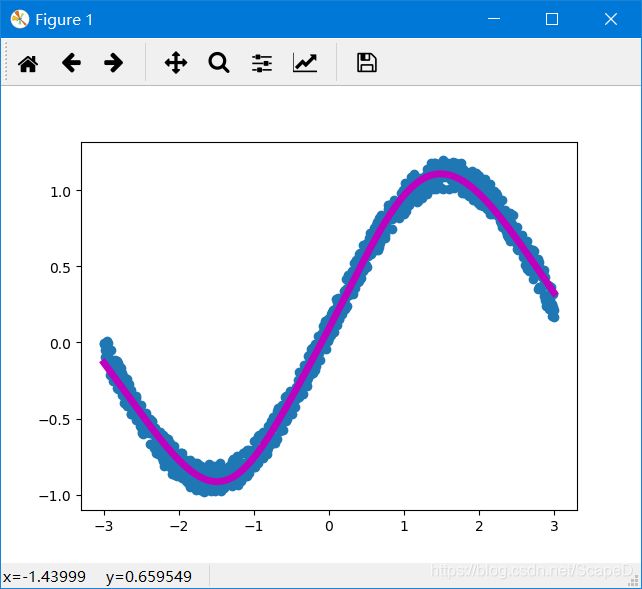
效果图：

介绍 

逐句代码讲解

一、生成样本数据

x=torch.unsqueeze(torch.linspace(-3,3,1000),dim=1)
y=x.sin()+0.2*torch.rand(x.size())

其中torch.unsqueeze()为数据提升维度：

由[1,2,3,4]变为[[1],[2],[3],[4]];神经网络只接受第二种形式的输入数据。

x生成-3到3范围的等间隔的1000个数据；y是x的函数

二、搭建神经网络

class Net(torch.nn.Module):
    def __init__(self,nfeature,n_hidden,n_output):
        super(Net, self).__init__()
        self.hidden=torch.nn.Linear(nfeature,n_hidden)
        self.predict=torch.nn.Linear(n_hidden,n_output)

    def forward(self,x):
        x=torch.tanh(self.hidden(x))
        x=self.predict(x)
        return x

网络以类的形式搭建，必须继承 torch.nn.Module; 其中两个主要函数构造函数__init__()，以及前向传播函数forward()

nfeature,n_hidden,n_output代表：输入数据、隐含层神经元个数、输出层，其中隐含层神经元个数=隐含层输出值个数

 super(Net, self).__init__()这句规定必写

        self.hidden=torch.nn.Linear(nfeature,n_hidden) 定义隐含层
        self.predict=torch.nn.Linear(n_hidden,n_output)定义输出层

    def forward(self,x):中x代表输入值

x=torch.tanh(self.hidden(x))  其中self.hidden(x)代表以神经网络hidden层处理输入值，torch.tanh(）代表将上述值用激活函数tanh再进行处理。

x=self.predict(x)代表以神经网络predict层处理x输出

三、创建优化器

神经网络搭建好了，要想进行学习，必须经过优化的过程

optimizer=torch.optim.SGD(net.parameters(),lr=0.1)
loss_func=torch.nn.MSELoss()

optimizer=torch.optim.SGD(net.parameters(),lr=0.1)指定优化器为SGD，输入网络参数，学习率设置为0.1

损失函数设置为MSELoss均方根损失，为回归问题常用方法 

四、模型训练

for t in range(10000):
    prediction=net(x)

    loss=loss_func(prediction,y)

    optimizer.zero_grad()
    loss.backward()
    optimizer.step()

模型训练10000轮， 

prediction=net(x)使用模型预测数据

loss=loss_func(prediction,y)计算损失（误差）

最后：  梯度清零（清除上一轮残留的梯度）、损失反馈、优化器根据梯度进行优化：

  optimizer.zero_grad()
    loss.backward()
    optimizer.step()  

全部代码：

import torch
import matplotlib.pyplot as plt

x=torch.unsqueeze(torch.linspace(-3,3,1000),dim=1)
y=x.sin()+0.2*torch.rand(x.size())

class Net(torch.nn.Module):
    def __init__(self,nfeature,n_hidden,n_output):
        super(Net, self).__init__()
        self.hidden=torch.nn.Linear(nfeature,n_hidden)
        self.predict=torch.nn.Linear(n_hidden,n_output)

    def forward(self,x):
        x=torch.tanh(self.hidden(x))
        x=self.predict(x)
        return x

net=Net(1,10,1)
print(net)

plt.ion()
plt.show()

optimizer=torch.optim.SGD(net.parameters(),lr=0.1)
loss_func=torch.nn.MSELoss()

for t in range(10000):
    prediction=net(x)

    loss=loss_func(prediction,y)

    optimizer.zero_grad()
    loss.backward()
    optimizer.step()

    if t%5==0:
        plt.cla()
        plt.scatter(x,y)
        plt.plot(x,prediction.data.numpy(),'m',lw=5)
        plt.pause(0.1)

plt.ioff()
plt.show()

参考：

[1]Regression回归https://www.bilibili.com/video/BV1Vx411j7kT?p=11

[2]回归问题的解释https://www.zhihu.com/question/21329754