AGC010 - C: Cleaning

原题链接

题意简述

给出一棵 n(n≤105) 个节点的树，每个点有点权。每次可以选择两个叶节点并将连接它们的路径上的节点的点权-1（包括叶节点）。求能否将所有节点的点权都变为0。

分析

先考虑最简单的情况。在这种情况下， au 必须等于 av ，否则GG。因为要想对v操作只能通过u，想对u操作只能通过v。
若相等我们可以令 bu=av ，并定义 bu 为：u需要往外连 bu 条路径。因为需要有 au 条路径进到以u为根的子树里面，可以看做u需要向外连 au 条路径。

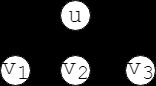
再考虑一般情况。在这种情况下， au 必须小于等于 ∑bv ，否则GG。因为即使把 bv 都减完了 au 也不能为0，并且已经没有办法再减少 au 了。
若 au=∑bv ，直接从u往外连 au 条路径就好了。
和刚才不同，v之间可以自行解决一部分。比如操作 v1−u−v2 ，可以让 bu 减1，让 ∑bv 减2。我们可以进行类似的操作直到 bu=∑bv ，然后同上。
但是有可能没法让 bu=∑bv ，那就GG。那什么情况下不可行呢？
结论：当 max{bv}≤(∑bv)/2 时，可以把所有的 bv 消成0（或者剩一个1）。

证明

可能不对，看看就好

我们可以把问题反转一下：
对于一个零序列，每次对两个位置+1，能否得到目标序列？
显然的结论有当 max{bv}>(∑bv)/2 时会有 max{bv}−(∑bv−max{bv}) 加不出来。以及当 ∑bv 为奇数时至少会剩下一个。
下证对于其他情况：
额外创建两个位置，对它们进行无限次操作，意思就是足够多次。
{0,0,...,0} -> {0,0,...,0(,inf,inf)}
这时候我们加入了一种新操作：令这两个 inf 减1，也就是撤回一次。 然后我们可以做到 :
{0,0,...,0(,inf,inf)} -> {1,0,...,0(,inf+1,inf)} -> {2,0,...,0(,inf+1,inf+1)} -> {2,0,...,0(,inf,inf)} 。
这样就有了构造方法：先两两给所有奇数填上1（要是有奇数个奇数就说明 ∑bv 为奇数肯定会剩下，所以可以把一个奇数视为偶数），然后通过以上+2的操作把所有数都填好。最后对额外的两个位置一直-1减到0，这样就构造完成了。

如果在任何时候出现 bu 无法等于 ∑bv ，那么GG。
以及， broot≠0 也GG。
遍历所有节点复杂度为 O(n) ，遍历每个节点的所有子节点复杂度为 O(n) ，总时间复杂度为 O(n) 。

实现

首先以一个度不为1的点作为 root ，然后DFS出深度 dpt 和树的结构
由下到上将节点u和它的子节点v合并出 bu ，最后检查 broot

代码

//Cleaning
#include 
#include 
#include 
using namespace std;
typedef long long lint;
int const N=1e5+10;
int n,a[N];
int cnt,h[N],deg[N];
struct edge{
    int u,v,nxt;
    edge(int u1=0,int v1=0)
    {
        u=u1,v=v1;
        nxt=h[u];
        h[u]=cnt;
    }
}ed[N<<1];
int root,fa[N],dpt[N];
struct rec{int dpt,id;} r[N];
bool cmpDpt(rec x,rec y) {return x.dpt>y.dpt;}
void dfs(int u)
{
    for(int i=h[u];i!=0;i=ed[i].nxt)
    {
        int v=ed[i].v;
        if(v==fa[u]) continue;
        fa[v]=u,dpt[v]=dpt[u]+1;
        dfs(v);
    }
}
int main()
{
    freopen("c.in","r",stdin);
    scanf("%d",&n);
    for(int i=1;i<=n;i++) scanf("%d",&a[i]);
    if(n==2)
    {
        if(a[1]!=a[2]) printf("NO");
        else printf("YES");
        return 0;
    }
    cnt=0; memset(h,0,sizeof h);
    for(int i=1;i<=n-1;i++)
    {
        int u,v;
        scanf("%d%d",&u,&v);
        ed[++cnt]=edge(u,v); deg[v]++;
        ed[++cnt]=edge(v,u); deg[u]++;
    }
    for(int i=1;i<=n;i++)
        if(deg[i]>1)
        {
            fa[i]=0,dpt[i]=1;
            dfs(root=i);
            break;
        }
    for(int i=1;i<=n;i++) r[i].dpt=dpt[i],r[i].id=i;
    sort(r+1,r+n+1,cmpDpt);
    for(int i=1;i<=n;i++)
    {
        int u=r[i].id;
        if(deg[u]==1) continue;
        int maxx=0; lint sum=0;
        for(int j=h[u];j!=0;j=ed[j].nxt)
        {
            int v=ed[j].v;
            if(fa[v]!=u) continue;
            maxx=max(maxx,a[v]); sum+=a[v];
        }
        lint in=min(sum/2,sum-maxx);
        if(a[u]>sum) {printf("NO"); return 0;}
        else
        {
            if(sum-a[u]>in) {printf("NO"); return 0;}
            else a[u]-=sum-a[u];
        }
    }
    if(a[root]==0) printf("YES");
    else printf("NO");
    return 0;
}

注意

n=2 时要特判一下，因为两个点都是叶节点会找不出 root