2020 杭电多校 G题 Go Running（二分图匹配 dinic）

思路

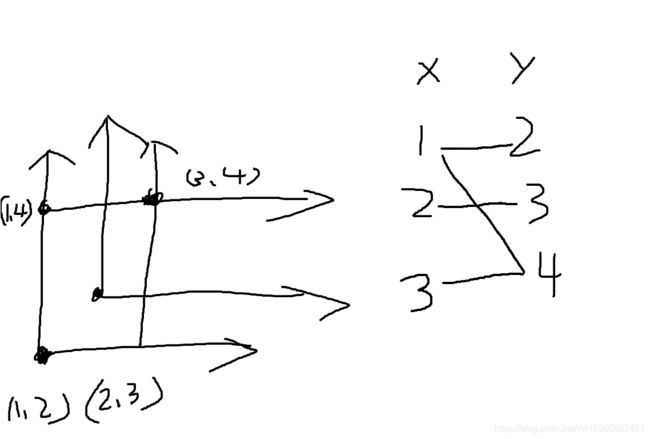
画个x-t图，画出两个斜率的直线，逆时针旋转45度，可以变成如图所示的图形。

我们将x和y分别作为二分图的两个集合跑最小点覆盖即可。

最小点覆盖等于最大匹配

数据为1e5，套dinic板子即可。

自己没有总结dinic板子，代码是参考别人的，见文末链接。

这道题比较奇特的是，将两个方向的直线，变成二分图匹配中的点。将题目中的点，变成了二分图匹配的边。

将 用最少直线覆盖所有点 变成了 二分图中的最少点覆盖所有边，即最小点覆盖问题。

代码

#include 
using namespace std;
typedef long long ll;
const int maxn = 5e5 + 10;
const int INF = 0x3f3f3f3f;
vector <int> v1, v2;
struct edge{
    int to, next, cap;
}e[maxn * 2];
int n, maxflow, cnt, s, t;
int x[maxn], y[maxn], h[maxn], cur[maxn], dep[maxn];
void add(int u, int v, int cap){
    e[cnt].to = v;
    e[cnt].cap = cap;
    e[cnt].next = h[u];
    h[u] = cnt++;

    e[cnt].to = u;
    e[cnt].cap = 0;
    e[cnt].next = h[v];
    h[v] = cnt++;
}
bool bfs(){
    for (int i = 0; i <= t; i++)
        dep[i] = -1, cur[i] = h[i];
	queue <int> q;
	q.push(s);
	dep[s] = 0;
	while (q.size()) {
		int u = q.front();
		q.pop();
		for (int i = h[u]; ~i; i = e[i].next) {
			int v = e[i].to;
			if (e[i].cap && dep[v] == -1) {
				dep[v] = dep[u] + 1;
				q.push(v);
			}
		}
	}
	if (dep[t] >= 0)
        return true;
	else
        return false;
}
int dfs(int u, int mx){
    int a;
    if(u == t)
        return mx;
    for(int i = cur[u]; ~i; i = e[i].next){
        cur[u] = i;
        int v = e[i].to;
        if(e[i].cap && dep[v] == dep[u] + 1 && (a = dfs(v, min(e[i].cap, mx)))){
            e[i].cap -= a;
            e[i ^ 1].cap += a;
            return a;
        }
    }
    return 0;
}
void dinic(){
    int res;
    while(bfs()){
        while(1){
            res = dfs(s, INF);
            if(!res)
                break;
            maxflow += res;
        }
    }
}
void init(){
    v1.clear();
    v2.clear();
    maxflow = cnt = 0;
}
int main(){
    int T; scanf("%d", &T);
    while(T--){
        scanf("%d", &n);
        init();
        for(int i = 0, a, b; i < n; i++){
            scanf("%d %d", &a, &b);
            x[i] = a + b, y[i] = a - b;
            v1.push_back(x[i]), v2.push_back(y[i]);//可以不用乘
        }
        sort(v1.begin(), v1.end());
        sort(v2.begin(), v2.end());
        v1.erase(unique(v1.begin(), v1.end()), v1.end());
        v2.erase(unique(v2.begin(), v2.end()), v2.end());

        int len = v1.size();
        s = 0, t = v1.size() + v2.size() + 1;
        for(int i = 0; i <= t; i++) h[i] = -1;
        for(int i = 1; i <= len; i++) add(s, i, 1);
        for(int i = 0; i < n; i++){
            x[i] = lower_bound(v1.begin(), v1.end(), x[i]) - v1.begin() + 1;
            y[i] = lower_bound(v2.begin(), v2.end(), y[i]) - v2.begin() + 1;
            add(x[i], y[i] + len, 1);
        }
        for(int i = len + 1; i <= t - 1; i++) add(i, t, 1);
        dinic();
        printf("%d\n", maxflow);
    }
	return 0;
}

参考来源

链接