图论一图论基础
Graph theory:
In mathematics, graph theory is the study of graphs, which are mathematical structures used to model pairwise relations between objects. A graph in this context is made up of vertices (also called nodes or points) which are connected by edges (also called links or lines). A distinction is made between undirected graphs(无向图), where edges link two vertices symmetrically, and directed graphs(有向图), where edges link two vertices asymmetrically.
上面是节选自Wikipedia的关于图论的定义,对图的定义的十分清晰。图论作为数学的一个分支已经发展了数百年的历史了,前人们发现了很多图的需要重要且实用的性质,发明了许多重要的算法,时至今日,仍然有许多困难的问题的研究十分活跃。我们会先从图,论基础开始慢慢的深入图论,讨论图论的一些性质,讨论和图论的一些关联的实际问题,并试图用算法解决。为了展示图论应用的广泛领域,我们在踏入这片富饶之地之前先看看几个和图相关的几个实例。
地图。对于想要陆行的人可能想知道城市A到城市B的哪条路径的距离最短?对于经历过交通堵塞的人们可能想知道从城市B哪条路线的用时最短?解决这些问题,就需要处理节点(十字路口)之间多条连接(公路)的信息。
计算机网络。计算机网络是由能够发送、转发、接收的站点互相连接组成的。我们感兴趣的是这种互联结构的性质,因为我们希望网络中的线路和交换设备能够高效地处理网络流量。
社交网络。使用社交网络时,你和你的好友、家人建立起明确的关系。在社交网络中,节点是每一个个体,而连接则是把各个个体连接起来。分析这些社交网络的性质是图论算法的一个重要应用领域(据说十年前对图论有研究的程序员在Facebook十分吃香 ^_^)。
图论中包含四种重要的图模型:无向图(简单连接)、有向图(连接带有方向性)、加权图(连接带有价值)和加权有向图(连接既有方向又有价值)。我们将从无向图开始进入图论的学习,并在无向图中介绍图中的血多重要概念和定义。这些定义对于我们理解图的性质和运用图进行工程问题求解是十分有帮助的。
-
无向图
定义:图是由一组顶点和一组能够把顶点连接起来的边组成。我们做一个约定,使用1到V表示顶点1到顶点V,这样的约定便于我们使用数组索引图中的顶点,从而能够编写出高效访问节点信息的代码。在绘制图时,通常用圆圈表示顶点,用连接两个顶点的线段表示边,这样就能直观的看出图的结构来,但图的定义和图的描绘是无关的。
关于图的定义会有两种特殊情况。①自环边:及一条连接一个顶点及其自身的一条边。②平行边:连接同一对顶点的两条边称之为平行边。数学家们通常把拥有平行边的图称之为多重图,把不拥有平行边的图称之为简单图。下图是一个包含自环边和平行边的图。
- 图的概念、定义
和图相关的术语非常多,在这里给出关于图的绝大部分定义。
定义:当两个顶点通过一条边相连时,我们称这两个顶点是相邻的,并称这条边依附于这两个顶点。顶点的度数即为和它相连的边的总数。子图是一幅图的所有边的一个子集(以及他们所依附的所有顶点)组成的图。
定义:在图中,路径是由边顺序连接的一些顶点。简单路径是一条没有重复顶点的路径。环是一条至少含有一条边并且起点和终点相同的路径(只有一条边的环称之为自环边)。简单环是一条(除了起点和终点必须相同之外)不含有重复顶点和边的环。路径或环的长度是其包含的边数。
当两个顶点之间存在一条连接双方的路径时,我们称一个顶点和另一个顶点是相连的。我们使用u-v-w-x的记号表示从顶点u到顶点x的一条路径,用u-v-w-x-u表示一条从u到v到w到x再回到u的环。
定义:如何从图中的任意一个顶点都存在一条路径到达图中的另一个任意顶点,我们称该图是连通图。非连通的图由若干连通的部分组成,他们都是其最大连通子图。
定义:树是一副无环连通图。互不相连的树组成了森林。连通图的生成树是它的一副子图,生成树含有图中的所有顶点且是一颗树。图的生成森林是它的所有连通子图的生成树的集合。
当一个含有V个顶点的图G包含下列五个条件之一时,它就是一棵树。树中的很多性质和算法能够辅助解决的图论中的很多问题。
- G有V-1条边并且不包含环;
- G有V-1条边并且是连通的;
- G是连通的,但是删除任意一条边都会使得图G不再是连通的;
- G是无环图,但是添加任意一条边在图G中都会形成环;
- G中的任意一对顶点之间仅存在一条简单路径;
图的密度是指已经连接的顶点对占理论上可能的顶点对的比例。在稀疏图中,被连接的顶点对很少;在稠密图,被连接的顶点对较多;图的密度关系到我们使用到什么样的数据结构表示图。二分图是一种能将所有顶点分成两部分的图,其中图的每一条边所连接的两个顶点都分别属于不同的部分。大致介绍了一些图的定义和概念,接下来就从无向图开始进行图的讨论。
- 无向图的表示
图的表示方式。对于实现图的数据结构,要满足两个要求:
- 它必须为可能的应用中碰到的各种类型的图预留足够的空间;
- 实现图的数据结构一定要快——他们是处理各种图的问题的基础。
常用的实现图的方式:
- 邻接表数组。我们使用一个以顶点为索引的列表数组,数组的每个元素都是一个记录了和该顶点相邻的边的线性表。(如图)
- 邻接矩阵。我们使用V*V的布尔矩阵。当顶点v和顶点w之间有连接的边时,定义v行w列的元素值为true,否则为false。这种方式通常用于表示数量较小的稠密图,如果顶点数目过大则不适合,因为需要开辟(V*V的空间)。
非稠密图的标准表示是使用邻接表的数据结构,它将每个顶点的所有相邻的顶点都保存在一个链表中(也可以保存每个顶点相邻的边)。我们可以使用数组很快的定位到顶点对应的链表,并且遍历链表就能知道和顶点连接的顶点。下面给出一个基于邻接表的稀疏图的实现。
//该图的实现保证不包含自环边和平行边
public class SparseGraph implements Graph {
/*图的节点个数*/
private int m;
/*图包含的边数目*/
private int n;
/*该图是有向图还是无向图*/
private boolean directed;
/*使用邻接表表示每个节点相连的顶点*/
private LinkedList[] graph;
/**
* 根据传入的边数目构造图,
* @param m
* @param directed true表示有向图,false表示无向图
*/
public SparseGraph(int m,boolean directed){
this.m = m;
this.n = 0;
this.directed = directed;
//graph表示的邻接表中,0表示没有边,1表示有边.
graph = ( LinkedList< Integer > []) new LinkedList [m];
for (int i = 0; i < m; i++) {
graph[i] = new LinkedList();
}
}
/*返回节点数目*/
public int V(){
return this.m;
}
/*返回边数目*/
public int E(){
return this.n;
}
/*在节点v和节点w之间建立起一条边,v,w 都是[1....m],而索引则是[0....m-1]*/
public void addEdge(int v,int w){
if(hasEdge(v,w) || v == w){
return;
}
graph[v-1].add(w);
if(!directed && v != w){ //处理自环边
graph[w-1].add(v);
}
n++;
}
/*两个顶点之间是否相连*/
public boolean hasEdge(int v,int w){
return graph[v-1].contains(w);
}
/*返回和顶点v相连的顶点*/
public Iterator adj(int v){
return graph[v-1].iterator();
}
/*计算边v的度,v=[1......V]*/
public int degree(int v){
return graph[v-1].size();
}
/*计算图中最大的度数*/
public int maxDegree(){
int max = degree(1);
for (int i = 2; i <= V() ; i++) {
if(max < degree(i)) max = degree(i);
}
return max;
}
}
- 广度优先搜索
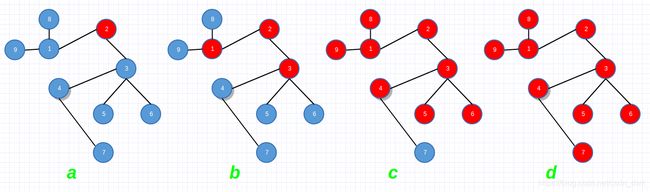
广度优先搜索是最简单的图的搜索算法之一,也是许多图的算法的原型。求解图的最小生成树的Prim算法和求解单源最短路径的Dijkstra算法都使用了类似于广度优先搜索的思想。对于给定的图G=(V,E)和源顶点s,广度优先搜索对图G的所有边进行系统性的探索来发现尽可能多的顶点。该算法能计算从源节点s到达所有能到达的顶点的距离(边数最少),同时生成一棵广度优先树。该树以源节点s为根节点,包含所有能从源节点s到达的节点。对于任意的可达到节点w,广度优先搜索算法能够找到一条路径最短的路径。该算法可用于有向图,也可用于无向图。广度优先搜索在搜索图中的顶点时,总是会搜索完所有距离源顶点s的路径为k的顶点后才会乡下继续搜索所有到源顶点距离为k+1的顶点。下图展示了从源顶点2进行广度优先搜索整张图的过程,被涂色为红色表示已经被访问,被涂色为蓝色表示尚未被访问。在图a中,最初只有源节点2被访问,从源顶点2进行广度优先搜索,也就是搜索距离源顶点2的距离为1的这些顶点(图b)。搜索完距离源顶点为1的顶点后搜索距离源顶点距离为2的顶点(图c),在图d中,距离源顶点距离为3的顶点7也被访问,广度优先搜索完成。
实现广度优先搜索算法:为了实现图的广度优先算法,我们需要借助队列来暂存访问到的顶点。对于源顶点2,一次访问距离源顶点2的距离为1的顶点1、3。并将顶点1 、3加入到队列中,当访问距离源顶点距离为1的顶点后,这些顶点都被暂存到了队列中,然后依次遍历队列中的顶点的相邻的顶点,如果相邻的顶点未被访问则加入到队列,最后当队列为空时,从源顶点2出发的所有可以到达的顶点全部被访问。
public class BFS {
/*源顶点*/
private int source;
/*搜索的图*/
private Graph graph;
/*记录顶点是否被访问*/
private boolean[] visited;
/*当前顶点的前继顶点*/
private int[] from;
/*源顶点到顶点v的路径长度*/
private int[] order;
public BFS(Graph graph, int source){
int m = graph.V();
this.from = new int[m];
this.order = new int[m];
this.visited = new boolean[m];
this.graph = graph;
this.source = source;
for (int i = 0; i < m; i++) {
from[i] = -1;
order[i] = -1;
visited[i] = false;
}
/*进行广度优先遍历*/
LinkedList queue = new LinkedList<>();
queue.add(source);
visited[source-1] = true;
order[source-1] = 0;
while (!queue.isEmpty()){
int q = queue.removeFirst();
Iterator iterator = graph.adj(q);
/*遍历当前顶点的相邻顶点,如果相邻顶点没被访问则加入到队列,并记录from和order数组*/
iterator.forEachRemaining(integer -> {
if(!visited[integer-1]){ //还没有被添加到队列中
visited[integer-1] = true;
queue.add(integer);
from[integer-1] = q;
order[integer-1] = order[q-1]+1;
}
});
}
}
/*考察在图中source和w是否有路径,如果有路径,那么从source进行广度优先搜索是就访问到了w*/
public boolean hashPath(int w){
return visited[w-1];
}
/*返回源节点到节点w的最短路径*/
public LinkedList path(int w){
LinkedList path = new LinkedList<>();
int p = from[w-1];
path.add(w);
while(p != -1){
path.addFirst(p);
p = from[p-1];
}
return path;
}
public void showPath(int w){
assert (0 < w && w <= graph.V());
LinkedList path = new LinkedList<>();
path = path(w);
for(int i : path){
System.out.print(i+"------>");
}
System.out.println();
}
/*返回边无权图source边到w边的最短路径长度*/
public int length(int w){
return order[w-1];
}
} 执行时间:进行广度优先搜索时,只有当顶点没有被访问时(visited[v] == false)才会将顶点加入到队列中,因此每个顶点只会被加入到队列中一次,将顶点加入到队列和从队列中删除的时间均为O(1),因此对队列进行的操作的总时间为O(V);扫描顶点的相邻顶点的操作只有在顶点从队列中删除时才会进行,因此扫描相邻顶点链表的操作也只会进行一次,用于扫描所有顶点的链表的总、时间为O(E+V)。因此广度优先搜索的运行时间是图G的邻接表大小的一个线性函数。
- 深度优先搜索
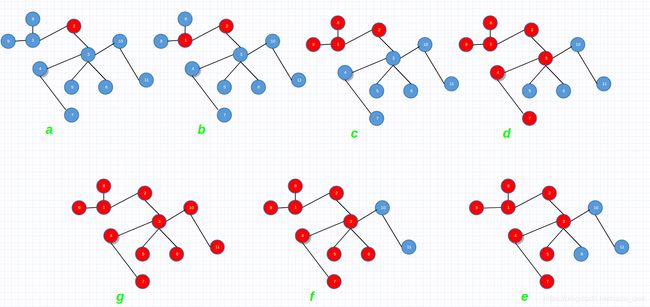
深度优先搜索另一种搜索图中顶点的方式,见名知意,这种搜索方式在图中尽可能深入。深度优先搜索总是对新近才发现的顶点v的相邻边进行探索,知道该顶点的所有相邻边都探索完为止。在顶点v的所有邻边探索完后,回溯到节点v的前驱顶点,继续探索前期顶点的邻边,如果前驱顶点的邻边也都探索完成就再次向上回溯直到所有可达到的顶点都被发现为止。如果还有未被发现的顶点,则将它作为新的起点重新开始探索过程直到图中的所有顶点都被发现,算法终止。下图是对图进行深度优先搜索的搜索过程。不同于广度优先搜索使用队列暂存顶点,深度优先搜索使用递归的方式进行搜索。
public class DFS {
/*记录节点是否被遍历*/
private boolean[] visited;
/*记录连通分量*/
private int ccount;
/*记录每个顶点属于那个图,if connected[i] == connected[j],顶点i和顶点j是连通的*/
private int[] connected;
/**
* 对图进行深度优先遍历
* @param graph
*/
public void traverseGraph(Graph graph){
assert (graph != null);
/*图的节点数目*/
int m = graph.V();
visited = new boolean[m];
connected = new int[m];
ccount = 0;
for (int i = 0; i < m; i++) {
visited[i] = false;
connected[i] = -1;
}
for (int i = 1; i <= m; i++) {
if(!visited[i-1]){
dfs(graph,i);
ccount++;
}
}
}
/*深度优先遍历的子过程*/
private void dfs(Graph graph, int v) {
visited[v-1] = true;
connected[v-1] = ccount;
Iterator integers = graph.adj(v);
integers.forEachRemaining(integer -> {
if(!visited[integer-1]) dfs(graph,integer);
});
}
public boolean isConnected(int v,int w){
return connected[v-1] == connected[w-1];
}
}
深度优先搜索解决两类问题:图中任意两个顶点是否连通的问题?图中的任意两个顶点之间是否存在一条路径?对于图中的顶点连通问题,也可以使用union-find来解决。