图论——基础知识1
图的基本概念
图(graph) G = ( V , E ) G=(V,E) G=(V,E)是一个二元组 ( V , E ) (V,E) (V,E)使得 E ⊆ [ V ] 2 E\sube [V]^2 E⊆[V]2,所以 E E E的元素是 V V V的2-元子集。默认是 V ∩ E = ∅ V\cap E = \empty V∩E=∅。
集合 V V V中的元素称为图 G G G的顶点(vertices)或节点(nodes),而集合 E E E的元素称为边(edges)。
具有顶点集 V V V的图称为 V V V上的图(a graph on V)。图 G G G的顶点集记为 V ( G ) V(G) V(G),边集记为 E ( G ) E(G) E(G)。
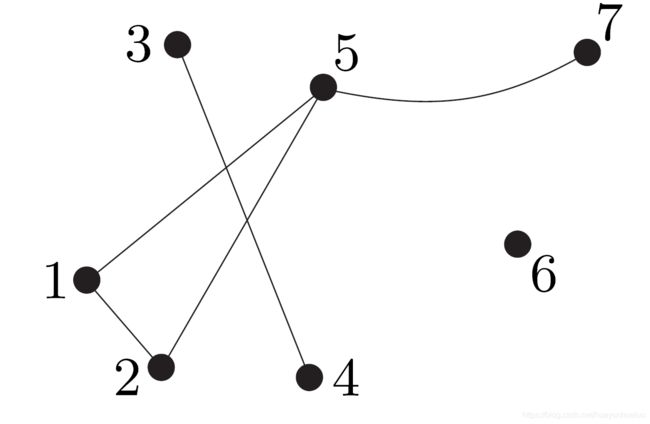
另外一个集合的记法:
图 H = ( W , F ) H=(W,F) H=(W,F)的顶点集 W W W仍记为 V ( H ) V(H) V(H)而不是 W ( H ) W(H) W(H)。通常并不把一个图和它的顶点集或边集严格区分开来
一个图的顶点个数称为它的阶(order),记为 ∣ G ∣ |G| ∣G∣,它的边数记为 ∣ ∣ G ∣ ∣ ||G|| ∣∣G∣∣。可以记为有限的、无限的、可数的等。
对于空图(empty graph)( ∅ , ∅ \empty,\empty ∅,∅),简记为 ∅ \empty ∅。阶为0或1的图称为平凡的(trivial)
给定顶点 v v v和边 e e e,如果 v ∈ e v\in e v∈e,则称 v v v与 e e e关联(incident),从而 e e e是在 v v v的边,关联同一条边的两个顶点称为这条边的端点(endvertices)或顶端(ends),而这条边连接(join)它的两个端点,边 { x , y } \{x,y\} {x,y}通常记为xy或yx。如果 x ∈ X x\in X x∈X且 y ∈ Y y\in Y y∈Y,则称边 x y xy xy为一条 X − Y X-Y X−Y边(X-Y edge)。
如果 x y xy xy是 G G G的一条边,则称两个顶点 x x x和 y y y是相邻的(adjacent)或邻点(neighbours),如果两条边 e ≠ f e\ne f e=f 有一个公共端点,则称 e e e和 f f f是相邻的(adjacent),若 G G G的所有顶点都是两两相邻的,则称 G G G是完全的(complete), n n n个顶点的完全图记为 K n K^n Kn, K 3 K^3 K3称为三角形。
互不相邻的顶点或边称为独立的(independent),如一个顶点集或边集中没有两个元素是相邻的,那么这个集合是独立的,也称为稳定集(stable set)
设 G = ( V , E ) G=(V,E) G=(V,E)和 G ′ = ( V ′ , E ′ ) G^{'}=(V^{'},E^{'}) G′=(V′,E′)是两个图,如果存在一个双射 ϕ : V → V ′ \phi: V\rightarrow V^{'} ϕ:V→V′使得所有 x , y ∈ V x,y\in V x,y∈V均有 x y ∈ E ⇔ ϕ ( x ) ϕ ( y ) ∈ E ′ xy\in E \Leftrightarrow \phi(x)\phi(y)\in E^{'} xy∈E⇔ϕ(x)ϕ(y)∈E′ ,则称 G G G和 G ′ G^{'} G′是同构的(isomorphic),记作 G ≃ G ′ G\simeq G^{'} G≃G′.这样的一个映射 ϕ \phi ϕ称为一个同构的。如果 G = G ′ G=G^{'} G=G′,则称它的一个自同构(automorphism)。
在同构意义下封闭的图族叫做图性质(graph property)。
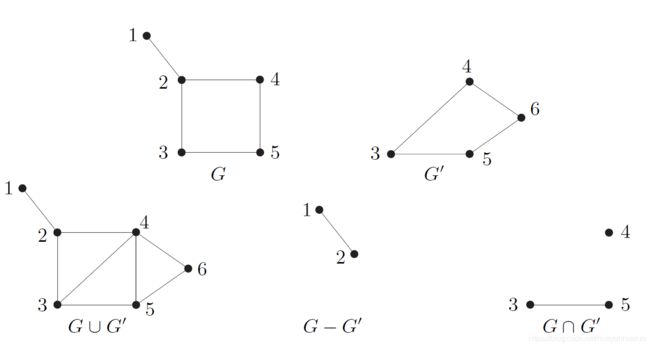
我们记为 G ∪ G ′ : = ( V ∪ V ′ , E ∪ E ′ ) G\cup G^{'}:=(V\cup V^{'},E\cup E^{'}) G∪G′:=(V∪V′,E∪E′)及 G ∩ G ′ : = ( V ∩ V ′ , E ∩ E ′ ) G\cap G^{'}:=(V\cap V^{'},E\cap E^{'}) G∩G′:=(V∩V′,E∩E′)。如果 G ∩ G ′ = ∅ G\cap G^{'}=\empty G∩G′=∅,则称为 G G G和 G ′ G^{'} G′是不相交的。如果 V ′ ⊆ V V^{'}\sube V V′⊆V且 E ′ ⊆ E E^{'}\sube E E′⊆E,则称 G ′ G^{'} G′是 G G G的子图(subgraph)并称为 G G G是 G ′ G^{'} G′的母图(supergraph)。
若 G ′ ⊆ G G^{'}\sube G G′⊆G且 G ′ G^{'} G′包含了 E E E中所有满足 x , y ∈ V ′ x,y\in V^{'} x,y∈V′的边xy,则称 G ′ G^{'} G′是 G G G的导出子图(induced subgraph),或称 V ′ V^{'} V′在图 G G G中导出(induces)或支撑(spans) G ′ G^{'} G′,并记为 G ′ = : G [ V ′ ] G^{'}=:G[V^{'}] G′=:G[V′]。如果 H H H是 G G G的子图(不必是导出子图),我们简记 G [ V ( H ) ] G[V(H)] G[V(H)]为 G [ H ] G[H] G[H]。最后如果 V ′ V^{'} V′支撑 G G G的所有顶点,即 V ′ = V V^{'}=V V′=V,则称 G ′ ⊆ G G^{'}\sube G G′⊆G是 G G G的一个支撑子图(spanning subgraph)
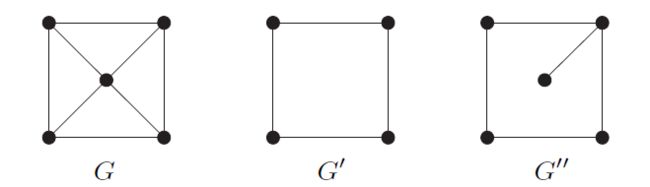
图G的子图 G ′ G^{'} G′和 G ′ ′ G^{''} G′′
设 U U U是G的任意顶点集合,我们把 G [ V \ U ] G[V \backslash U] G[V\U]简记为 G − U G-U G−U。换句话说 G − U G-U G−U是从 G G G中删除 U ∩ V U\cap V U∩V中所有顶点以及相关联的边而得到的图,如果 U = { v } U=\{v\} U={v}是个单点集,我们把 G − { v } G-\{v\} G−{v}简记为 G − v G-v G−v。而把 G − V ( G ′ ) G-V(G^{'}) G−V(G′)简单地记作 G − G ′ G-G^{'} G−G′。
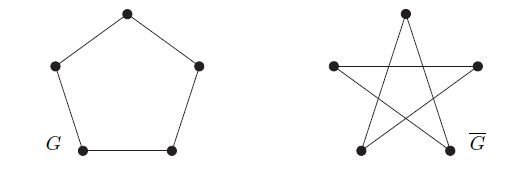
如果 G G G和 G ′ G^{'} G′是不交的,那么 G ⋅ G ′ G\cdot G^{'} G⋅G′表示在 G ⋃ G ′ G\bigcup G^{'} G⋃G′中连接G的所有顶点到 G ′ G^{'} G′的所有顶点而得到的图。图G的补图(complement) G ‾ \overline{G} G是V上边集 [ V ] 2 \ E [V]^2\backslash E [V]2\E的图。图G的线图(line graph) L ( G ) L(G) L(G)是E上的图。它们的顶点集是 E E E且使得 x , y ∈ E x,y\in E x,y∈E是相邻的当且仅当他们作为边在G中是相邻的。