DFS序与欧拉序的区别
DFS序与欧拉序的区别
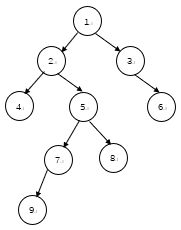
dfs序:是指将一棵树被dfs时所经过的节点顺序(不绕回原点)。
欧拉序:就是从根结点出发,按dfs的顺序在绕回原点所经过所有点的顺序。
作用
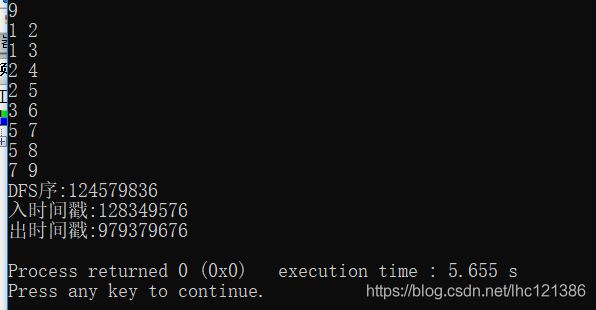
通过dfs序判断v节点的时间区间是否在u节点的时间区间内。
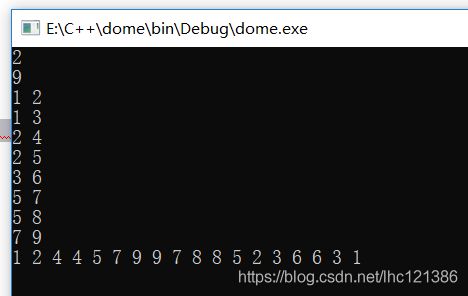
通过欧拉序求u和v的最近公共祖先。
用图说话
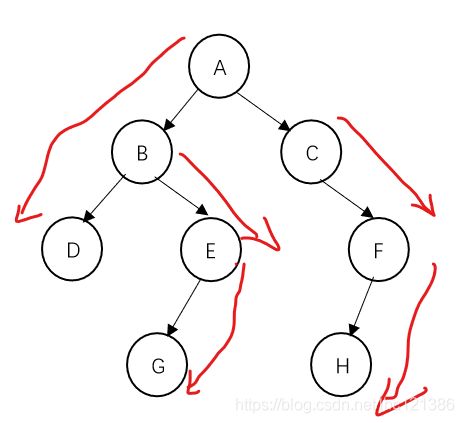
dfs序:A-B-D-E-G-C-F-H
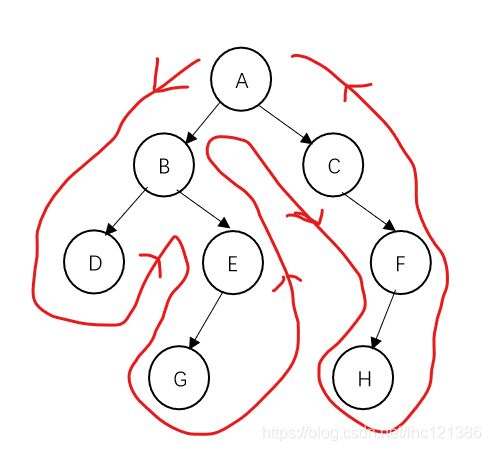
欧拉序:A-B-D-D-E-G-G-E-B-C-F-H-H-F-C-A
DFS序
DFS序核心代码
const int maxn = 1e5+5;
vector<int> g[maxn]; //存放节点
int s[maxn], e[maxn];//s[maxn]存放“入时间戳”,e[maxn]存放“出时间戳”;
int n,id,len;
int dfsxu[20000];//存放dfs序
void dfs(int u, int fa) {
s[u] = ++id;
dfsxu[++len]=u;
for(int i = 0; i < g[u].size(); ++i) {
int v = g[u][i];
if(v == fa) continue;
dfs(v, u);
}
e[u] = id;
}
DFS序完整代码
#include 通过dfs序判断v节点的时间区间是否在u节点的时间区间内
#include 欧拉序
核心代码:
vector<int> g[40010]; //存放节点
int oulaxu[80020]; //存放欧拉序在,在欧拉序中第一次出现为“入时间戳”,第二次出现为“出时间戳”。
int len;
void dfs(int u,int fa)
{
oulaxu[++len]=u;
int sz=g[u].size();
for(int i=0; i<sz; i++)
{
if(g[u][i]!=fa)
dfs(g[u][i],u);
}
oulaxu[++len]=u;
}
完整代码:
#include通过欧拉序求u和v的最近公共祖先
#include