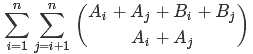【Atcoder agc001】E - BBQ Hard

E - BBQ Hard

---

Time limit : 2sec / Memory limit : 256MB

Score : 1400 points

Problem Statement

Snuke is having another barbeque party.

This time, he will make one serving of Skewer Meal.

He has a stock of N Skewer Meal Packs. The i-th Skewer Meal Pack contains one skewer, Ai pieces of beef and Bi pieces of green pepper. All skewers in these packs are different and distinguishable, while all pieces of beef and all pieces of green pepper are, respectively, indistinguishable.

To make a Skewer Meal, he chooses two of his Skewer Meal Packs, and takes out all of the contents from the chosen packs, that is, two skewers and some pieces of beef or green pepper. (Remaining Skewer Meal Packs will not be used.) Then, all those pieces of food are threaded onto both skewers, one by one, in any order.

(See the image in the Sample section for better understanding.)

In how many different ways can he make a Skewer Meal? Two ways of making a Skewer Meal is different if and only if the sets of the used skewers are different, or the orders of the pieces of food are different. Since this number can be extremely large, find it modulo 109+7.

Constraints

• 2≦N≦200,000
• 1≦Ai≦2000,1≦Bi≦2000

---

Input

The input is given from Standard Input in the following format:

N
A1 B1
A2 B2
:
AN BN

Output

Print the number of the different ways Snuke can make a serving of Skewer Meal, modulo 109+7.

---

Sample Input 1

3
1 1
1 1
2 1

Sample Output 1

26

The 26 ways of making a Skewer Meal are shown below. Gray bars represent skewers, each with a number denoting the Skewer Meal Set that contained the skewer. Brown and green rectangles represent pieces of beef and green pepper, respectively.

 

解析：

       一道很妙妙的题。

       首先有一个技巧，从（0,0）开始到（i，j）每次只能向上或向右，那么方案数即为C(i+j,i)或C(i+j,j)。

       如何理解？可以理解成因为从（0,0）到（i，j）的路线肯定有 i 个向右 j 个向上，只考虑向右，因为曼哈顿距离一定，所以一种方案对应一种向右的组合（稍微想一下就明白了）。

       回到这道题，它要求的是：

       

       于是对于每一个组我们可以建立起点（-a[i]，-b[i]）与终点（a[i]，b[i]），起点初始化为1，然后用刚才所说的方法DP以下即可。但要注意最后会算到自己到自己，直接减去C(a[i]*2+b[i]*2,a[i]*2)，并且还有重复计算的问题，因为这样算会算1与2,2与1，所以答案还要再除2（这里不能直接除要求逆元！）。

 

代码：

#include 
using namespace std;

const int Max=8010;
const int mod=1e9+7;
int n,m,k,ans;
int f[4010][4010],inv[Max],mul[Max],a[200010],b[200010];

inline int get_int()
{
	int x=0,f=1;
	char c;
	for(c=getchar();(!isdigit(c))&&(c!='-');c=getchar());
	if(c=='-') c=-1,c=getchar();
	for(;isdigit(c);c=getchar()) x=(x<<3)+(x<<1)+c-'0';
	return x*f;
}

inline int ksm(int a,int b)
{
	int ans=1;
	while(b)
	{
	  if(b&1) ans=(1ll*ans*a)%mod;
	  b>>=1;
	  a=(1ll*a*a)%mod;
	}
	return ans;
}

inline void pre()
{
	mul[0]=mul[1]=1;
	for(int i=2;i<=8000;i++) mul[i]=(1ll*mul[i-1]*i)%mod;
	inv[0]=inv[1]=1;
	for(int i=2;i<=8000;i++) inv[i]=ksm(mul[i],mod-2);
}

inline int C(int n,int m)
{
	if(n>=0 && m>=0 && n>=m) return (1ll*mul[n]*inv[m]%mod*inv[n-m]%mod)%mod;
	return 0;
}

int main()
{
	pre();
	n=get_int();
	for(int i=1;i<=n;i++) a[i]=get_int(),b[i]=get_int(),f[2001-a[i]][2001-b[i]]++;
	for(int i=1;i<=4001;i++)
	  for(int j=1;j<=4001;j++)
	    f[i][j]=(f[i][j]%mod+(f[i][j-1]+f[i-1][j])%mod)%mod;

	for(int i=1;i<=n;i++) ans=(ans+f[2001+a[i]][2001+b[i]])%mod;
	for(int i=1;i<=n;i++) ans=((ans-C((a[i]<<1)+(b[i]<<1),a[i]<<1))%mod+mod)%mod;
	ans=1ll*ans*(mod+1)/2%mod;
	cout<<(ans%mod+mod)%mod<<"\n";

	return 0;
}