bzoj 3210 //3210: 花神的浇花集会
bzoj 3210 //3210: 花神的浇花集会 //在线测评地址https://www.lydsy.com/JudgeOnline/problem.php?id=3210
更多题解,详见https://blog.csdn.net/mrcrack/article/details/90228694BZOJ刷题记录
2384 kb 276 ms C++/Edit 885 B
//3210: 花神的浇花集会
//在线测评地址https://www.lydsy.com/JudgeOnline/problem.php?id=3210
//题意没看太明白,样例也未模拟出。2019-10-30 20:28
//距离介绍,摘自https://blog.csdn.net/tianlan_sharon/article/details/50904641
//此文https://www.cnblogs.com/zwfymqz/p/8253530.html介绍得不错。2019-10-30 21:08
//此文https://blog.csdn.net/jzq233jzq/article/details/78725847证得不错
//此文https://blog.csdn.net/Riven__/article/details/79847143证得不错
//最小化曼哈顿距离,此文https://blog.csdn.net/yutianzuijin/article/details/95009923介绍得不错。
https://www.bbsmax.com/A/D854gqRxJE/
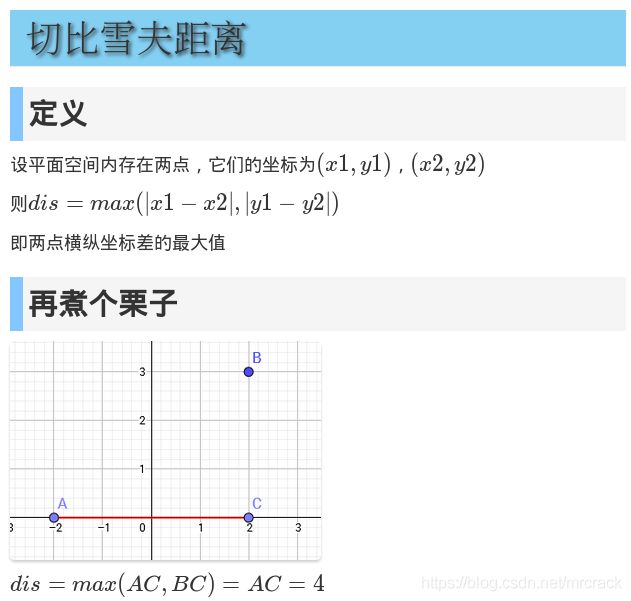
可以发现不合适度用的是切比雪夫距离。
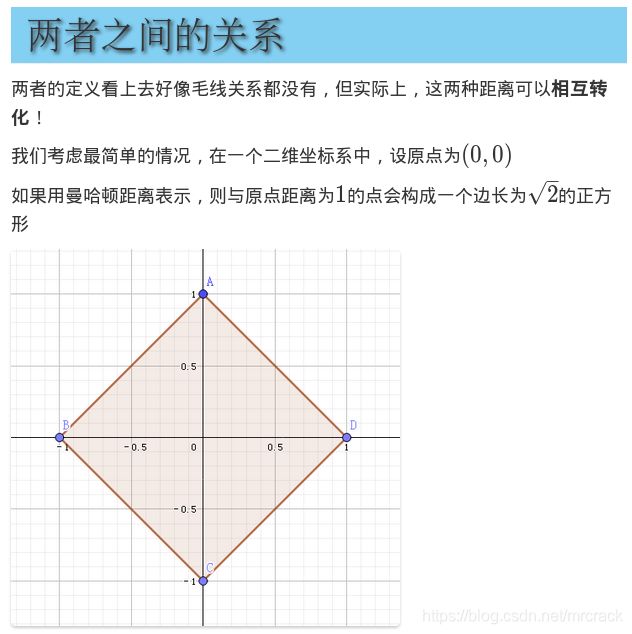
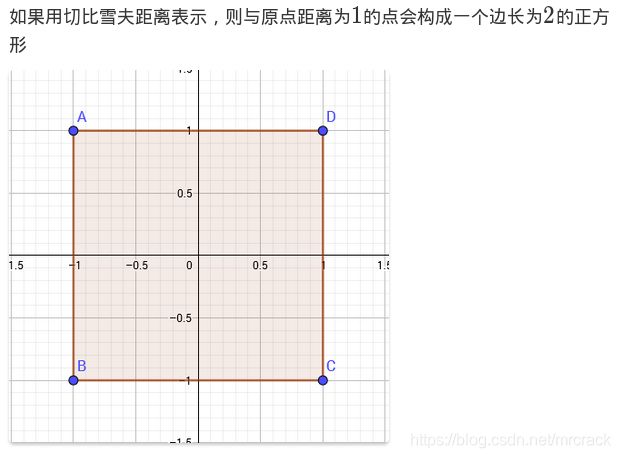
于是把(x,y)变成(x-y,x+y)转化为曼哈顿距离求解。
如果是曼哈顿距离就可以把横纵坐标分开来求。
可以用数学方法证明排序后中位数最优。
但有可能答案(x,y)不能用原来坐标为整数的点表示。
出现这种情况需要用(x,y-1),(x,y+1),(x-1,y),(x+1,y)几个点带进去取个min。
//此文https://www.bbsmax.com/A/D854gqRxJE/ 思路不错
/*
可以发现不合适度用的是切比雪夫距离。
于是把(x,y)变成(x-y,x+y)转化为曼哈顿距离求解。
如果是曼哈顿距离就可以把横纵坐标分开来求。
可以用数学方法证明排序后中位数最优。
但有可能答案(x,y)不能用原来坐标为整数的点表示。
出现这种情况需要用(x,y-1),(x,y+1),(x-1,y),(x+1,y)几个点带进去取个min。
*/
//此文http://hzwer.com/6835.html代码写得不错。
/*
LL t=0;//此处错写成LL t;样例输出为9,更正后,样例输出为3.
不初始化,不意味着t=0;上一行就是例子。
*/
//样例通过,提交AC.2019-10-31
#include
#include
#define LL long long
#define maxn 100100
using namespace std;
int a[maxn],b[maxn],x[maxn],y[maxn],n;
LL ans=1e20;
LL
int myabs(int x){
return x>=0?x:-x;
}
void solve(int x,int y){
int i;
LL t=0;//此处错写成LL t;样例输出为9,更正后,样例输出为3.
for(i=1;i<=n;i++)t+=max(myabs(a[i]-x),myabs(b[i]-y));//切比雪夫坐标
if(ans>t)ans=t;
}
int main(){
int i,j,kx,ky;
scanf("%d",&n);
for(i=1;i<=n;i++){
scanf("%d%d",&a[i],&b[i]);//切比雪夫坐标
x[i]=a[i]*0.5+b[i]*0.5,y[i]=a[i]*0.5-b[i]*0.5;//曼哈顿坐标
}
sort(x+1,x+1+n),sort(y+1,y+1+n);
kx=x[n/2+1]+y[n/2+1],ky=x[n/2+1]-y[n/2+1];//切比雪夫坐标
for(i=kx-1;i<=kx+1;i++)
for(j=ky-1;j<=ky+1;j++)
solve(i,j);
printf("%lld\n",ans);
return 0;
}
曼哈顿距离与切比雪夫距离的互化,此文https://www.cnblogs.com/SGCollin/p/9636955.html介绍得不错