用动态规划算法解决TSP问题
旅行商问题,即TSP问题(Traveling Salesman Problem)又译为旅行推销员问题、货郎担问题,是数学领域中著名问题之一。假设有一个旅行商人要拜访n个城市,他必须选择所要走的路径,路径的限制是每个城市只能拜访一次,而且最后要回到原来出发的城市。路径的选择目标是要求得的路径路程为所有路径之中的最小值。
环境:程序使用语言java,jdk版本1.8,程序中用到的jar包:poi-3.17
jar包下载地址:https://www.apache.org/dyn/closer.lua/poi/release/bin/poi-bin-3.17-20170915.tar.gz
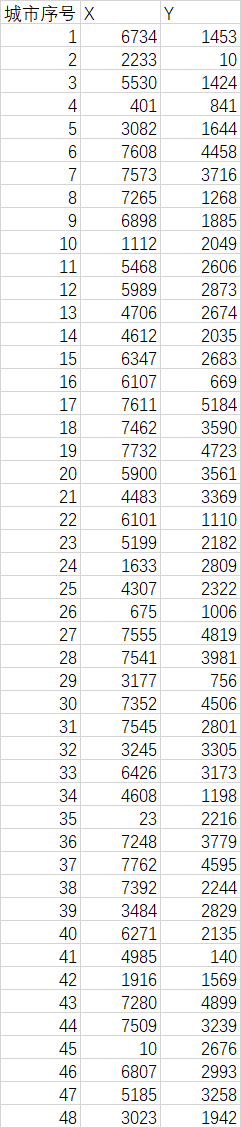
程序中使用的数据:下载地址:https://download.csdn.net/download/qq_35685675/10487174
项目导入:
3.实验主要源代码
City.java//城市类,结构体
package TSP;
publicclass city {
privateintname;
privatedoubleX;
privatedoubleY;
public city(intname, doublex, doubley) {
super();
this.name = name-1;
X = x;
Y = y;
}
publicint getName() {
returnname;
}
publicvoid setName(intname) {
this.name = name;
}
publicdouble getX() {
returnX;
}
publicvoid setX(doublex) {
X = x;
}
publicdouble getY() {
returnY;
}
publicvoid setY(doubley) {
Y = y;
}
@Override
public String toString() {
return"city [name=" + name + ",X=" + X + ", Y=" + Y + "]";
}
}
inputData.Java//导入数据类
package TSP;
import java.io.File;
import java.io.FileInputStream;
import java.io.FileNotFoundException;
import java.io.IOException;
import java.util.ArrayList;
import java.util.List;
import org.apache.poi.hssf.usermodel.HSSFRow;
import org.apache.poi.hssf.usermodel.HSSFSheet;
import org.apache.poi.hssf.usermodel.HSSFWorkbook;
publicclass inputData {
@SuppressWarnings("resource")
publicstatic List
List
try {
HSSFWorkbook wookbook = new HSSFWorkbook(new FileInputStream(file));
HSSFSheet sheet = wookbook.getSheet("Sheet1");
introws = sheet.getPhysicalNumberOfRows();
for(inti=1; i<rows; i++){
HSSFRow row = sheet.getRow(i);
if(row!=null){
city cy = new city(i, row.getCell(1).getNumericCellValue(), row.getCell(2).getNumericCellValue());
cityList.add(cy);
}
}
} catch (FileNotFoundException e) {
System.out.println("File not fount!");
} catch (IOException e) {
System.out.println("IO exception!");
}
returncityList;
}
}
DP.Java//核心代码
package TSP;
import java.io.File;
import java.util.List;
import java.util.Scanner;
public class DP {
//V集合表示已经旅行后的点的集合。
//n点经过集合V中所有点到达起始点的最短距离;1<<(n-1)代表一个二进制串,
//1代表该位置的城市在V集合例,反之不在。
static double INF = Double.MAX_VALUE;
static double[][] DT = null;
static double[][] DP = null;
// static int n = 0;
static void init(int n) {
File file = new File("E:\\Java\\arithmetic\\src\\resource\\att48.xls");
List
System.out.println("city [城市编号 城市X坐标 城市Y坐标]");
for(int i=0; i
}
DT = new double[n][n];
DP = new double[n][1<<(n-1)];
for(int i=0; i
else {
double dertX = cityList.get(i).getX()-cityList.get(j).getX();
double dertY = cityList.get(i).getY()-cityList.get(j).getY();
DT[i][j] = Math.sqrt(dertX*dertX + dertY*dertY);
DT[j][i] = DT[i][j];
}
}
}
// for(int i=0; i
// System.out.print(" ");
// }
// System.out.println();
// }
//V集合为空的情况,初始化第i点直接回到起点s的距离
for(int i=1; i
}
}
static void solve(int n) {
double minDt = INF;
double temp = 0;
for(int j=1; j<1<<(n-1); j++){//j的二进制表示V集合。
for(int i=1; i
minDt = INF;
for(int k=1; k
temp = DT[i][k] + DP[k][j-(1<<(k-1))];
if(temp < minDt) minDt = temp;
}
}
}
DP[i][j] = minDt;
}
}
minDt = INF;
for(int k=1; k
if(temp < minDt){
minDt = temp;
}
}
System.out.print("最短路径长:");
System.out.println(minDt);
}
@SuppressWarnings("resource")
public static void main(String[] args) {
// TODO Auto-generated method stub
System.out.println("----------------动态规划解决TSP问题----------------");
Scanner in = new Scanner(System.in);
while(true) {
System.out.println();
System.out.println("请输入城市数:");
int n = in.nextInt();
if(n>24) {
System.out.println("城市数过多,请使用其他算法!");
return;
}
init(n);
solve(n);
}
}
}
输入输出: