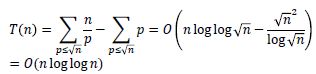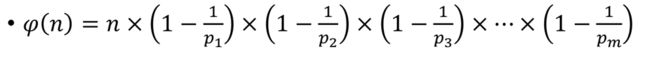【2019-总结】寒假数论专训总结
前言
没有时间了,上了5天的课已经颓废_(:з」∠)_,好不容易有一天的时间复习,明天就要考试了,祝自己好运
毕竟没有时间了,就【临时选一些自己认为比较重要的内容】,例题在PPT里面,时间关系没有节选出来,以后有时间再填这个巨坑qwq... ...
有一点很不好的就是...代码全是图片,有时间再手动码一遍吧...
大部分内容来自北大大二学长的讲课PPT
目录(寒假内容挺多的)
目录
前言
目录(寒假内容挺多的)
Day 1
一、模运算
二、素数/质数(Prime Number)
三、整数的唯一分解(标准分解)
四、最大公约数与最小公倍数
五、积性函数
六、筛法(Sieve Method)
Day 2
一、辗转相除法(欧几里得算法)
二、欧拉函数
三、欧拉定理
四、指数循环节(似乎也可以叫“降幂公式”)
五、费马小定理
六、二次探测定理
七、威尔逊定理
八、素数性质总结
Day 3
一、二元一次不定方程
二、扩展欧几里得算法
三、乘法逆元
Day 4
Day 1
一、模运算
数学基础知识——模运算(%)
• 有些时候答案非常大,题目会要求你输出答案对一个数取模的结
果
• (a+b)%c=(a%c+b%c)%c
• (a-b)%c=(a%c-b%c+c)%c
• (a*b)%c=(a%c)*(b%c)%c
• 也就是说如果你的算法只使用了加法、减法和乘法,你可以在所
有的中间步骤取模,这和只对答案取模是等效的。
• 第二天会给出具体证明。
二、素数/质数(Prime Number)
• 不含有除了1和自身以外的其他因子的数称为质数(素数)
• 2是最小的质数,也是唯一的偶质数
• 质数判别定理:若一个数n找不到小于等于根号n的非1因数,则这个
数是质数
• 素数定理(Gauss & Legendre)
• n充分大时,n以内的素数个数约等于n/logn个
——>这个对于做题时估算时间复杂度很有用
质朴的质数判断:
bool IsPrime(int x)
{
for(int i=2;i*i<=x;i++)
if(x%i==0)
return false;
return true;
}三、整数的唯一分解(标准分解)
• 一个大于1的整数一定可以唯一地写成若干质数的幂的积。![]() (后面会多次用到)
(后面会多次用到)
• 互质(Coprime):两个数没有公共的因数(除1以外),则这两个数互质。
• 将互质的两个数分别唯一分解后,两个积式中不会出现相同的质数。
下面的代码 i * i < = n也可以写成i < = sqrt (n)
void factorize(int x)
{
for(int i=2;i*i<=x;i++)
if(x%i==0)
{
p[++cnt]=i;
while(x%i==0)
x/=i,w[cnt]++;
}
if(x!=1)
p[++cnt]=x,w[cnt]=1;
}
/*
e.g.
156=2^2*3*13,sqrt(156)大于12,小于13
所以循环的时候i只枚举到了12,最后还需加上一个13
*/最后一个if语句很重要
四、最大公约数与最小公倍数
• 两个数的最大公因数记为gcd(x,y)或(x,y)
• 两个数的最小公倍数记为lcm(x,y)或[x,y]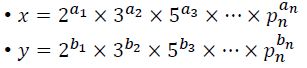
• 其中Pn充分大, ai,bi可以为0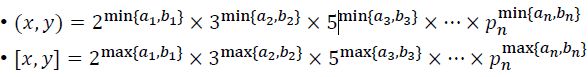
• 显然( x , y )[ x , y ] = xy (对多个数成立吗?)——>不成立啦qwq...
五、积性函数
• 积性函数对于所有互质的整数a和b有性质f ( a · b ) = f ( a ) · f ( b )
其实自己不是很理解积性函数
![]()
敲黑板!!!下面内容十分重要!
![]()
本人垃圾的小学奥数功底:约数个数口诀:指数加一再相乘
![]()
对于“因数和定理”,我个人的理解是:
对于第k种因数,可以为pk^0,pk^1,pk^2.....pk^ak,每种因数都是这样,最后根据【乘法原理】全部乘起来就是总和了
一道典例——后面有一道类似的题是1/(n!)=1/a+1/b
六、筛法(Sieve Method)
(一)•埃拉托斯特尼筛法(埃氏筛法):找到一个未被筛的(质)数 i,去掉 i 的所有倍数
• 筛法用于快速找出1~n的所有质数
void sieve(int n)
{
for(int i=2;i<=n;i++)
if(!vis[i])
{
prime[++cnt]=i;
for(int j=i+i;j<=n;j+=i)
vis[j]=1;
}
}这应该是本人用的最熟最喜欢的一种筛法了qwq
• 显然存在被重复筛去的数,例如18被2和3各筛了一次,所以不是线性的
(二)筛约数个数、约数和:
void sieve(int n)
{
for(int i=1;i<=n;i++)
for(int j=i;j<=n;j+=i)
d[j]++,s[j]+=i;
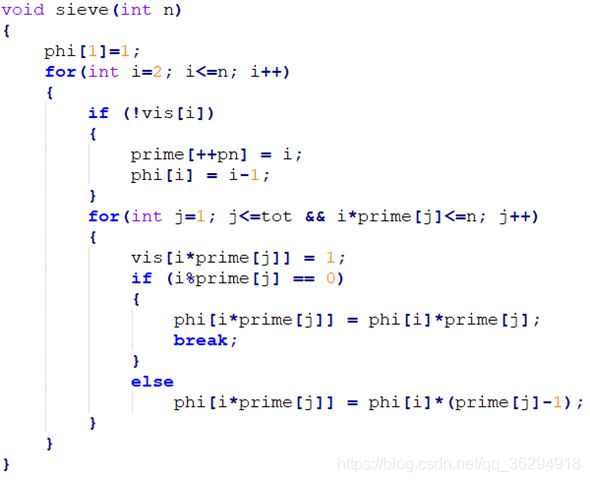
}(三)欧拉筛法:线性筛
![]()
一年前不理解,一年后的自己居然一看就看懂了qwq!
对每个合数a×b,它会被每个质因数都筛去一遍
但我们只要用最小的质因数筛去就好了
为此,我们需要记录下所产生的全部素数,代码如下
void sieve(int n)
{
for(int i=2;i<=n;i++)
{
if(!vis[i])
prime[++cnt]=i,vis[i]=1;
for(int j=1;j<=cnt&&i*prime[j]<=n;j++)
{
vis[i*prime[j]]=1;
if(i%prime[j]==0)
break;
}
}
}【核心】
if(i%prime[j]==0) break;如果i能整除primelist[k],
说明primelist[k]是i的因子,
所以primelist[k]也是i的任意倍数的因子。
所以primelist[k]也是i×primelist[x] (x>k)的因子。
考虑到primelist单增,对i×primelist[x],primelist[k]就是它的比primelist[x]更小的因子。
故不用考虑其后的质因子了。
(i×primelist[x]会被primelist[k]作为因子在i更大时被筛掉)
(四)欧拉筛法求约数个数d[n]
![]()
![]()
void sieve(int n)
{
d[1]=1;
for(int i=2;i<=n;i++)
{
if(!vis[i])
prime[++cnt]=i,vis[i]=1,num[i]=1,d[i]=2;
for(int j=1;j<=cnt&&i*prime[j]<=n;j++)
{
vis[i*prime[j]]=1;
if(i%prime[j]==0)
{
num[i*prime[j]]=num[i]+1;
d[i*prime[j]]=d[i]/(num[i]+1)*(num[i]+2);
break;
}
d[i*prime[j]]=d[i]*2;
num[i*prime[j]]=1;
}
}
}(五)欧拉筛法求约数和s[n]
![]()
![]()
void sieve(int n)
{
s[1]=1;
for(int i=2;i<=n;i++)
{
if(!vis[i])
prime[++cnt]=i,vis[i]=1,psum[i]=s[i]=i+1;
for(int j=1;j<=cnt&&i*prime[j]<=n;j++)
{
vis[i*prime[j]]=1;
if(i%prime[j]==0)
{
psum[i*prime[j]]=psum[i]*prime[j]+1;
s[i*prime[j]]=s[i]/psum[i]*psum[i*prime[j]];
break;
}
s[i*prime[j]]=s[i]*(prime[j]+1);
psum[i*prime[j]]=1+prime[j];
}
}
}Day 2
一、辗转相除法(欧几里得算法)
![]()
个人觉得度娘的证明更让我能理解=。=:
![]()
![]()
//辗转相除法算最大公因数
int gcd(int a,int b)
{
return b==0?a:gcd(b,a%b);
}
//(x,y)*[x,y]=x*y——>lcm(x,y)=x*y/gcd(x,y)
int lcm(int a,int b)
{
return a/gcd(a,b)*b;
}![]()
二、欧拉函数
重点!敲黑板! Leonhard Euler ,1707.4.15~1783.9.18
Leonhard Euler ,1707.4.15~1783.9.18
版本一:
版本二:
三、欧拉定理
再次敲黑板
四、指数循环节(似乎也可以叫“降幂公式”)
又一重点(黑板快敲烂了qwq...) 这个降幂公式蛮有用的
如其名字,就是用来降幂的,做题常用
![]()
五、费马小定理
六、二次探测定理
七、威尔逊定理
似乎有道例题专门考察这个定理...
八、素数性质总结
Day 3
一、二元一次不定方程
![]()
二、扩展欧几里得算法
自己的模板:d=gcd(a,b)
void exgcd(int a,int b)
{
if(!b)
{
x=1,y=0;
d=a;
return ;
}
else
{
exgcd(b,a%b);
int temp=x;
x=y;
y=temp-y*(a/b);
}
}三、乘法逆元
![]()
![]()
递推法求逆元:
![]()
#include
#include
#include
#include
#include
using namespace std;
void exgcd(int a,int b,int &d,int &x,int &y)
{
if(!b)
{
d = a;
x = 1;
y = 0;
}
else
{
exgcd(b, a%b, d, y, x);
y -= x*(a/b);
}
}
int inv(int a,int p)
{
int d, x, y;
exgcd(a, p, d, x, y);
return d == 1 ? (x+p)%p : -1;
}
int main()
{
int a,p;
scanf("%d %d",&a,&p);
printf("%d\n",inv(a,p));
}
Day 4
要考试了,先弄到这里... ...