图论（五）——以图的眼光看树&&编程求解图半径直径中心点

文章先叙述树、图离心率、半径和直径、中心等概念。之后会用c++一一实现~
欢迎关注我，后期会更新更多图算法哦23333

一、树的概念和性质

首先借助图来阐述几个概念：

• 树：不含圈的连通图。
• 森林：不含圈的图。
• 树叶：度为1的顶点。

\quad 考点1：如何求n阶不同构树的个数（按照树中存在的最长路进行枚举，n阶树中最长路为n-1，最短路为2，且最长路和最短路不同构的图仅一种）
\quad 考点2：如果电路是(n, m)图，则独立回路的个数为m-n+1。原因在与给G的生成树添上生成树外的一条边，就可以得到一独立回路，故回路数=m-(n-1)。
\quad 由定义可知，树和森林都是简单图，且都是偶图。树有许多特有的性质，接下来我们一一揭晓。

1、每棵非平凡树至少有两片树叶

\quad 首先我们要知道什么是平凡树呢？平凡树即平凡图，即只有一个顶点的图。且看证明：
\quad 设$P=v_1{v}_2\dots v_k$是非平凡树$T$中一条最长路，则$v_1$与$v_k$在$T$中的邻接点只能有一个，否则，要么推出$P$不是最长路，要么推出$T$中存在圈，这都是矛盾！即说明$v_1$与$v_2$是树叶。

2、图G是树当且仅当G中任意两点都被唯一的路连接

\quad 从必要性和充分性两点分别证明

• 必要性：设P1与P2是连接u与v的两条不同的路。则由这两条路的全部或部分将构成一个圈，这与G是树相矛盾。
• 充分性：因G的任意两点均由唯一路相连，所以G是连通的；若G中存在圈，则在圈中任取点u与v，可得到连接u与v的两条不同的路，与条件矛盾。

3、设T是（n，m）树，则m=n-1

\quad 常使用数学归纳法证明

4、具有k个分支的森林有n-k条边

\quad 设森林$G$包含k个分支$T_i(1\le i\le k)$，对于每个分支使用定理3可得：$m(T_i)=n_i-1$,故$m(G)={\sum }_{i=1}^{k}m(T_i)=n-k$。

5、每个n阶连通图的边数至少是n-1

6、任意树T的两个不邻接顶点之间添加一条边后，可以得到唯一圈

\quad 设$u$与$v$是树$T$的任意两个不邻接顶点，由定理2知：有唯一路$P$连接u与v.于是$P\cup \{uv\}$是一个圈。

7、树的度序列判定

\quad 设$S=｛d_1,d_2,\dots ,d_n｝$是n个正整数序列，它们满足：$d_1\geqq d_2\geqq \dots \geqq d_n,\sum d_i=2(n-1)$.则存在一颗树T，其度序列为S。

二、树的中心与形心

1、树的离心率及其半径、直径

\quad 设$v$是图$G=(V,E)$中一顶点，令$e(v)=max\{d(u,v)|u\in V\}$，则称$e(v)$为点$v$的离心率。（tips：说白了图中每个点都有一个对应的离心率，而这个离心率的大小就等于这个点到其他点最短距离的最大值）
\quad 半径：所有顶点中离心率的最小值，即$r(G)=min\{e(v)|v\in V\}$，则$r(G)$是图半径。
\quad 直径：所有顶点中离心率的最大值，即$d(G)=max\{e(v)|v\in V\}$，则$d(G)$是图半径。

2、图的中心

\quad 对于一个点$v$，$e(v)=r(G)$，则$v$是一个中心点，全体中心点的集合称为图的中心。

3、每棵树的中心由一个点或两个相邻点组成

\quad 树的叶子不可能是中心，我们每次删除叶子节点和其连接的那条边，直到剩下的节点不是叶子节点，那么这个点就是中心。这样的点只能是一个或者两个。
应用：确定社区医院的修建位置，就可以建模成求图的中心问题

4、树的形心

\quad 设u是树T的任意一个顶点，树T在顶点u的分支是指包含u作为一个叶点的极大子树，其分支数为顶点u的度数；树T在u点的分支中边的最大数目称为点u的权；树T中权值最小的点称为它的一个形心点。全体形心点的集合称为树T的形心。

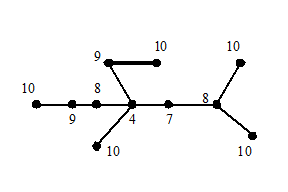
\quad 上图中顶点4就是树的形心。

三、算法实现

\quad 在求图的离心率、半径、直径和中心时，都离不开求图中任意两点间的最短距离。这里我们用$Floyed$完成，时间复杂度为$O(n^3)$。如果我们能确定这个图是树的话，那没两点之间仅有一条路，两点之间的那条路的距离即为最短路距离，这样的话用搜索算法能在$O(n^2)$时间复杂度下搞定。其实只要求出了图中每两个点间距离，要实现上述这些就很简单啦。代码如下：

//
// Created by 程勇 on 2019/3/12.
//

#include
using namespace std;

class center {
private:
    int v;  // 顶点数
    vector > g; // 存储图的边信息
    vector > dist; // 存储最短路信息
    const int maxNum = 0x3f3f3f3f;

public:
    center(int v)
    {
        this->v = v;
        g = vector >(v, vector(v, maxNum)); // 初始化边为无穷大
        for (int i = 0; i < v; ++i) {
            g[i][i] = 0;
        }
        dist = vector >(v, vector(v, 0));
    }

    void addEdge(int u, int v, int w);  // 添加边
    void floyed();
    vector > getDist() { return dist; } // 返回最短路信息矩阵
    int getEccentricity(int s);  // 得到s点对应的离心率
    int getRadius();  // 得到图半径
    int getDiameter();  // 得到图直径
    vector getGraphCenter(); // 获得图中心
};

void center::addEdge(int u, int v, int w) {
    g[u][v] = w;
    g[v][u] = w;  // 无向图
}

void center::floyed() {
    for (int i = 0; i < v; ++i) {
        for (int j = 0; j < v; ++j) {
            dist[i][j] = g[i][j];
        }
    }
    for (int k = 0; k < v; ++k) {
        for (int i = 0; i < v; ++i) {
            for (int j = 0; j < v; ++j) {
                if(dist[i][k]!=maxNum && dist[k][j]!=maxNum && dist[i][k]+dist[k][j] temp = dist[s];
    int res = 0;
    for (int i = 0; i < temp.size(); ++i) {
        if(res < temp[i]) res = temp[i];
    }
    return res;
}

int center::getRadius() {
    // 图半径为最小离心率
    int res = maxNum;
    for (int i = 0; i < v; ++i) {
        int temp = getEccentricity(i);
        if(temp < res) res = temp;
    }
    return res;
}

int center::getDiameter() {
    // 图直径为最大离心率
    int res = 0;
    for (int i = 0; i < v; ++i) {
        int temp = getEccentricity(i);
        if(temp > res) res = temp;
    }
    return res;
}

vector center::getGraphCenter() {
    /*
     * 对于图中一点v，若这点离心率等于图半径，则该点为图中心
     * 图中心可能不止一个，故用vector存储
     */
    vector res;
    int radius = getRadius();
    for (int i = 0; i < v; ++i) {
        if(getEccentricity(i)==radius)
            res.push_back(i);
    }
    return res;
}

\quad 以这个图为例，一共八个顶点，顶点编号为0-7，a点视为0，b点视为7，则：

int main()
{
    center G(8);
    G.addEdge(0, 1, 2);
    G.addEdge(0, 2, 8);
    G.addEdge(0, 3, 1);
    G.addEdge(1, 2, 6);
    G.addEdge(1, 4, 1);
    G.addEdge(2, 3, 7);
    G.addEdge(2, 4, 4);
    G.addEdge(2, 5, 2);
    G.addEdge(2, 6, 2);
    G.addEdge(3, 6, 9);
    G.addEdge(4, 5, 3);
    G.addEdge(4, 7, 9);
    G.addEdge(5, 6, 4);
    G.addEdge(5, 7, 6);
    G.addEdge(6, 7, 2);

    G.floyed();
    cout << "0点离心率:" << G.getEccentricity(0) << endl;  // 0点的离心率
    cout << "图半径：" << G.getRadius() << endl; // 打印图半径
    cout << "图直径：" << G.getDiameter() << endl; // 打印图直径
    vector center = G.getGraphCenter();  // 获得图中心
    cout << "图中心点集合：";
    for (int i = 0; i < center.size(); ++i) {
        cout << center[i] << " ";
    }
    return 0;
}

\quad 运行结果如下：