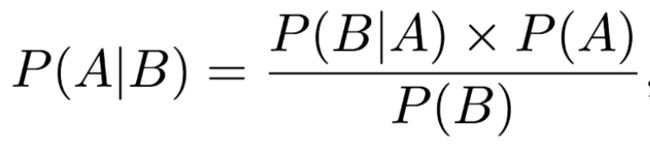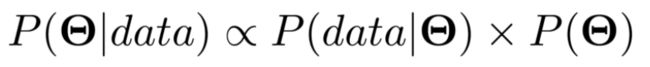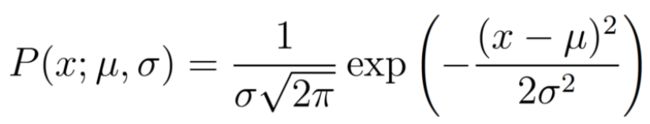概率论入门：贝叶斯推断

本文我们将介绍参数估计的另一个方法——贝叶斯推断。我同时将展示如何把这个方法看成最大似然的泛化版本，以及在什么情况下两个方法是等价的。

数学定义

在数学上，贝叶斯定理定义为：

其中，P(A|B)表示已知B事件发生的前提下A事件发生的概率（P(B|A)同理，只是A、B事件的角色互换了），P(A)和P(B)是A事件、B事件发生的边缘概率。

例子

数学定义经常太抽象，令人生畏，所以让我们使用一个例子来理解这个定义。我在本系列的第一篇文章使用过一个抽扑克牌的例子。一副牌有52张，26张红色，26张黑色。已知抽中的牌是红色，这张牌的数字是4的概率是多少？

我们用数学符号表示以上问题，P(4|红)。之前我们计算出这一概率是1/13（总共有26张红色的牌，其中有2张是4）但现在让我们使用贝叶斯定理来计算这个概率。

我们需要计算出贝叶斯定理右边的各项：

1. P(B|A) = P(红|4) = 1/2

2. P(A) = P(4) = 4/52 = 1/13

3. P(B) = P(红) = 1/2

将以上数字代入贝叶斯定理，我们得到1/13，和我们预期的答案一致。

贝叶斯定理如何允许我们纳入先验信念？

之前我提到过贝叶斯定理允许我们纳入先验信念，但是只看前文给出的等式，很难看出这是怎么办到的。所以让我们使用题图中的冰淇淋和天气的例子。

A表示我们看到冰淇淋的事件，B表示天气事件。接着我们也许会问已知天气类型的前提下，销售冰淇淋的概率是多少？在数学上这写作P(A=冰淇淋销售 | B=天气类型)，对应于贝叶斯定理等式的左侧。

等式右侧的P(A)被称为先验。在我们的例子中，这是P(A=冰淇淋销售)，即不考虑天气类型的情况下，销售冰淇淋的（边缘）概率。P(A)被称为先验是因为我们可能已经知道冰淇淋销售的边缘概率。例如，我可能查看过数据，100个潜在顾客中，有30人在某处的某家店实际购买了冰淇淋。所以，在我知道任何关于天气的信息之前，P(A=冰淇淋销售) = 30/300 = 0.3。这样，贝叶斯定理让我们纳入了先验知识。

注意：我之前提到了我可能通过一家店铺的数据获得先验知识，但是其实我完全可以编造完全主观的先验知识，不基于任何数据。有可能某人基于个人经历和特定的领域知识获得先验知识。先验知识的选择会影响最终的计算。我会在本文后面的部分详细讨论先验信念的强度如何影响结果。

贝叶斯推断

定义

现在我们知道贝叶斯定理是什么，以及它的用法，我们可以开始回答贝叶斯推断是什么这一问题。

首先，（在统计学上）推断是推理数据的种群分布或概率分布的性质的过程。上一篇最大似然的文章其实就包含了这一过程。我们基于观察到的一组数据点决定均值的最大似然估计。

因此贝叶斯推断不过是使用贝叶斯定理推理数据的种群分布或概率分布的性质的过程。

将贝叶斯定理应用于分布

到目前为止，所有的例子中，贝叶斯定理的每一项的值都是单个数字。这意味着我们得到的答案也将是单个数字。然而，有时候单个数字可能不怎么合适。

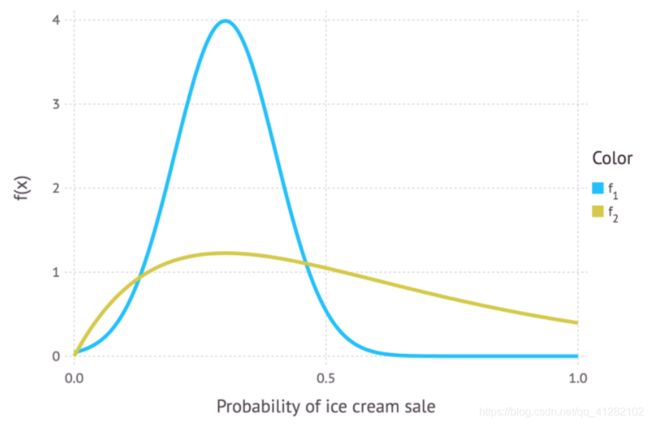
在前文的冰淇淋的例子中，我们看到销售冰淇淋的先验概率是0.3。然而，如果0.3只是我的最佳猜测，我并不是非常确定，会怎么样？概率也可能是0.25或0.4。在这一情形下，用一个分布来表示我们的先验信念可能更加合适（见下图）。这一分布被称为先验分布。

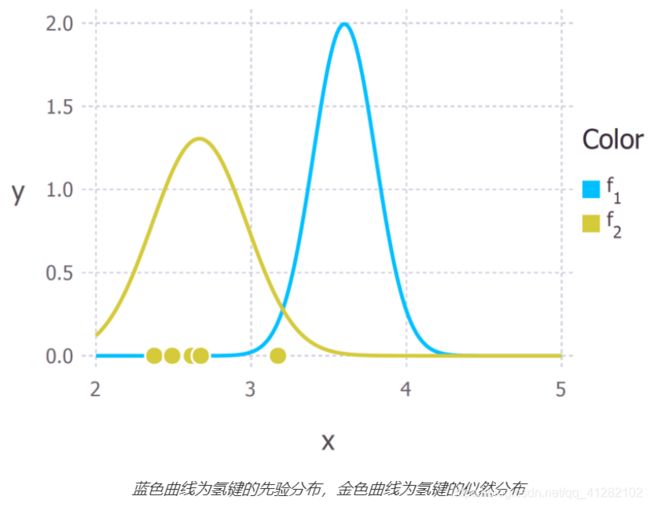
上图为表示任意一天冰淇淋销售的两个分布。蓝色曲线和金色曲线的峰值均位于0.3附近，如前所述，这是我们对冰淇淋销售的先验概率的最佳猜测。而f(x)在其他处的值并不为零，表明我们并不是完全确信0.3是冰淇淋销售的真实值。蓝色曲线显示它可能是0到0.5之间的任何值，而金色曲线显示它可能是0和1之间的任何值。相比蓝色曲线，金色曲线更为舒展，峰值更低，这意味着金色曲线表达的先验概率“不那么确定”。

基于类似的方法，我们可以用分布表示贝叶斯定理中的其他项。当我们处理模型的时候，大多数情况下我们都需要使用分布。

贝叶斯定理的模型形式

前文介绍贝叶斯定理的定义时，我使用A、B表示事件。但关于贝叶斯定理的模型形式的文献往往使用不同的符号。

我们通常使用Θ而不是A。Θ表示一组参数。所以如果我们尝试估计高斯分布的参数值，那么Θ表示均值μ和标准差σ（在数学上写作Θ = {μ, σ}）。

我们通常使用data或者y = {y1, y2, ..., yn}，而不是B。这代表数据，也就是我们的观测集合。我会在等式中显式地使用data，希望这能让等式看起来不那么晦涩。

因此，贝叶斯定理的模型形式写作：

P(Θ)为先验分布，表示我们关于参数的真值的信念，就像我们之前用分布表示我们关于冰淇淋销售的概率的信念。

等式左边的P(Θ|data)称为后验分布。它表示基于已经观测到的数据计算出等式右边的各项之后我们对参数的信念。

其实我们之间已经接触过P(data|Θ)。如果你读完了我前一篇关于最大似然的文章，那么你会记得我们提到过L(data; μ, σ) 是（高斯分布的）似然分布。好，P(data|Θ) 正是这个，它是改头换面的似然分布。有时它写作ℒ(Θ; data)，都是一回事。有时它被称为证据。

因此，我们可以通过证据更新我们的先验信念来计算我们的参数的后验分布。

这给了我们充足的信息来讨论使用贝叶斯推断来推断参数的一个例子。但是首先……

为什么我完全忽视了P(data)？

除了数据的边缘概率之外，P(data)并没有什么特别的名字。记住，我们关心的是参数值，而P(data)并没有提到参数。事实上，P(data)甚至不是一个分布。它只是一个数字。我们已经观测到了数据，因此我们计算出P(data)。一般而言，结果我们发现计算P(data)会非常困难，存在太多方法计算它的方法。Prasoon Goyal的这篇博客解释了其中一些方法。

P(data)之所以重要，是因为它得出的数字是一个归一化常量。概率分布的一个必要条件是一个事件的所有可能性的概率之和为1（例如，投掷一枚6面骰得到1、2、3、4、5、6点的全概率等于1）。归一化常量通过确保分布之和（其实我应该说积分，因为通常我们碰到的是连续分布，不过目前这么说太过于卖弄学问了）等于1来确保所得的后验分布是真实概率分布。

在某些情况下，我们并不关心分布的这一性质。我们只关心分布的峰值何时出现，而不在乎分布是否归一化。在这一情况下，很多人把贝叶斯定理的模型形式写作：

其中∝表示“成比例”。这显式地表明了真实后验分布不等于右边的式子，因为我们没有考虑归一化常量P(data)。

贝叶斯推断的例子

下面我们将继续讨论一个用贝叶斯推断来处理会比较顺手的例子。我们将使用的例子是求氢键的长度。你并不需要知道氢键是什么。我只是拿它做一个例子，这是在我读博的时候帮助朋友解决的一个问题（当时我们在生化部门）。

我加上了这张图片是因为我觉得它看起来挺不错的，有助于打断密集的文本，某种意义上也和我们要讨论的例子相关。别担心，你不需要理解这张图片以理解我们的贝叶斯推断过程。万一你好奇这张图片从哪里来，那我告诉你这张图片是我用Inkscape自己做的。

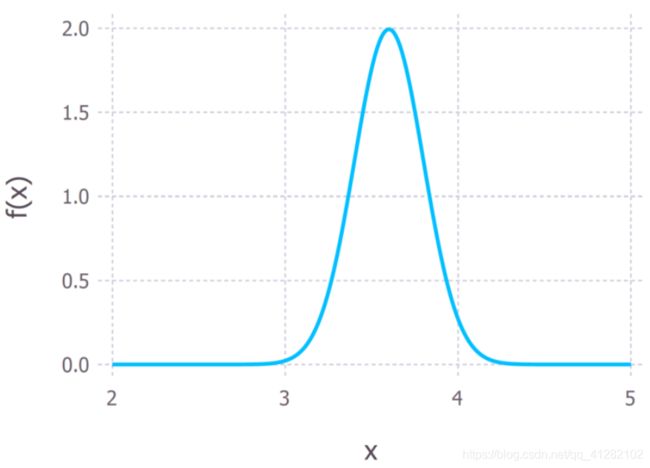
让我们假定氢键的长度在3.2Å到4.0Å之间（我google了一下得到了这个结果，埃，Å，是一个长度单位，1Å等于0.1纳米，所以我们谈论的是一个非常小的尺度）。这一信息将构成我们的先验。用概率分布的术语来说，我将其形式化地表示为均值μ = 3.6Å、标准差σ = 0.2Å的高斯分布（见下图）。

                                                                                                氢键长度的先验概率

现在我们提供一些数据（准确的说，是基于均值为3Å、标准差为0.4Å的高斯分布随机生成的5个数据点。在现实世界场景中，这些数据将来自科学试验的结果），这些数据给出了氢键的长度（下图中金色的点）。我们可以使用最大似然得到数据的似然分布，正如我们在前一篇文章中所做的那样。假定数据是使用可以用高斯分布描述的过程生成的，我们得到下图中金色曲线表示的似然分布。注意最大似然估计得到的5个数据点的均值低于3（约为2.8Å）。

现在我们有两个高斯分布，蓝色代表先验，金色代表似然。我们并不在乎归一化常量，因此我们具备了计算未归一的后验分布的一切信息。回顾一下，表示高斯分布的概率分布的等式为：

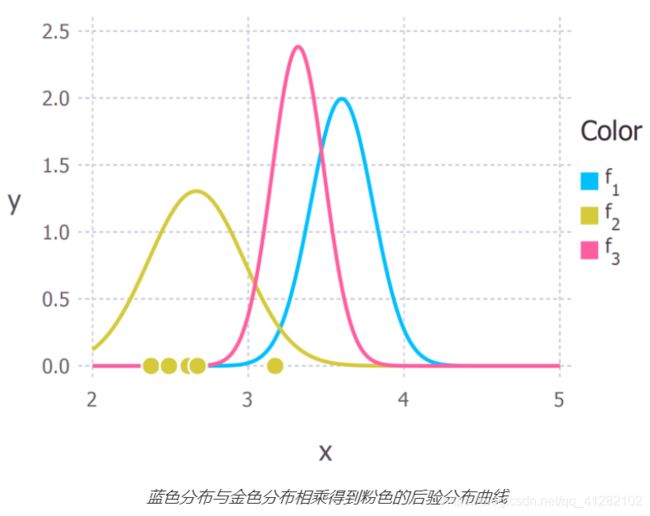
所以我们将取两个分布的乘积。我不会在这里详细列出数学上的运算过程，因为这会很凌乱。如果你对数学感兴趣，你可以参考这篇文档的前2页。下图中的粉色曲线表示所得的后验分布。

现在我们得到了氢键长度的后验分布，我们可以从中提取数据。例如，我们可以使用分布的期望值来估计距离。或者我们可以计算方差以量化我们结论的不确定性。从后验分布中，我们最常计算的是众数。众数经常被用来估计感兴趣的参数的真值，我们称其为最大后验概率估计（Maximum a posteriori probability estimate），简称MAP估计。在我们的例子中，后验分布同时也是高斯分布，因此均值等于众数（也等于中位数），氢键距离的MAP估计位于分布的峰顶处（约为3.2Å）。

结语

怎么总是高斯分布？

你会注意到，我们所有关于分布的例子中都使用了高斯分布。主要的一个原因是这大大简化了数学。但是在贝叶斯推断的例子中 ，我们得计算两个分布的乘积。我说过这很凌乱，所以我没有详细列出数学计算过程。但是即便我自己没有进行这些数学计算，我早就知道后验分布会是高斯分布。因为高斯分布具有一个特别的性质，使得高斯分布易于处理。高斯分布和自身的高斯似然函数是共轭的。这意味着，如果我将一个高斯先验分布乘以一个高斯似然函数，我将得到一个高斯后验函数。后验与先验来自同一分布家族（它们都是高斯分布）意味着它们是共轭分布。在这个例子中，先验分布是一个共轭先验。

在很多推断的场景中，我们选择使所得分布共轭的似然和先验，因为这简化了数学。数据科学中的一个例子是隐含狄利克雷分布（LDA），这是一种在多个文档（语料库）中搜寻主题的无监督学习算法。Edwin Chen的博客上有一篇非常出色的LDA的介绍。

在某些情形下，我们不能简单地选择简化后验分布计算过程的先验或似然。有时似然和/或先验分布看起来会很吓人，手工计算后验不容易，甚至不可能。在这些情形下，我们可以使用不同的方法计算后验分布。最常用的方法之一是马尔可夫链蒙特卡罗法。Ben Shaver写过一篇很棒的文章无需数学公式就让你明白什么是马尔可夫链蒙特卡罗法，以非常平易近人的方式解释了这一技术。

我们获得新数据时会发生什么？

贝叶斯推断的一个巨大优势就是你不需要大量数据就可以使用它。一个观察足够更新先验。事实上，贝叶斯框架允许你随着数据的流入迭代地实时更新你的信念。你具备对某事的先验信念（例如，参数的值），接着你收到了一些数据。你可以像我们之前做的那样通过计算后验概率来更新你的信念。之后，我们收到更多的数据。因此我们的后验这时变成了先验。我们可以通过基于新数据得到的似然更新我们的新先验，再次得到一个新后验。无限循环往复，不断更新你的信念。

卡尔曼滤波（及其变体）是一个很好的例子。它用于许多场景，但在数据科学中，最引人注目的应用是无人驾驶汽车。我读博期间在蛋白质结晶学中使用了卡尔曼滤波的一个变体，无轨迹卡尔曼滤波（Unscented Kalman filter），并给实现这一变体的开源软件包贡献了代码。你可以参考Tim Babb的博客How a Kalman filter works, in pictures（卡尔曼滤波工作机制图示），一个很好的卡尔曼滤波的可视化描述。

使用先验作为正则化项

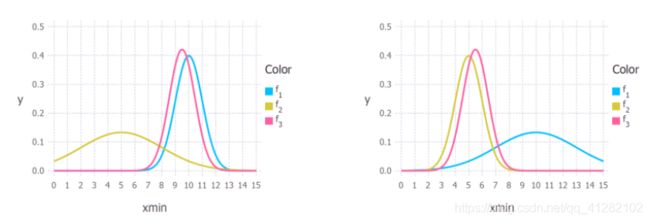
前文的氢键长度例子中我们生成的数据表明2.8Å是最佳估计。然而，如果我们仅仅根据数据进行估计，我们可能会有过拟合的风险。如果数据收集过程出了差错，这个问题会很严重。在贝叶斯框架中，我们可以使用先验来解决这个问题。在我们的例子中，一个3.6Å的高斯先验得到了一个后验分布，该分布给出的氢键长度的MAP估计为3.2Å。这展示了我们的先验在估计参数值时可以作为正则化项。

先验和似然给出的权重取决于两个分布的相对不确定性。在下图中我们可以从图像上看到这一点。颜色和前文一样，蓝色代表先验分布，金色代表似然，粉色代表后验。左图中，你可以看到，先验（蓝色）远不如似然（金色）那样舒展。因此相比似然，后验更接近先验。右图的情况恰恰相反。

因此，如果我们希望增加一个参数的正则化，我们可以相对于似然收紧先验分布。

Michael Green写过一篇The truth about Bayesian priors and overfitting（贝叶斯先验和过拟合的真相），详细讨论了这一问题，并给出了如何设置先验的建议。

什么时候MAP估计等于最大似然估计？

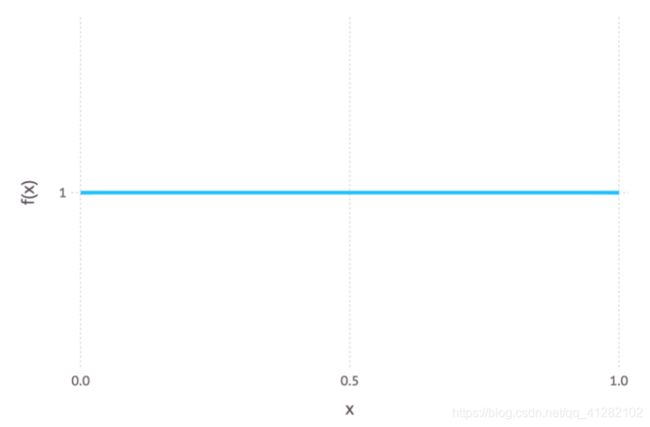
当先验分布是均匀分布时，MAP估计等于先验分布。下面是一个均匀分布的例子。

我们看到，均匀分布赋予x轴上的每个值相同的权重（它是一条水平线）。直觉上它表示缺乏哪个值可能性更大的任何先验知识。在这一情形下，所有的权重归于似然函数，所以当我们将先验与似然相乘的时候，所得的后验精确地重现了似然。因此，我们可以把最大似然方法看成MAP的一个特例。