图
一、图的基本概念
1.什么是图?
有向图与无向图;
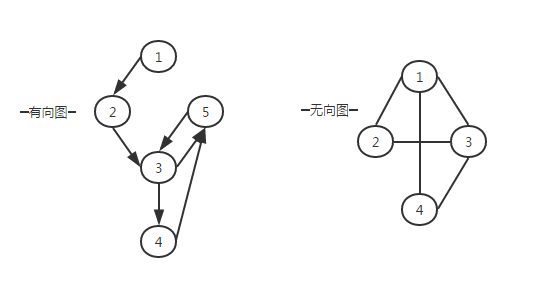
顶点
弧:弧尾和弧头
度:出度和入度
顶点
边
邻接点
连通图
完全图:边数=n(n-1)/2
生成树:边数=n-1
2、图的存储方式
对于无向图:存储顶点及边
对于有向图:存储顶点及弧
弧尾———-权值———狐尾
邻接矩阵
一个n顶点图G=(V,E)的邻接矩阵是一个n×n的矩阵,其中每个元素是0或者1.
无向图中元素定义:A(i,j) = 1 (如果(i,j)∈E或(j,i)∈E) 或者 A(i,j)= 0
无向图的邻接矩阵是对称的。
有向图元素定义:A(i,j)= 1 (如果(i,j)∈E)或者 A(i,j)= 0
图的连接矩阵
typedef char VertexType; //结点类型
typedef int EdgeType; //边上的权值类型
#define MAXVEX 100 //最大顶点数
#define INFINITY 65535 //用65535来代替无穷大
typedef struct
{
VertexType vexs[MAXVEX]; //顶点表
EdgeType arc[MAXVEX][MAXVEX]; //邻接矩阵,可看作表
int numVertexes,numEdges; //图中当前的顶点数和边数
}MGraph;
无向图的连接矩阵
void CreateMGraph(MGraph *G)
{
int row,col,value;
std::cout<<"请输入顶点数和边数"<<std::endl;
std::cin>>G->numVertexes>>G->numEdges;
std::cout<<"读入顶点信息,建立顶点表"<<std::endl;
for(int i=0;i<G->numVertexes;i++) //读入顶点信息,建立顶点表
{
std::cin>>G->vexs[i];
}
//邻接矩阵初始化
for(int i=0;i<G->numVertexes;i++)
{
for(int j=0;j<G->numVertexes;j++)
{
G->arc[i][j]=INFINITY;
}
}
for(int k=0;k<G->numEdges;k++)
{
std::cout<<"输入边(Vi,Vj)上的下标i,下标j和权w:"<<std::endl;
std::cin>>row>>col>>value;
G->arc[row][col]=value;
G->arc[col][row]=G->arc[row][col]; //因为是无向图,所以矩阵对称
}
}
邻接表
创建代码
void CreateALGraph(GraphAdjList *G)
{
int row,col;
EdgeNode *e;
std::cout<<"输入顶点数和边数"<<std::endl;
std::cin>>G->numVertexes>>G->numEdges;
//读入顶点信息,建立顶点表
for(int i=0;i<G->numVertexes;i++)
{
std::cin>>G->adjList[i].data; //输入顶点信息
G->adjList[i].firstedge=nullptr; //将边表置为空表
}
//建立边表
for(int i=0;i<G->numEdges;i++)
{
std::cout<<"输入边(Vi,Vj)上的顶点序号:"<<std::endl;
std::cin>>row>>col;
e=(EdgeNode *)malloc(sizeof (EdgeNode));
e->adjvex=col;
e->next=G->adjList[row].firstedge;
G->adjList[row].firstedge=e;
e=(EdgeNode *)malloc(sizeof (EdgeNode));
e->adjvex=row;
e->next=G->adjList[col].firstedge;
G->adjList[col].firstedge=e;
}
}
深度优先搜索
深度优先搜索有点类似二叉搜索树中的前序遍历
void Graph::depthTraverse(int nodeIndex)
{
int value = 0;
cout << m_pNodeArray[nodeIndex].m_cData << " ";
m_pNodeArray[nodeIndex].m_bIsVisited = true;
for (int i = 0; i < m_iCapacity; i++) {
getValueFromMatri(nodeIndex, i, value);
if (value == 1) {
if (m_pNodeArray[i].m_bIsVisited == true)
else {
depthTraverse(i);
}
}
else {
continue;
}
}
}`
广度优先搜索
从一个顶点开始,搜索所有可以到达顶点的方法叫做广度优先搜索。
Prim算法更适合求稠密图的最小生成树【稠密图的无向网更适合使用邻接矩阵形式存储】
Kruskal算法更适合求稀疏图的最小生成树【稀疏图的无向网更适合使用邻接表形式存储】
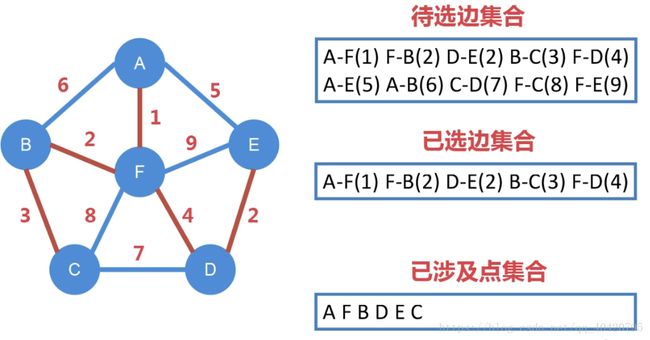
克鲁斯卡尔算法
算法思想:
- 将所有边放入待选边集合中;
- 取出当前待选边集合中权值最小的边放入已选边集合中,将边所连接的两个顶点放入已涉及点集合中
3.重复步骤2,如果已涉及的点的集合中的点不处于同一棵树中,则继续重复步骤2,直到已涉及的点的集合包含所有的点且所有点都在同一棵树中,最小生成树也就随之产生了; - 克鲁斯卡尔算法适用于边数较少的稀疏图,算法复杂度为o(n^2);
普利姆算法算法基本思想
(1)构造一个只有原连通带权图顶点的新图,即没有边只有顶点(每个顶点都是一个连通分量);
(2)从顶点中选择一个顶点作为起始连通分量;
(3)选择与此连通分量连接的边中权值最小的边,加入连接的顶点且将此边加入到新图中,将此边舍去;
(4)重复步骤(3),直到所有顶点同时在一个连通分量上。
![]()
上图左边为图的性质,右边为对应的邻接矩阵。
选择A作为出发顶点,步骤如下:
{A}->G
{A,G}->B
{A,G,B}->E
{A,G,B,E}->F
{A,G,B,E,F}->D
{A,G,B,E,F,D}->C
{A,G,B,E,F,D,C}
4两种算法的比较 (Comparing Two Algorithms)
方式:
Kruskal通过边来构造最小生成树;
Prim通过顶点来构造最小生成树;
适用范围:
Kruskal对边稀疏与边稠密都适用;
Prim仅对边稠密适用;
复杂度(n个顶点,e条边,插入删除等使用小根堆O(log2e)):

