The Majestic Brown Tree Snake

There is an undirected tree of $n$ vertices, connected by $n-1$ bidirectional edges. There is also a snake stuck inside of this tree. Its head is at vertex $a$ and its tail is at vertex $b$. The snake’s body occupies all vertices on the unique simple path between $a$ and $b$.

The snake wants to know if it can reverse itself — that is, to move its head to where its tail started, and its tail to where its head started. Unfortunately, the snake’s movements are restricted to the tree’s structure.

In an operation, the snake can move its head to an adjacent vertex not currently occupied by the snake. When it does this, the tail moves one vertex closer to the head, so that the length of the snake remains unchanged. Similarly, the snake can also move its tail to an adjacent vertex not currently occupied by the snake. When it does this, the head moves one unit closer to the tail.

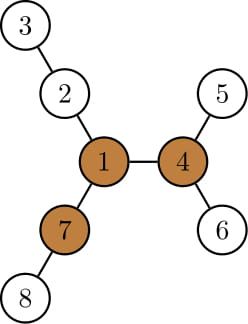
Let’s denote a snake position by $(h,t)$, where h is the index of the vertex with the snake’s head, $t$ is the index of the vertex with the snake’s tail. This snake can reverse itself with the movements $(4,7)\to (5,1)\to (4,2)\to (1,3)\to (7,2)\to (8,1)\to (7,4)$.
Determine if it is possible to reverse the snake with some sequence of operations.

Input
The first line contains a single integer $t$ $(1\le t\le 100)$ — the number of test cases. The next lines contain descriptions of test cases.

The first line of each test case contains three integers $n,a,b$ $(2\le n\le 10^5,1\le a,b\le n,a\ne b)$.

Each of the next $n-1$ lines contains two integers $u_i,v_i$ $(1\le u_i,v_i\le n,u_i\ne v_i)$, indicating an edge between vertices $u_i$ and $v_i$. It is guaranteed that the given edges form a tree.

It is guaranteed that the sum of $n$ across all test cases does not exceed $10^5$.

Output
For each test case, output “YES” if it is possible for the snake to reverse itself, or “NO” otherwise.

Example

input
4
8 4 7
1 2
2 3
1 4
4 5
4 6
1 7
7 8
4 3 2
4 3
1 2
2 3
9 3 5
1 2
2 3
3 4
1 5
5 6
6 7
1 8
8 9
16 15 12
1 2
2 3
1 4
4 5
5 6
6 7
4 8
8 9
8 10
10 11
11 12
11 13
13 14
10 15
15 16
output
YES
NO
NO
YES

Note
The first test case is pictured above.

In the second test case, the tree is a path. We can show that the snake cannot reverse itself.

In the third test case, we can show that the snake cannot reverse itself.

In the fourth test case, an example solution is:

$$\begin{gathered} (15,12)\to (16,11)\to (15,13)\to (10,14)\to (8,13)\to (4,11)\to (1,10) \\ \to (2,8)\to (3,4)\to (2,5)\to (1,6)\to (4,7)\to (8,6)\to (10,5) \\ \to (11,4)\to (13,8)\to (14,10)\to (13,15)\to (11,16)\to (12,15) \end{gathered}$$.

定义关键点：对于某个点，如果从该点出发的三条不相交的路径长度均大于蛇的长度$len$，则称该点为关键点。

这里有一个结论：蛇的一端能够到达关键点，是这条蛇能够掉头的充要条件。
结论的充分性是显然的，必要性可以通过假设蛇不能到关键点，然后用反证法证明。

关键节点可以用一次树形$dp$和一次换根$dp$ $O(n)$求出。

如果不存在关键点，那么蛇一定不能掉头，这种情况直接输出"NO"即可。

如果存在关键点，那么接下来就是判断蛇能不能到达关键点。

先说结论：如果存在关键点，那么蛇能到达关键点的充要条件是蛇的头和尾能到达的点集有重合。

• 证明充分性：
  因为蛇的头和尾能到达的点集有重合，所以显然蛇能够拐进任意一个岔路，因此蛇的端点能够到达任意一个点，也就能到达关键点。

• 证明必要性：
  因为蛇能到达关键点，所以蛇能够掉头，因此蛇的头和尾能到达的点集有重合。

为了让蛇头和尾能到达的点集有重合，采用贪心策略每次让蛇头和蛇尾走到最深的地方。
最多进行$O(\sqrt{n})$次移动就可以得出结论。
证明如下：

最坏情况如图所示，假设蛇的长度为$l$(边数)，则点的数量$n=l+1+\frac{(l+1)l}{2}=\frac{(l+1)(l+2)}{2}$，因此蛇的长度$l$为$O(\sqrt{n})$级别的。而移动次数为$l$，因此最多进行$O(\sqrt{n})$次移动就可以得出结论。
官方标程是用双指针模拟求解，复杂度为$O(n)$，但是可以利用单调栈$O(\sqrt{n})$预处理然后$O(1)$查询。
最终时间复杂度为$O(n+\sqrt{n})$。

#include

#define si(a) scanf("%d",&a)
#define sl(a) scanf("%lld",&a)
#define sd(a) scanf("%lf",&a)
#define sc(a) scahf("%c",&a);
#define ss(a) scanf("%s",a)
#define pi(a) printf("%d\n",a)
#define pl(a) printf("%lld\n",a)
#define pc(a) putchar(a)
#define ms(a) memset(a,0,sizeof(a))
#define repi(i, a, b) for(register int i=a;i<=b;++i)
#define repd(i, a, b) for(register int i=a;i>=b;--i)
#define reps(s) for(register int i=head[s];i;i=Next[i])
#define ll long long
#define ull unsigned long long
#define vi vector
#define pii pair
#define mii unordered_map
#define msi unordered_map
#define lowbit(x) ((x)&(-(x)))
#define ce(i, r) i==r?'\n':' '
#define pb push_back
#define fi first
#define se second
#define all(x) x.begin(),x.end()
#define INF 0x3f3f3f3f
#define pr(x) cout<<#x<<": "<
using namespace std;

inline int qr() {
    int f = 0, fu = 1;
    char c = getchar();
    while (c < '0' || c > '9') {
        if (c == '-')fu = -1;
        c = getchar();
    }
    while (c >= '0' && c <= '9') {
        f = (f << 3) + (f << 1) + c - 48;
        c = getchar();
    }
    return f * fu;
}

const int N = 1e5 + 10;

int head[N], ver[N << 1], Next[N << 1], tot;
int n, a, b, T, d[N], f[N][3], len;
vi seq, stl, str;

inline void add(int x, int y) {
    ver[++tot] = y;
    Next[tot] = head[x];
    head[x] = tot;
}

inline void init() {
    memset(head, 0, sizeof(int) * n + 10);
    repi(i, 1, n)repi(j, 0, 2)f[i][j] = 0;
    tot = 0, seq.clear(), stl.clear(), str.clear();
}

inline void addv(int x, int v) {
    int pos = -1;
    repi(i, 0, 2)if (v >= f[x][i]) {
            pos = i;
            break;
        }
    if (pos == -1)return;
    repd(i, 2, pos + 1)f[x][i] = f[x][i - 1];
    f[x][pos] = v;
}

void dfs1(int x, int fa, int dep) {
    d[x] = 0;
    if (x == b)len = dep;
    reps(x) {
        int y = ver[i];
        if (y == fa)continue;
        dfs1(y, x, dep + 1), addv(x, d[y] + 1), d[x] = max(d[x], d[y] + 1);
    }
}

bool dfs2(int x, int fa) {
    if (f[x][2] >= len)return true;
    reps(x) {
        int y = ver[i];
        if (y == fa)continue;
        addv(y, f[x][d[y] + 1 == f[x][0]] + 1);
        if (dfs2(y, x))return true;
    }
    return false;
}

bool dfs3(int x, int fa) {
    bool flag = (x == b);
    d[x] = 0;
    reps(x) {
        int y = ver[i];
        if (y == fa)continue;
        if (dfs3(y, x))flag = true;
        else d[x] = max(d[x], d[y] + 1);
    }
    if (flag)seq.pb(x);
    return flag;
}

int main() {
    T = qr();
    while (T--) {
        n = qr(), a = qr(), b = qr();
        init();
        repi(i, 1, n - 1) {
            int x = qr(), y = qr();
            add(x, y), add(y, x);
        }
        dfs1(a, 0, 0);
        if (!dfs2(a, 0)) {
            puts("NO");
            continue;
        }
        dfs3(a, 0);
        repi(i, 0, len) {
            stl.pb(stl.empty() || d[seq[i]] - i > stl.back() ? d[seq[i]] - i : stl.back());
            str.pb(str.empty() || d[seq[len - i]] - i > str.back() ? d[seq[len - i]] - i : str.back());
        }
        reverse(all(str));
        int l = 0, r = len;
        while (l < r) {
            if (l < str[r])l = str[r];
            else if (len - r < stl[l])r = len - stl[l];
            else break;
        }
        puts(l >= r ? "YES" : "NO");
    }
    return 0;
}