图论(九)最小生成树-Kruskal算法
前面说过,Kruskal是从最短边着手构建最小生成树的。其基本过程是:先对图中的所有边按照权重值从小到大进行排序,然后着手选取边构建最小生成树。如果直接从小到大按顺序选取,有可能形成了环,所以对环的处理就成了核心问题。
我们还是以前面的乡镇假设光纤网络为例:
Kruskal算法工作步骤如下:
(1) 将边进行排序。
| Begin |
End |
Weight |
| e |
i |
7 |
| c |
h |
8 |
| a |
b |
10 |
| a |
f |
11 |
| b |
g |
12 |
| b |
h |
12 |
| d |
i |
16 |
| f |
g |
17 |
| b |
d |
18 |
| g |
i |
19 |
| d |
e |
20 |
| d |
h |
21 |
| c |
d |
22 |
| d |
g |
24 |
(2) 按权重依次从小到大将边加入最小生成树。
我们依次将边e-i(7),c-h(8),a-b(10),a-f(11),b-g(12),b-h(12),d-i(16)加入最小生成树中(图中标绿色的边),到目前为止,没有任何问题。
(3) 检查新加入的边是否构成了环。
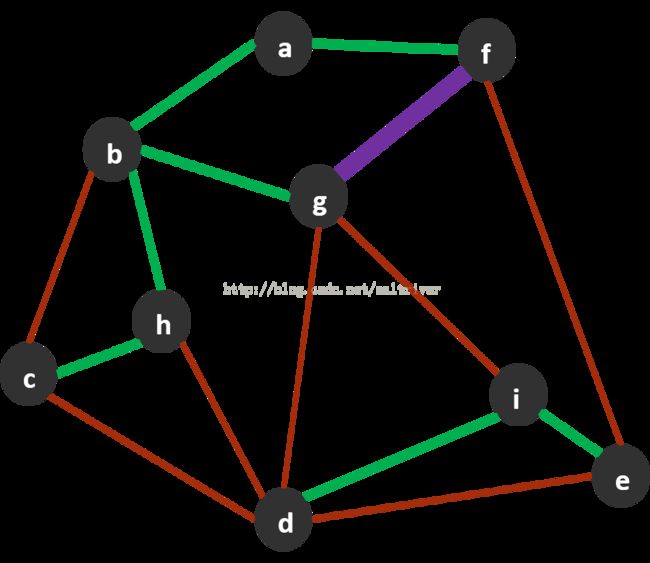
下面,按照顺序需要将边f-g(17)加入最小生成树。
很不幸,这时a-b-g-f-a构成了环。于是f-g(17)被排除,不能被加入最小生成树。
下面按顺序加入的边是b-c(18),同样b-c-g-b也构成了环,所以边b-c(18)也被排除。如此依次类推,最后得到的最小生成树是:
好了,算法介绍完了。就这么简单!
当然,这里有个核心问题还没有清楚的描述,即怎样判断构成了环?
判断原理也很简单:最小生成树加入一条边从而构成环,那么这条边的两个顶点除了这条边外,必然还有另一条路径,即这两个顶点在加入这个边之前,就是连通的,或者在一个连通子图上。
因此,在G=(V,E)中,我们令最小生成树的初始状态为只有n个顶点,0条边的非连通图T=(V,{}),图中每个顶点都是一个连通子图,即有n个连通子图。依次从E中按顺序从小到大选择边,若该边的两个顶点落在T中不同的连通子图上,则将次变加入到T中,否则舍去此边,依次类推,直到T中所有顶点都在同一个连通子图上为止。
光说不练假把式。上代码:
# -*- coding: utf-8 -*-
# 构建图G,使用了邻接矩阵表示法,9999代表非直连
G =[[0,10,9999,9999,9999,11,9999,9999,9999], # a的邻居表
[10,0,18,9999,9999,9999,12,12,9999], # b的邻居表
[9999,18,0,22,9999,9999,9999,8,9999], # c的邻居表
[9999,9999,22,0,20,9999,24,21,16], # d的邻居表
[9999,9999,9999,20,0,26,9999,9999,7], # e的邻居表
[11,9999,9999,9999,26,0,17,9999,9999], # f的邻居表
[9999,12,9999,24,9999,17,0,9999,19], # g的邻居表
[9999,12,8,21,9999,9999,9999,0,9999], # h的邻居表
[9999,9999,9999,16,7,9999,19,9999,0]] # i的邻居表
# 构建顶点序号与符号对应集
v_dict ={}
v_strdict ={}
v_str ='abcdefghi'
for iin range(len(G)):
v_dict[i]= v_str[i]
for i, valuein enumerate(v_str):
v_strdict[value]= i
# 构建边集
E =[(v_dict[u], v_dict[v], G[u][v]) for uin range(len(G))for vin range(len(G[u]))if 0< G[u][v]< 9999and u< v]
# 对边集进行排序
E =sorted(E,key=lambdax:x[2])
# 构建最小生成树
T =set()
# 构建顶点连通子图
V =[0]* len(G)
# 判断是否属于同一连通子图
def find_connect(V,v):
whileV[v]> 0:
v= V[v]
returnv
# 循环边
for ein E:
#边的两个顶点是否已连通
v1, v2= find_connect(V, v_strdict[e[0]]), find_connect(V, v_strdict[e[1]])
ifv1 !=v2:
V[v1]= v2
T.add(e) #将边加入最小生成树
# 输出最小生成树
print(T)
# 输出代价
print(sum([t[2]for tin T]))
输出结果:
{('e', 'i', 7), ('g', 'i', 19), ('c', 'h', 8), ('a', 'f', 11), ('b', 'g', 12), ('d', 'i', 16), ('a', 'b', 10), ('b', 'h', 12)}
95
该算法的主要执行过程在最后的for循环处,find_connect函数与顶点的个数V决定,时间复杂度为O(logV),而外面是边E的循环,因此Kruskal算法的时间复杂度为O(E logV)。