花里胡哨der惹某第12周周记（习题+感悟）

（一）2019 ICPC Asia Nanjing Regional

计蒜客上出了重现赛，就和队友（两位巨佬一起打了一手，结果被紫妈的一人队打压了，难顶噢）

A - Hard Problem

题目描述

    Given a positive integer n, you need to find out the minimum integer k such that for any subset T of the set {1,2,⋯,n} of size k, there exist two different integers u,v∈ T that u is a factor of v.

Input

    The first line contains an integer T (1≤T≤1e5) indicating the number of test cases.
    Each of the following T lines contains an integer n (2≤n≤1e9) describing a test case.

Output

    For each test case, output a line containing an integer which indicates the answer.

Sample Input

4
2
3
4
5

Sample Output

2
3
3
4

理解

 开题看了A（悄悄说因为队里的思维大佬写过这题）然后分析了一波（本来以为是质数-1）
 划掉，然后发现这样想太复杂了
 小姐姐直接说出了她之前发现的规律，然后直接A了（躺赢）

AC代码

#include
using namespace std;

int main(){
	int T;
	scanf("%d", &T);
	while(T--){
		int n;
		scanf("%d", &n);
		if(n % 2 == 0){
			printf("%d\n", (n - 2) / 2 + 2);
		}else{
			printf("%d\n", (n - 1) / 2 + 2);
		}
	}
	return 0;
}

B - Prince and Princess

题目描述

    Prince Mochi of the Mochi Kingdom falls in love with Princess Tofu of the Tofu Kingdom, but the queen of the Tofu Kingdom does not assent to this marriage.
    The queen challenges their love and advocates a task for Prince Mochi. Solving this task is the premise for earning their happiness. The lack of capacity obliges Prince Mochi to ask you for help.
    Here is the task: Princess Tofu, King Tofu, the queen, the minister, maids, chefs, and many others are all together for the task, all staying in separate rooms. Note that there is no empty room. Each one of them knows where he/she is and where any other people are.
    Prince Mochi is asked to find the princess. He can inquire anyone about the following three types of questions:
            ·Who are you?
            ·Who is staying in a specified room?
            ·Which room does the Princess Tofu stay in?
    They will never refuse to answer the questions, but may not tell the truth. People, including Princess Tofu herself, who support this marriage will present the facts. The opposition, like the queen, will always provide an incorrect answer. Other participants will be arbitrary.
    Prince Mochi does not want to spend too much time and so he will query as little as possible. Can you tell him the minimum number of questions he really needs to confirm where his darling is under any circumstances? But sometimes, the task is impossible, then you should also remind him to begin a new love affair.

Input

    The only line in input contains three integers a (1≤a≤2×1e5), b and c(0≤b,c≤2×1e5) which represent the number of participants who support this marriage, who are against this marriage and who do not really care about it respectively.

Output

    If it is impossible to determine where Prince Mochi is, output NO. Otherwise, output YES at first following an integer indicating the minimum number of questions the prince needs to inquire in the second line.

Sample Input

样例输入1
2 0 0
样例输入2
1 1 0

Sample Output

样例输出1
YES
1
样例输出2
NO

Hint

样例解释2：
In the second sample case, Prince Mochi may ask all available questions to both participants. However, in the case when they always provide the same answer, the prince cannot ensure where the princess is. Thus the answer is NO.

理解

 题目大致意思是有a个人会说真话，b个人说假话，c个人不确定说的话是真是假
 第一眼看到这题还以为是博弈论，当场觉得头疼
 后来看到了题目里提到了YES是百分百确定找到公主
 所以按照最坏情况来考虑假设c个人说的都是假话，假设先问到了说假话的b+c个人
 那么只需要再问b+c+1个说真话的人，就可以找到真正的公主啦
 值得注意的是1 0 0这组样例要特判一下，只有一个人那就肯定是公主，所以不用询问啦

AC代码

#include
using namespace std;

int main(){
	int a,b,c;
	scanf("%d %d %d",&a,&b,&c);
	if(a == 1 && b == 0 && c == 0){
		printf("YES\n0\n");
	}
	else{
		if(a > b + c){
			printf("YES\n");
			printf("%d\n", 2 * (b + c) + 1);
		}else{
			printf("NO\n");
		}
	}
	return 0;
}

C - Triangle

题目描述

    One day, ABC and DD found a triangular wheat field, and they decide to cut it into two pieces with the same area with a segment. Because of various reasons, one of the endpoints of the division line is fixed at (px, py). Now you are asked to find the other endpoint of the segment.
    If the given endpoint does not lie on the boundary of the wheat field, the problem should be regarded as invalid. The other endpoint required should also locate on the boundary.

Input

    The input provides several test cases and the first line of the input contains a single integer T (1≤T≤1000000) indicating the number of cases.
    For each test case, eight integers x1,y1,x2,y2,x3,y3,px are given in a line, where (x1,y1),(x2,y2) and (x3,y3) describe the coordinates of vertices for the given triangle wheat field which are guaranteed to be not colinear, and (px,py) is the given endpont of the segment. All coordinates are integers in the range [0,100000].

Output

    For each test case, output the coordinate of the other endpoint of the division segment, or output the number -1 if the problem, in this case, is invalid.
    Formally, if your answer is a and the jury’s answer is b, then your answer will be considered correct if and only if |a - b| / max{1, |b|} ≤1e6.

Sample Input

2
0 0 1 1 1 0 1 0
0 0 1 1 1 0 2 0

Sample Output

0.500000000000 0.500000000000
-1

理解

这题本来想用笨笨的数学大法，算三条线的斜率然后判断p点在哪条线上，然后继续判断q
q在相邻的哪条边上，然后根据在算坐标
实在是太麻烦了，绕来绕去都晕了（哭辽）
聪明的zlb同学直接拉了一个向量的板子，解决了令人苦恼的问题
诸如斜率不存在，以及判断是否在线上，以及直线公式计算，板子真香
然后我们判断了p在那条线，找离远的点为顶点的那条边去找q
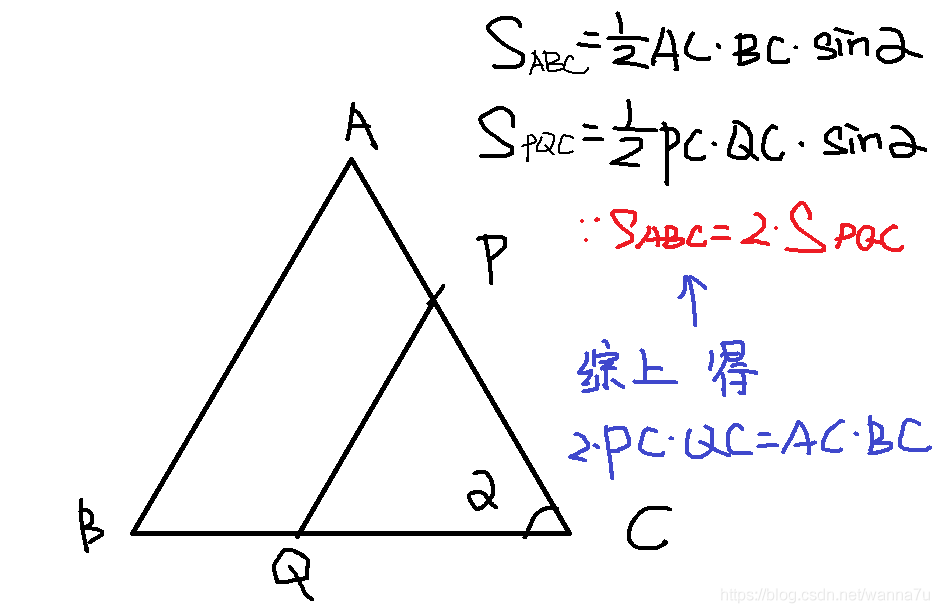
之前还推了一个pq到同个顶点的公式，如下图：

图画的丑且草率。。。请不要介意
就是乳齿的神奇，然鹅判完p判q的判断着实令人绕晕，，应该还有更简单的方法吧
然后根据上图算出q到顶点的长度 根据长度比例直接算坐标就ok啦
wa了一发是因为光顾着判断p是否合法，忘记判断q是否合法了（略略略）
再说一次 向量板子真香

AC代码

#include
using namespace std;
const double eps = 1e-8;
const double inf = 1e20;
const double pi = acos(-1.0);
const int maxp = 1010;
//Compares a double to zero
int sgn(double x){
	if(fabs(x) < eps)return 0;
	if(x < 0)return -1;
 	else return 1;
}
 //square of a double
inline double sqr(double x){return x*x;}
struct Point{
	double x,y;
	Point(){}
	Point(double _x,double _y){
		x = _x;
		y = _y;
	}
	void input(){
		scanf("%lf%lf",&x,&y);
	}
	void output(){
		printf("%.2f %.2f\n",x,y);
	}
	bool operator == (Point b)const{
		return sgn(x-b.x) == 0 && sgn(y-b.y) == 0;
	}
	bool operator < (Point b)const{
		return sgn(x-b.x)== 0?sgn(y-b.y)<0:x<b.x;
	}
	Point operator -(const Point &b)const{
		return Point(x-b.x,y-b.y);
	}
	double operator ^(const Point &b)const{
		return x*b.y - y*b.x;
	}
	//µã»ý
	double operator *(const Point &b)const{
		return x*b.x + y*b.y;
	}
	//·µ»Ø³¤¶È
	double len(){
		return hypot(x,y);//¿âº¯Êý
	}
	//·µ»Ø³¤¶ÈµÄƽ·½
	double len2(){
		return x*x + y*y;
	}
	//·µ»ØÁ½µãµÄ¾àÀë
	double distance(Point p){
		return hypot(x-p.x,y-p.y);
	}
	Point operator +(const Point &b)const{
		return Point(x+b.x,y+b.y);
	}
	Point operator *(const double &k)const{
		return Point(x*k,y*k);
	}
	Point operator /(const double &k)const{
		return Point(x/k,y/k);
	}
	//¼ÆËã pa ºÍ pb µÄ¼Ð½Ç
	//¾ÍÊÇÇóÕâ¸öµã¿´ a,b Ëù³ÉµÄ¼Ð½Ç
	//²âÊÔ LightOJ1203
	double rad(Point a,Point b){
		Point p = *this;
		return fabs(atan2( fabs((a-p)^(b-p)),(a-p)*(b-p) ));
	}
	//»¯Îª³¤¶ÈΪ r µÄÏòÁ¿
	Point trunc(double r){
		double l = len();
		if(!sgn(l))return *this;
		r /= l;
	 	return Point(x*r,y*r);
	 }
 };
 struct Line{
	Point s,e;
 	Line(){}
 	Line(Point _s,Point _e){
 		s = _s;
 		e = _e;
 	}
 	bool operator ==(Line v){
 		return (s == v.s)&&(e == v.e);
 	}
 	int relation(Point p){
		int c = sgn((p-s)^(e-s));
 		if(c < 0)return 1;
 		else if(c > 0)return 2;
 		else return 3;
 	}
};
int main()
{
	int T;
	scanf("%d", &T);
	while(T--){
		double x1,x2,x3,y1,y2,y3,px,py;
		scanf("%lf %lf %lf %lf %lf %lf %lf %lf",&x1,&y1,&x2,&y2,&x3,&y3,&px,&py);
		Point s1(x1, y1), s2(x2, y2), s3(x3, y3), p(px, py);
		Line li1(s1, s2), li2(s2, s3), li3(s1, s3);
		double dis12 = s1.distance(s2);
		double dis13 = s1.distance(s3);
		double dis23 = s2.distance(s3);
		if(li1.relation(p) == 3 && abs(s1.distance(p) + s2.distance(p) - dis12) <= eps){
			if(s1.distance(p) > s2.distance(p)){
				double d = dis12 * dis13 / s1.distance(p) / 2.0;
				double xq = x1 - (x1 - x3) * (d / dis13);
				double yq = y1 - (y1 - y3) * (d / dis13);
				Point q(xq, yq);
				if(abs(s1.distance(q) + s3.distance(q) - dis13) > eps){
					printf("-1\n");
					continue;
				}
				printf("%.12lf %.12lf\n", xq, yq);
				continue;
			}else{
				double d = dis12 * dis23 / s2.distance(p) / 2.0;
				double xq = x2 - (x2 - x3) * (d / dis23);
				double yq = y2 - (y2 - y3) * (d / dis23);
				Point q(xq, yq);
				if(abs(s2.distance(q) + s3.distance(q) - dis23) > eps){
					printf("-1\n");
					continue;
				}
				printf("%.12lf %.12lf\n", xq, yq);
				continue;				
			}
		}else if(li2.relation(p) == 3 && abs(s2.distance(p) + s3.distance(p) - dis23) <= eps){
			if(s2.distance(p) > s3.distance(p)){
				double d = dis12 * dis23 / s2.distance(p) / 2.0;
				double xq = x2 - (x2 - x1) * (d / dis12);
				double yq = y2 - (y2 - y1) * (d / dis12);
				Point q(xq, yq);
				if(abs(s1.distance(q) + s2.distance(q) - dis12) > eps){
					printf("-1\n");
					continue;
				}
				printf("%.12lf %.12lf\n", xq, yq);
				continue;				
			}else{
				double d = dis13 * dis23 / s3.distance(p) / 2.0;
				double xq = x3 - (x3 - x1) * (d / dis13);
				double yq = y3 - (y3 - y1) * (d / dis13);
				Point q(xq, yq);
				if(abs(s1.distance(q) + s3.distance(q) - dis13) > eps){
					printf("-1\n");
					continue;
				}
				printf("%.12lf %.12lf\n", xq, yq);
				continue;				
			}
		}else if(li3.relation(p) == 3 && abs(s1.distance(p) + s3.distance(p) - dis13) <= eps ){
			if(s1.distance(p) > s3.distance(p)){
				double d = dis13 * dis12 / s1.distance(p) / 2.0;
				double xq = x1 - (x1 - x2) * (d / dis12);
				double yq = y1 - (y1 - y2) * (d / dis12);
				Point q(xq, yq);
				if(abs(s1.distance(q) + s2.distance(q) - dis12) > eps){
					printf("-1\n");
					continue;
				}			
				printf("%.12lf %.12lf\n", xq, yq);
				continue;				
			}else{
				double d = dis13 * dis23 / s3.distance(p) / 2.0;
				double xq = x3 - (x3 - x2) * (d / dis23);
				double yq = y3 - (y3 - y2) * (d / dis23);
				Point q(xq, yq);
				if(abs(s2.distance(q) + s3.distance(q) - dis23) > eps){
					printf("-1\n");
					continue;
				}	
				printf("%.12lf %.12lf\n", xq, yq);
				continue;				
			}
		}else{
			printf("-1\n");
			continue;
		}
	} 
	return 0;
}

D - Digital Path

题目描述

    Zhe the bully, is condemned by all kinds of evil, like bullying those who are weaker. His teammates have been mistreated for a long time. Finally, they decided not to put up with their buddy any more and flee to Digital Village, with the bully in hot pursuit. Due to difficult terrain and a considerable amount of Digital Paths staggered, they can’t be easily arrested.
    Getting familiar with the terrain as soon as possible is important for these innocents to escape the threat of bullying. All they need now is to count the number of Digital Paths in Digital Village.
    To simplify the problem, Digital Village is abstracted into a grid with nn rows and mm columns filled by integers. A Digital Path is a continuous walk in the grid satisfying the following conditions:
        ·adjacent boxes in the walk share a common edge;
        ·the walk is maximal, which cannot be extended;
        ·the walk contains at least four boxes;
        ·going from one end to the other, the increment of values for any two adjacent boxes is exactly one.
    Here we have some examples.

    The path in Figure 1 is invalid because its length is less than 44.

    The path in Figure 2 is invalid because it is not continuous.

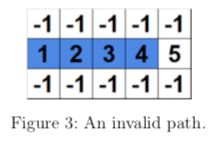
    The path in Figure 3 is invalid because it can be extended further.

    The path in Figure 4 is also invalid because values in the path are not strictly increased by one.

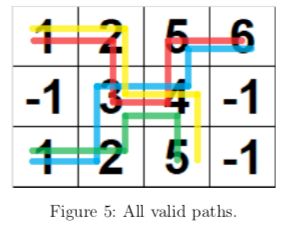
    Digital Paths may partially overlap. In Figure 5, there are 44 Digital Paths marked by different colours.

Input

    The first line contains two positive integers n and m (1≤n,m≤1000) describing the size of the grid.
Each of the next nn lines contains mm integers, the jj-th of which, denoted by a(i,j)(-1e7 <= a(i,j) <= 1e7) represents the value of the box in the i-th row and the j-th column.

Output

    Output the number of Digital Paths modulo (1e9+7).

Sample Input

样例输入1
3 5
1 2 3 8 7
-1 -1 4 5 6
1 2 3 8 7
样例输入2
4 4
1 2 3 4
2 3 4 3
3 4 3 2
4 3 2 1

Sample Output

样例输出1
4
样例输出2
16

理解

首先看到题目的数据大小下了一个强行dfs必定tle的定律，然后以为能dp
结果发现并不能（然后提出了赋值递推的想法）
最起先没有好好理解题意(-1e7 <= a(i,j) <= 1e7) ！！！！！划个重点（好好读题）
题目的意思是可以从任意一个数字开始 ，连续4步才能算得上是一条路！！！
最起先理解错了就很难顶，导致wa了好几发，其中也有不好好在中途取模的锅
然后代佬给出了先判断该点是不是起始点（及四周没有他的值-1的点）然后往后搜索值+1的点
至少得有四个，给四个后的那个点权值+1（及有一条路可以通往）
如果这个点四周有比它值-1的点说明之前已经搜过了，直接传递权值即可
最初的处理就是把所有的点按大小从小到大排起来存一个结构体
dfs只需要step>=4即可（就可以省时间啦）
然后往四周传值后记得该点清零嗷，最后跑一遍n*n全加起来，（有权值的都是结束点）
就得出答案啦！一定要记得中途取模嗷！取模取模取模（重要的事情说三遍）

AC代码

#include
using namespace std;
const int maxn = 1010;
int a[maxn][maxn];
int n, m;
long long val[maxn][maxn];
const int mod = 1e9 + 7;
struct node{
	int x, y, val;
	node(int _x, int _y, int _val){
		x = _x;
		y = _y;
		val = _val;
	}
};
vector < node > g;
int dx[6] = {0, 0, 0, -1, 1};
int dy[6] = {0, 1, -1, 0, 0};
bool cmp(node a , node b)
{
	if(a.val != b.val){
		return a.val < b.val;
	}else if(a.x != b.x){
		return a.x < b.x;
	}else{
		return a.y < b.y;
	}
}
void dfs(int x, int y, int step)
{
	if(step >= 4){
		val[x][y] = (val[x][y] + 1) % mod;
		return ;
	}
	for(int i = 1; i <= 4; i++){
		int nx = x + dx[i];
		int ny = y + dy[i];
		if(nx < 1 || nx > n || ny < 1 || ny > m)
			continue;
		if(a[nx][ny] == a[x][y] + 1){
			dfs(nx, ny, step + 1);
		}
	}
}
bool check(int x, int y, int val)
{
	for(int i = 1; i <= 4; i++){
		int nx = x + dx[i];
		int ny = y + dy[i];
		if(nx < 1 || nx > n || ny < 1 || ny > m)
			continue;
		if(a[nx][ny] == a[x][y] - 1){
			return 0;
		}
	}
	return 1;
}
int main()
{
	scanf("%d %d", &n, &m);
	for(int i = 1; i <= n; i++){
		for(int j = 1; j<= m; j++){
			scanf("%d", &a[i][j]);
			g.push_back(node(i, j, a[i][j]));
		}
	}
	long long ans = 0;
	sort(g.begin(), g.end(), cmp);
	for(int i = 0; i < g.size(); i++){
		node w = g[i];
		int x = w.x, y = w.y;
		if(check(x, y, a[x][y])){
			dfs(x, y, 1);
		}else{
			int flg = 0;
			for(int i = 1; i <= 4; i++){
				int nx = x + dx[i];
				int ny = y + dy[i];
				if(a[nx][ny] == a[x][y] + 1){
					flg = 1;
					val[nx][ny] += val[x][y];
					val[nx][ny] %= mod;
				}
			}
			if(flg == 1){
				val[x][y] = 0;
			}				
		}
	}
	for(int i = 1; i <= n; i++){
		for(int j = 1; j <= m; j++){
			ans = (ans + val[i][j]) % mod;
		}
	}
	printf("%lld\n", ans);
	return 0;
}

（二）杂七杂八的der题目集合

A - Colorful Hats 2 (来源Actoder1201场E题)

题目描述

    N people are standing in a queue, numbered 1,2,3,…,N from front to back. Each person wears a hat, which is red, blue, or green.
The person numbered i says:“In front of me, exactly Ai people are wearing hats with the same color as mine.”
    Assuming that all these statements are correct, find the number of possible combinations of colors of the N people’s hats.
    Since the count can be enormous, compute it modulo 1000000007.
Constraints
    1≤N≤100000
    0≤Ai≤N−1
    All values in input are integers.

Input

Input is given from Standard Input in the following format:
N
A1 A2 A3 … AN

Output

Print the number of possible combinations of colors of the N people’s hats, modulo 1000000007.

Sample Input

Sample Input 1
6
0 1 2 3 4 5
Sample Input 2
3
0 0 0
Sample Input 3
54
0 0 1 0 1 2 1 2 3 2 3 3 4 4 5 4 6 5 7 8 5 6 6 7 7 8 8 9 9 10 10 11 9 12 10 13 14 11 11 12 12 13 13 14 14 15 15 15 16 16 16 17 17 17

Sample Output

Sample Output 1
3
Sample Output 2
6
Sample Output 3
115295190

理解

这题的意思就是一共n个人
每个人能看到前面有多少人和他的帽子一样
然后本来一脸迷茫，直到优秀的同学给出了如下的优秀方法
因为只有三种颜色，所以每个数字只要往前推三个，看有没有哪个可能是他继承过来的位置
然后记录有多少种可能，相加可能然后*上去
然后开b数组存三种颜色分别变成了数字几
由此可以判断不存在的情况输出-1

AC代码

#include
using namespace std;
typedef long long ll;
const int mod = 1e9 + 7;
const int maxn = 1e5 + 7;
int b[5];
int a[maxn];
int main(){
	int n;
	scanf("%d",&n);
	ll ans = 1;
	memset(b,0,sizeof(b));
	for(int i = 1;i <= n;i++) scanf("%d",&a[i]);
	for(int i = 1;i <= n;i++){
		int val = a[i];
		int cnt = 0;
		for(int j = 1;j <= 3;j++){
			if(b[j] == val){
				cnt++;
			}
		}
		ans = (ans * cnt) % mod;
		for(int j = 1;j <= 3;j++){
			if(b[j] == val){
				b[j]++;
				break;
			}
		}
	}
	printf("%lld\n",ans);
	return 0;
}

（三）我的感想（我好菜鸭）

关于这周的日常练习

很充实的一周，蓝桥杯校赛（虽然打得很烂，，，）OJ赛制也太难了吧，有个找规律的题目，想记录，无奈没有题目，难顶。然后还去宁理打了校赛，很想记录那个C题，是我不好好读题的锅，没有看到min(2,n)，读错题我也太难了，，，被中学生按着摩擦，就很难受，不过ACM菜是原罪，和两位大佬配合打了一下南京的重现赛，感受到了自己的思维能力不行以及我是个有点鸡肋的存在，往往是一起分析题意，但是别人的想法是更优解，码代码的速度也不太来塞，往往觉得一个问题在已知的情况下无解（或者是说难解），需要板子的时候，对于板子不太理解，就是这样没错了。打算开一下DP这块的内容，听紫妈说是很难，且类别多，头插DP，状压DP且是对于到时候，不仅是套个DP板子就能有解的，码题算是理解DP，到时候得自己结合实际推公式（希望自己思维能够跟得上吧）CF上是日常的疯狂掉分，，打到睡着，有一个憨憨错法的题目，改对了就不记录了，错的太过于憨批，，，华师大的月赛更是写的出来的人均能写，难题只有寥寥数人能A，这个差距吧就不言而喻了。