背景
呵呵。有没有人能解释一下为什么NOIP会考圆方树????
那NOI考什么???????
DALAO1:
有难度的仙人掌题在近几年也只是在国家集训队水平的比赛里才会出现。
不过,这不是说仙人掌对国集水平以下的选手意义不大:
首先,仙人掌暴力 DP 问题难度并不大,在省选、 NOI 甚至 NOIP 中可能出现;
其次,仙人掌问题的处理能很好锻炼选手的特殊情况全面考虑并正确处理的能力,提升对超长代码的把握;
DALAO2:
近年来,仙人掌在各大OI竞赛中的出现逐渐频繁,虽然仙人掌本身就有一些特殊而优美的性质,但我们终究是没有很多针对仙人掌的算法,就使得很多仙人掌的题变得很棘手。
都9102年了,怎么还能跟2018年相比呢?当然什么都会考啊?
QAQ
菜鸡学圆方树没前途。【亲身实测
我们都知道,在图论里面有一种很难搞的图---菊花图。【或许并没有很难搞?
然而还有一种更加奇怪特殊的图----仙人掌图
仙人掌图
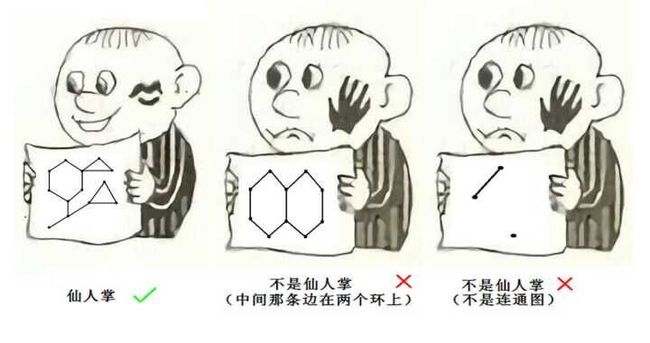
仙人掌图就是长得像仙人掌的图嘛 【还挺像的
定义:对一个无向连通图,任意一条边属于至多一个简单环。
-
- 桥边:非环边,就是连接环的那些边;
- 环边:就是环中的边嘛。
在仙人掌上,父亲和儿子都有节点的和环的之分。
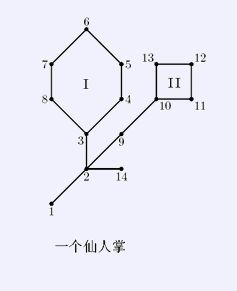
然后我从网上搞了张经典图。
于是乎,我们获得了一张仙人掌图。
对于一个仙人掌,任意构建出一棵生成树。
然后我们就多了一些边——可以叫返祖边或者随便什么名字。
因为每条边只会出现在一个环中,所以每条返祖边都会覆盖树中的一条链,这条链+这条边构成了环。
所以我们可以确定每条边都出现在了哪个环中。
好像没啥特殊的地方啊 ?
比如仙人掌的最大独立集,DP的时候只要额外的记录一下所在环的返祖边的端点的状态就ok。
似乎要锅?
我们来看一个例题吧。
例题
一颗仙人掌,每条边有边权,求1号节点到每一个节点的最短路的长度。节点个数 n<=1e5
算法简述
我只简述一下,毕竟只是一个引例。
我们 DFS 可以得到一颗 DFS 树。
判断环和桥,然后分别 DP 处理。
遍历每条边时如果 low[v] 大于 dfn[u] ,说明此边为树边;然后就可以DP
对于一个环,把它缩成一个点(即把一个环的 f 信息都存在其根上),然后就可以按之前的方式 DP
但是环中更新答案的时候只转一圈不能保证答案最优【因为有可能最优的那一部分环被根分开了
又由于环中距离的定义是最短路,所以我们只要转够一圈半即可。
通过上面的一系列分析,我们可以发现:
仙人掌问题的解决方法也不过就是参照树的解法,然后特判环上的情况【把环上的信息记录到一个点上
那么我们为什么不直接把仙人掌图变成一棵树呢?这样不是更方便嘛?
事实证明,你能想到的,大佬前辈们都想到了。
这就是圆方树。
圆方树
什么是圆方树?
顾名思义,这是一颗有圆点又有方点的树。
圆点就是原仙人掌中所有的点,方点是我们新添加进去的点。
条件简陋,没法自己画图QAQ
首先,我们先来考虑怎么样把一张仙人掌变成圆方树。
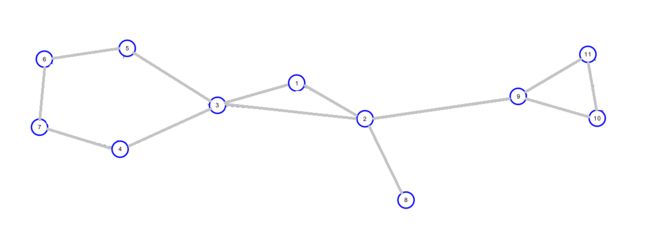
先有一盆仙人掌。
如果一条边在仙人掌中不属于任何一个环中,那么它直接圆方树中的两个圆点。
对于仙人掌中的任意一个环,则每个环上的点在圆方树上对应的圆点向这个环对应的方点连边。
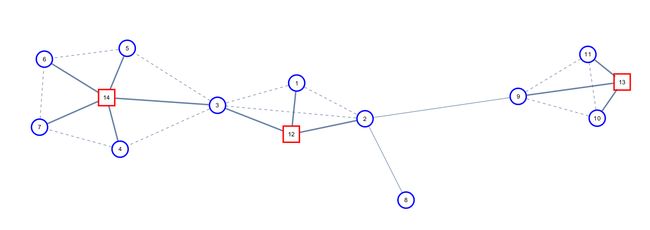
然后我们得到了下面这个。
然后就获得了一颗圆方树。
怎么证明这是一颗树呢?
DALAO的博客里面有下面这段话。
orz,我康不懂。
翻译成人话就是:连通图上面,点数=边数+1
然鹅证明并不重要。
重要的是性质。
圆方树的性质
1.无论如何换根,圆方树形态不变
证明:显然。
2.方点不会和方点相连
证明:也显然。
3.圆方树的子树=原仙人掌的子仙人掌
子仙人掌 定义:
以 r 为根的仙人掌上的点 p 的子仙人掌,是去掉 p 到 r 的所有简单路径之后, p 所在的连通块。
证明:
当 p 不在环上,显然成立。
否则,去除所有到达根节点的所有简单路径之后,剩下的只有和p相连的,并且和 p 不在一个环内的点。
显然是圆方树上 p 子树中的原点【和他在一个环内的原点都不和他相连了
总结
求仙人掌的最大独立集,求仙人掌直径,都可以使用普通做饭,只要在环上特殊判断一下就行。
但是求仙人掌两点间的最短路,就需要构建出圆方树,直接把圆方树树链剖分(也可以倍增求LCA)
圆点和圆点之间的边和原仙人掌是同构的,
我们知道方点的父亲一定是圆点(转换为有根树之后),
这样子把每条圆点和方点之间的边的权值赋为到达方点父亲的最短路径就好啦。
所以圆方树好难啊QAQ
广义圆方树
补充知识,广义圆方树。
对于一个一般的无向连通图来说,显然也可以用圆方树。
画个图我们发现:仙人掌上的圆方树是圆圆点之间是可能有边的。
但是在一张普通的图上面,失去了这个性质。
那么怎么办呢?
可以强制把两个点也看成一个点双。
题暂时还没写。QAQ我好菜啊