写在最前
本次分享一下通过实现kmp算法的动画效果来试图展示kmp的基本思路。
欢迎关注我的博客,不定期更新中——
前置概念
字符串匹配
字符串匹配是计算机科学中最古老、研究最广泛的问题之一。一个字符串是一个定义在有限字母表∑上的字符序列。例如,ATCTAGAGA是字母表∑ = {A,C,G,T}上的一个字符串。字符串匹配问题就是在一个大的字符串T中搜索某个字符串P的所有出现位置。
kmp算法
KMP算法是一种改进的字符串匹配算法,由D.E.Knuth,J.H.Morris和V.R.Pratt同时发现,因此人们称它为克努特——莫里斯——普拉特操作(简称KMP算法)。KMP算法的关键是利用匹配失败后的信息,尽量减少模式串与主串的匹配次数以达到快速匹配的目的。具体实现就是实现一个next()函数,函数本身包含了模式串的局部匹配信息。时间复杂度O(m+n)。
在js中字符串匹配我们通常使用的是原生api,indexOf;其本身是c++实现的不在这次的讨论范围中。本次主要通过动画演示的方式展现朴素算法与kmp算法对比过程的异同从而试图理解kmp的基本思路。
PS:在之后的叙述中BBC ABCDAB ABCDABCDABDE为主串;ABCDABD为模式串
效果预览
上方为朴素算法即按位比较,下方为kmp算法实现的字符串比较方式。kmp可以通过较少的比较次数完成匹配。
基本思路
从上图的效果预览中可以看出使用朴素算法依次比较模式串需要移位13次,而使用kmp需要8次,故可以说kmp的思路是通过避免无效的移位,来快速移动到指定的地点。接下来我们关注一下kmp是如何“跳着”移动的:
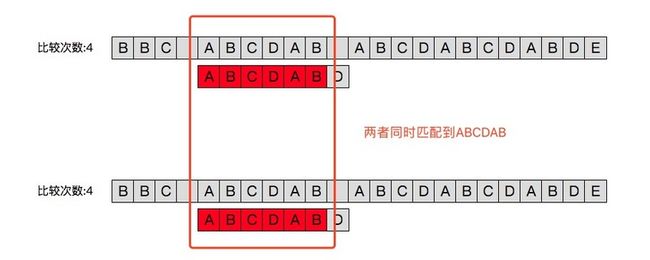
与朴素算法一致,在之前对于主串“BBC ”的匹配中模式串ABCBABD的第一个字符均与之不同故向后移位到现在上图所示的位置。主串通过依次与模式串中的字符比较我们可以看出,模式串的前6个字符与主串相同即ABCDAB;而这也就是kmp算法的关键。
根据已知信息计算下一次移位位置
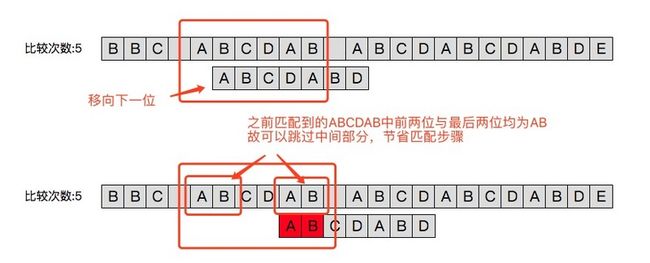
朴素算法雨打不动得向后移了一位。而kmp跳过了主串的BCD三个字符。从而进行了一次避免无意义的移位比较。那么它是怎么知道我这次要跳过三个而不是两个或者不跳呢?关键在于上一次已经匹配的部分ABCDAB
从已匹配部分发掘信息
我们已知此时主串与模式串均有此相同的部分ABCDAB。那么如何从这共同部分中获得有用的信息?或者换个角度想一下:我们能跳过部分位置的依据是什么?
第一次匹配失败时的情形如下:
BBC ABCDAB ABCDABCDABDE
ABCDABD
D != 空格 故失败为了从已匹配部分提取信息。现在将主串做一下变形:
ABCDABXXXXXX... X可能是任何字符我们现在只知道已匹配的部分,因为匹配已经失败了不会再去读取后面的字符,故用X代替。
那么我们能跳过多少位置的问题就可以由下面的解得知答案:
//ABCDAB向后移动几位可能能匹配上?
ABCDABXXXXXX...
ABCDABD答案自然是如下移动:
ABCDABXXXXXX...
ABCDABD因为我们不知道X代表什么,只能从已匹配的串来分析。
故我们能跳过部分位置的依据是什么?
答:已匹配的模式串的前n位能否等于匹配部分的主串的后n位。并且n尽可能大。
举个例子:
//第一次匹配失败时匹配到ABCDDDABC为共同部分
XXXABCDDDABCFXXX
ABCDDDABCE
//寻找模式串的最大前几位与主串匹配到的部分后几位相同,
//可以发现最多是ABC部分相同,故可以略过DDD的匹配因为肯定对不上
XXXABCDDDABCFXXX
ABCDDDABCE 现在kmp的基本思路已经很明显了,其就是通过经失败后得知的已匹配字段,来寻找主串尾部与模式串头部的相同最大匹配,如果有则可以跨过中间的部分,因为所谓“中间”的部分,也是有可能进入主串尾与模式串头的,没进去的原因即是相对位置字符不同,故最终在模式串移位时可以跳过。
部分匹配值
上面是用通俗的话来述说我们如何根据已匹配的部分来决定下一次模式串移位的位置,大家应该已经大体知道kmp的思路了。现在来引出官方的说法。
之前叙述的在已匹配部分中查找主串头部与模式串尾部相同的部分的结果我们可以用部分匹配值的说法来形容:
- 其中定义"前缀"和"后缀"。"前缀"指除了最后一个字符以外,一个字符串的全部头部组合;"后缀"指除了第一个字符以外,一个字符串的全部尾部组合。
- "部分匹配值"就是"前缀"和"后缀"的最长的共有元素的长度。
例如ABCDAB
- 前缀分别为A、AB、ABC、ABCD、ABCDA
- 后缀分别为B、AB、DAB、CDAB、BCDAB
很容易发现部分匹配值为2即AB的长度。从而结合之前的思路可以知道将模式串直接移位到主串AB对应的地方即可,中间的部分一定是不匹配的。移动几位呢?
答:匹配串长度 - 部分匹配值;本次例子中为6-2=4,模式串向右移动四位
代码实现
计算部分匹配表
function pmtArr(target) {
var pmtArr = []
target = target.split('')
for(var j = 0; j < target.length; j++) {
//获取模式串不同长度下的部分匹配值
var pmt = target
var pmtNum = 0
for (var k = 0; k < j; k++) {
var head = pmt.slice(0, k + 1) //前缀
var foot = pmt.slice(j - k, j + 1) //后缀
if (head.join('') === foot.join('')) {
var num = head.length
if (num > pmtNum) pmtNum = num
}
}
pmtArr.push(j + 1 - pmtNum)
}
return pmtArr
}kmp算法
function mapKMPStr(base, target) {
var isMatch = []
var pmt = pmtArr(target)
console.time('kmp')
var times = 0
for(var i = 0; i < base.length; i++) {
times++
var tempIndex = 0
for(var j = 0; j < target.length; j++) {
if(i + target.length <= base.length) {
if (target.charAt(j) === base.charAt(i + j)) {
isMatch.push(target.charAt(j))
} else {
if(!j) break //第一个就不匹配直接跳到下一个
var skip = pmt[j - 1]
tempIndex = i + skip - 1
break
}
}
}
var data = {
index: i,
matchArr: isMatch
}
callerKmp.push(data)
if(tempIndex) i = tempIndex
if(isMatch.length === target.length) {
console.timeEnd('kmp')
console.log('移位次数:', times)
return i
}
isMatch = []
}
console.timeEnd('kmp')
return -1有了思路后整体实现并不复杂,只需要先通过模式串计算各长度的部分匹配值,在之后的与主串的匹配过程中,每失败一次后如果有部分匹配值存在,我们就可以通过部分匹配值查找到下一次应该移位的位置,省去不必要的步骤。
所以在某些极端情况下,比如需要搜索的词如果内部完全没有重复,算法就会退化成遍历,性能可能还不如传统算法,里面还涉及了比较的开销。
参考文章
- 字符串匹配的KMP算法
最后
惯例po作者的博客,不定时更新中——
有问题欢迎在issues下交流。