PA1.2 代码+笔记
如果有什么地方有误 请多多指教;
写这个不是让同学们直接抄的,请弄懂原理哦,我觉得我解释的蛮清楚了。
遇到了问题也可以评论留言或者私信我;
pa1代码➕思路17元,pa2代码+思路30元,pa3仙剑奇侠传仅代码13元。扫码备注邮箱,一般立刻发,如果有事24小时内发。
1 PA1 – 开天辟地的篇章:最简单的计算机
1.2 表达式求值
数学表达式求值
词法分析
- 为token类型添加规则。
添加了空格== ( ) * / + - != && || ! 16进制10进制寄存器变量等16种规则。根据正则表达式,例如+*|\这些需要转义,所以+*|需要转义两次,第一次转义\,\再转义+*|。而其他字符不需要,可直接用ascii码代替。如&&、十进制等,运用正则表达式,并用enum给他们赋值。为了避免!=被识别为!和=的情况出现,我们将!=的顺序放在!前面。
代码如下:
enum {
TK_NOTYPE = 256, TK_EQ,TK_UEQ,TK_logical_AND,TK_logical_OR,TK_logical_NOT,TK_register,TK_variable,TK_number,TK_hex
/* TODO: Add more token types */
};
static struct rule {
char *regex;
int token_type;
} rules[] = {
/* TODO: Add more rules.
* Pay attention to the precedence level of different rules.
*/
{" +", TK_NOTYPE}, // spaces
{"==",TK_EQ}, // equal
{"\\(",'('}, // left parenthesis
{"\\)",')'}, // right parenthesis
{"\\*",'*'}, // multiplication
{"/",'/'}, // division
{"\\+",'+'}, // plus
{"-",'-'}, // subtraction
{"!=",TK_UEQ}, // unequal
{"&&",TK_logical_AND}, //logical AND
{"\\|\\|",TK_logical_OR}, //logical OR
{"!",TK_logical_NOT}, //logical NOT
{"0[xX][A-Fa-f0-9]{1,8}",TK_hex}, //hex
{"\\$[a-dA-D][hlHL]|\\$[eE]?(ax|dx|cx|bx|bp|si|di|sp)",TK_register}, //register
{"[a_zA_Z_][a-zA-Z0-9_]*",TK_variable}, //variable
{"[0-9]{1,10}",TK_number} //number
};
- make_token()函数。
识别出表达式中的单元token。该函数读取每个位置上的字符,通过for循环,用regexec函数匹配,和前面定义的rules[i]中的正则表达式比较,pmatch.rm_so==0表示匹配串在目标串中的第一个位置,pmatch.rm_eo表示结束位置,成功识别得到该字符或者字符串的对应规则后,用switch语句将表达式中每一个部分用对应的数字表示type,将==、十进制数等复制到tokens[nr_token].str中。
代码如下:
static bool make_token(char *e) {
int position = 0;
int i;
regmatch_t pmatch;
nr_token = 0;
while (e[position] != '\0') {
/* Try all rules one by one. */
for (i = 0; i < NR_REGEX; i ++) {
if (regexec(&re[i], e + position, 1, &pmatch, 0) == 0 && pmatch.rm_so == 0) {
char *substr_start = e + position;
int substr_len = pmatch.rm_eo;
Log("match rules[%d] = \"%s\" at position %d with len %d: %.*s",
i, rules[i].regex, position, substr_len, substr_len, substr_start);
position += substr_len;
/* TODO: Now a new token is recognized with rules[i]. Add codes
* to record the token in the array `tokens'. For certain types
* of tokens, some extra actions should be performed.
*/
switch (rules[i].token_type) {
case 257:
tokens[nr_token].type=257;
strcpy(tokens[nr_token].str,"==");
break;
case 40:
tokens[nr_token].type=40;
break;
case 41:
tokens[nr_token].type=41;
break;
case 42:
tokens[nr_token].type=42;
break;
case 47:
tokens[nr_token].type=47;
break;
case 43:
tokens[nr_token].type=43;
break;
case 45:
tokens[nr_token].type=45;
break;
case 258:
tokens[nr_token].type=258;
strcpy(tokens[nr_token].str,"!=");
break;
case 259:
tokens[nr_token].type=259;
strcpy(tokens[nr_token].str,"&&");
break;
case 260:
tokens[nr_token].type=260;
strcpy(tokens[nr_token].str,"||");
break;
case 261:
tokens[nr_token].type=261;
break;
case 262:
tokens[nr_token].type=262;
strncpy(tokens[nr_token].str,&e[position-substr_len],substr_len);
break;
case 263:
tokens[nr_token].type=263;
strncpy(tokens[nr_token].str,&e[position-substr_len],substr_len);
break;
case 265:
tokens[nr_token].type=265;
strncpy(tokens[nr_token].str,&e[position-substr_len],substr_len);
break;
default:
nr_token--;
break;
}
nr_token++;
break;
}
}
if (i == NR_REGEX) {
printf("no match at position %d\n%s\n%*.s^\n", position, e, position, "");
return false;
}
}
nr_token--;
return true;
}
递归求值
- 检查左右括号是否匹配。
在该函数中,设置了两个变量left=0,flag=0,若tokens[p]为左括号,则判断从tokens[p+1]到tokens[q]。
遇到了左括号则left++;
遇到右括号则left--,且判断left是否等于0且当前位置是否到了末尾,若left为0且当前位置不在末位,flag赋值1,说明两侧括号不匹配,若left小于0则assert(0),因为说明出现了讲义中提到的类似(4+3))*((2+1)的情况。最后若(left==0)&&(tokens[q]为) )&&flag!=1,即该表达式仅有一对括号,位于两端,互相匹配,则返回1;若left!=0则assert(0),说明可能出现了不匹配的括号;其他情况都返回0;
结果截图:
代码如下:
- 找出dominant operator。
其实做完之后发现自己用的方法太暴力太傻了……完全可以在rules中再设置一个变量用来记录运算符优先级,方便简单,但是已经做完了暂时不改了,等空的时候改过来。
思路就是不考虑十进制十六进制寄存器和非,将op值设为起始位置(若表达式为!2,则返回op为!的位置),然后判断当前位置的运算符,(若遇到左括号,用r来记录括号的对数,然后从左右括号包含的范围之后的一位再判断运算符优先级,跳过括号内的运算符),与op位置的运算符比较优先级,优先级小于等于op位置,则op=当前位置。其中,-和*需要再判断它是否是第一个位置或者前面一位是否为符号,右括号除外,为了避免将指针和负号错认。
代码如下:
- 递归求值。
eval(p,q)函数大体上就是先判断表达式的首尾地址是否合理,不合理assert(0);再判断pq是否相等,若相等它最终必然是一个数值并返回它的值;然后运用check_parentheses函数判断该表达式是否被一对匹配的括号包围着,若是则递归求值括号包围的那个表达式。若以上判断都是否,则用find_dominant_operator函数找出最后一步运行的运算符所在位置op,而后递归调用eval函数,求出op左右两端表达式的值val1,val2,再根据op的运算符进行对应的操作并返回结果。
4)实现算术表达式的递归求值。
其中提到了要区分出(4+3))*((2+1)和(4+3)*(2-1),其实在check_parentheses函数中已经实现了,上文已经提到思路。
5)实现带有负数的算术表达式的求值(选做)。
1.负号和减号如何区分?
负号可以在第一位,或者它前面一位是运算符,)除外。而减号不是如此。
2.负号是单目运算符,分裂时需注意什么?
不要和双目运算符减号搞混。与前一运算符分裂,与其后的一个数值或变量或寄存器之后的运算符分裂。
调试中的表达式求值
- 扩展功能
需要实现十进制、十六进制、寄存器、左右括号,+-*/,==,!=,与或非,指针解引用。其中,+-*/、左右括号、十进制已经在上文中实现。==,!=,&&,||,同+类似。其余的功能实现的方法在代码贴图中解释了。
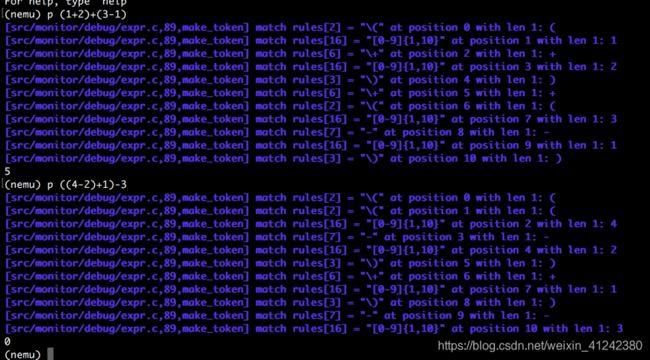
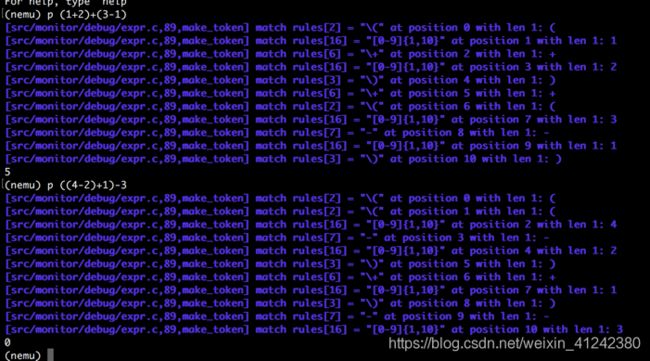
结果截图:
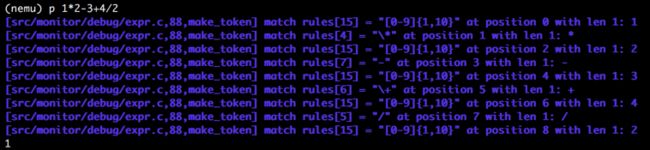
加减乘除
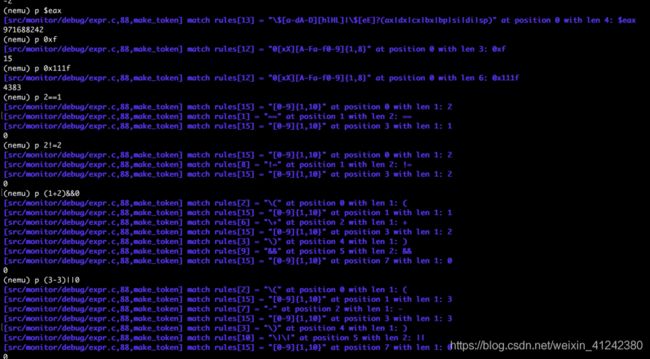
负号
寄存器、十六进制、==、!=、&&、||
括号
代码如下:
在ui.c函数中cmd_p: