单词争霸

题意
给n个单词，现在A和B进行博弈，A先手
轮流取一个单词，满足这个单词不为之前取过的某个单词的前缀
问A是否能赢，第一个取得单词可以是那些
读入按字典序给

样例
input:
5 9
ac
car
care
careful
carefully

output:
careful

串总长1e5 1s

---

假装建ac自动机
将每个串向读入中的最长前缀认爸爸
形成一个森林
博弈内容变为每次删掉一个点到根的路径，儿子分开，不能删者输

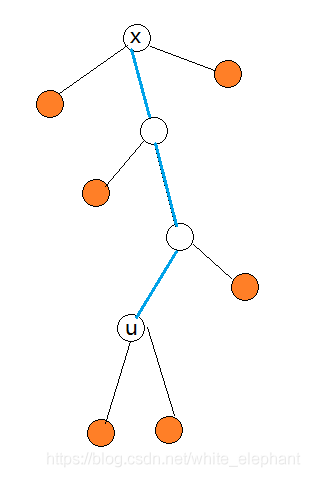
用SG函数，对x的子树进行博弈胜负状态用$SG(x)$表示，$SG(\varnothing )=1$
只对一棵树考虑，删掉一个点到根路径，子状态一定是若干棵树
记$anc(u)$为u与u的所有祖先，删掉$anc(u)$所有点。
裂成的子树的根集合是$sep(u)=\{b|fa(b)=a,a\in anc(u),b̸\in anc(u)\}$
这个子状态的SG函数就是$SG(sep(u))={⨁}_{v\in sep(u)}SG(v)$
那么一棵树x的SG值可以用下式求$SG(x)=mex\{SG(u)|u\in subtree(x)\}$

(橙点为sep(u))

因此，我们用字典树$trie(x)$记下所有$se{p}_x(u)$
初始情况下，trie(x)只有儿子的SG的异或
记$xor(x)={⨁}_{fa(u)=x}SG(u)$
那么${\forall }_{s\in trie(x)},s⨁xor(x)⨁SG(u)\in trie(fa(x))$
就是说每往上走，就将trie里每个数异或上fa(x)除x之外的所有儿子SG值的异或，然后将trie合并到fa(x)上
SG(x)可以通过trie来求mex

合并不用启发式，可以参照线段树合并，如果在两棵树中，某个点都存在，就走下去合并，否则就只保留其中一棵，时间复杂度同线段树合并$O(\sum size\log (\sum size))$

#include
#include
#include
#define N 100100
#define M 2000100
using namespace std;
int n,m,len[N],tag[M],sz[M],cnt,sn[M][2],nx[120],fir[N],nex[N],to[N],top,que[N],t,sg[N],p[N],pxr[N],q[N],rt[N];
char c[120],s[120],S[N][110];
#define link(u,v) to[++top]=v,nex[top]=fir[u],fir[u]=top
void Xor(int x,int v){
	if(!x)return;
	tag[x]^=v;
}
void down(int x,int f){
	if(!x)return;
	if(tag[x]){
		int T=tag[x]&1<<f;
		if(T)swap(sn[x][0],sn[x][1]);
		Xor(sn[x][0],tag[x]-T);
		Xor(sn[x][1],tag[x]-T);
		tag[x]=0;
	}
}
void ins(int &x,int f,int v){
	if(!x)x=++cnt;
	if(f<0){sz[x]=1;return;}
	down(x,f);
	int w=(v&1<<f)>>f;
	ins(sn[x][w],f-1,v);
	sz[x]=sz[sn[x][0]]+sz[sn[x][1]];
}
void merge(int &u,int v,int f){
	if(!u||!v){u=u+v;return;}
	if(f<0){sz[u]=1;return;}
	down(u,f);down(v,f);
	merge(sn[u][0],sn[v][0],f-1);
	merge(sn[u][1],sn[v][1],f-1);
	sz[u]=sz[sn[u][0]]+sz[sn[u][1]];
}
int mex(int x,int f){
	if(!x)return 0;
	down(x,f);
	if(sz[sn[x][0]]<1<<f)return mex(sn[x][0],f-1);
	return mex(sn[x][1],f-1)^1<<f;
}
int main(){
	scanf("%d %d",&n,&m);
	for(int i=1;i<=n;++i){
		char ch;int P=0,l=0;
		for(;(ch=getchar())>'z'||ch<'a';);
		for(;(ch>='a'&&ch<='z')||(ch>='0'&&ch<='9');ch=getchar()){
			++l;S[i][l]=s[l]=ch;
			if(l==P+1&&ch==c[l])P=l;
		}if(nx[P])link(nx[P],i);else que[++t]=i,p[i]=1;
		for(int j=P+1;j<=l;++j)nx[j]=nx[j-1],c[j]=s[j];nx[l]=i;
		len[i]=l;c[l+1]=0;
	}
	for(int i=1;i<=t;++i)
		for(int x=que[i],o=fir[x];o;o=nex[o])que[++t]=to[o];
	for(int i=t;i;--i){
		int x=que[i],xr=0;
		for(int o=fir[x];o;o=nex[o])xr^=sg[to[o]];
		ins(rt[x],16,xr);
		for(int o=fir[x];o;o=nex[o]){
			Xor(rt[to[o]],xr^sg[to[o]]);
			merge(rt[x],rt[to[o]],16);
		}sg[x]=mex(rt[x],16);
	}int Xr=0;
	for(int i=1;i<=n;++i)if(p[i])Xr^=sg[i];
	if(!Xr)printf("Can't win at all!!");else{
		int CNT=0;
		for(int i=1;i<=n;++i)if(p[i]){
			que[t=1]=i;pxr[1]=0;
			for(int j=1;j<=t;++j){
				int x=que[j],xr=0;
				for(int o=fir[x];o;o=nex[o])xr^=sg[to[o]];
				if((pxr[j]^xr^sg[i]^Xr)==0)q[x]=1;
				for(int o=fir[x];o;o=nex[o])que[++t]=to[o],pxr[t]=pxr[j]^xr^sg[to[o]];
			}
		}
		for(int i=1;i<=n;++i)if(q[i]){
			for(int j=1;j<=len[i];++j){
				++CNT;putchar(S[i][j]);
				if(CNT==50)putchar('\n'),CNT=0;
			}
		}
	}
}