PAT 1021 Deepest Root (25分) 从测试点3超时到满分再到代码优化

题目

A graph which is connected and acyclic can be considered a tree. The height of the tree depends on the selected root. Now you are supposed to find the root that results in a highest tree. Such a root is called the deepest root.

Input Specification:
Each input file contains one test case. For each case, the first line contains a positive integer N (≤10⁴​​ ) which is the number of nodes, and hence the nodes are numbered from 1 to N. Then N−1 lines follow, each describes an edge by given the two adjacent nodes’ numbers.

Output Specification:
For each test case, print each of the deepest roots in a line. If such a root is not unique, print them in increasing order of their numbers. In case that the given graph is not a tree, print Error: K components where K is the number of connected components in the graph.

Sample Input 1:
5
1 2
1 3
1 4
2 5
Sample Output 1:
3
4
5
Sample Input 2:
5
1 3
1 4
2 5
3 4
Sample Output 2:
Error: 2 components

题目解读

给出一个无向图的N个节点和N-1条边，问其能否形成一棵树，如果不可以，请输出
“Error: %d components”，其中这个%d指的是这个图的连通分量个数；如果可以形成树，那请问，哪个节点作为树根，这棵树将会有最大的高度？如果多个节点都能达到这个要求，将这些节点按顺序输出。

关于图的连通分量，一般都会采用并查集或者DFS来进行判断，我们这里选择用DFS，因为这个思路真的简单

思路一（测试点3超时）

1. dfs(i) 判断连通分量的个数：
   用一个visit数组记录节点的访问状况，初始化为false，dfs内把和i直接关联或间接关联的节点都标记为true，这样，就相当于一个连通分量从整个节点集中排除出去了，我们需要统计dfs执行了多少次才使得visit数组全为false，就能得到连通分量的个数。
2. 让每个节点都作为根节点，利用dfs(i, deep, deepest)函数去求得这棵树的最大深度，并用一个全局的maxheight记录全局最优，如果它更大（deepest>maxheight），那就把之前保存的根的集合roots清空，把它加进去；如果它作为根得到的deepest==maxnheight，那就把它直接加入roots。
3. 看看代码吧，注释已经不能再详细了。

#include 
#include 
#include 
using namespace std;

// n个节点
int n;
// 邻接矩阵，下标从1开始，最终造成内存溢出，测试点3结果是超时，内存占用显示0
bool edge[10001][10001];
// 能使得高度最大的全部节点
vector<int> maxheight_roots;
// 最大高度
int maxheight;

bool visit[10001];
// 用于 深度优先搜索判断它有几个连通分量，
// 每进行一次dfs,就划分出一个连通分量，visit集合中这部分节点都变成true
// 判断 执行了几次 dfs才使得visit全为true，就知道有几个连通分量，如果连通分量大于1，那么就不是一棵树
void dfs(int s) {

    visit[s] = true;
    for (int j = 1; j <= n; ++j) {
        // 和他直接或间接相连的点全标为true
        if (edge[s][j] && !visit[j])
            dfs(j);
    }
}
// 用于求得 以每个节点作为根节点，能得到的最大高度
// deepest保存这个结果，注意这个引用传值，相当于c语言中的指针，能改变这个值
// deep 当前节点s在第几层
// 其实上面那个函数没必要创建，用这个就可以了，只是为了让大家看清楚我的思路
void dfs(int s, int deep, int &deepest) {
    // 更新 最大高度
    if (deep > deepest) {
        deepest = deep;
    }

    visit[s] = true;

    for (int j = 1; j <= n; ++j) {
        // 和它直接相连的，相当于全是它的孩子，全在它的下一层
        if (edge[s][j] && !visit[j]) {
            dfs(j, deep + 1, deepest);
        }
    }
}

int main() {

    cin >> n;

    int f, t;
    // n个节点n-1条边
    for (int i = 1; i < n; ++i) {
        cin >> f >> t;
        // 构建邻接矩阵
        edge[f][t] = edge[t][f] = true;
    }
    // 统计连通分量的个数
    int cnt = 0;
    for (int i = 1; i <= n; ++i) {
        if (!visit[i]) {
            // 每进行一次dfs,就划分出一个连通分量，visit集合中这部分节点都变成true
            dfs(i);
            cnt++;
        }
    }
    // 超过一个连通分量，不能构成树
    if (cnt > 1) {
        printf("Error: %d components", cnt);
        return 0;
    }
    // 以每个节点为根节点，得到它形成的树的最大高度
    for (int i = 1; i <= n; ++i) {
        fill(visit, visit + n + 1, false);
        // 保存以i为根的树的最大高度
        int deepest = 0;
        // 根节点是第一层，因为是引用传值，执行完后deepest改变
        dfs(i, 1, deepest);
        // 如果这棵树的最大高度大于全局保存的最大高度
        if (deepest > maxheight) {
            // 更新最大高度
            maxheight = deepest;
            maxheight_roots.clear();
            // 只把它做为根节点
            maxheight_roots.push_back(i);
        // 这棵树的最大高度和全局最大高度相等，说明它也是一个符合要求的根节点
        } else if (deepest == maxheight) {
            // 加进来
            maxheight_roots.push_back(i);
        }
    }
    // 输出所有合法的根节点即可
    for (auto it : maxheight_roots)
        cout << it << endl;

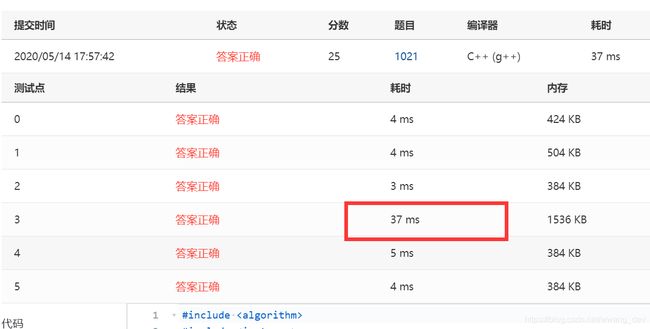
    return 0;
}

最终结果是 测试点3超时了

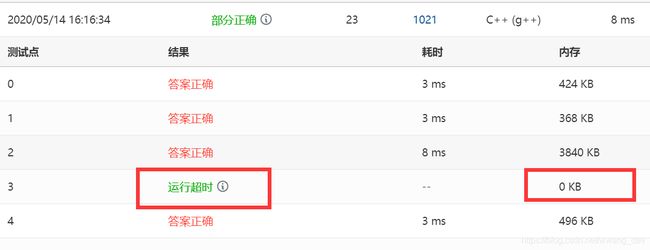
可以很明显看出来是内存溢出！！！！（内存显示的是0啊），为啥呢？树 是稀疏图，用邻接矩阵去存太浪费空间了。

思路二（满分通过，但运行时间太长）

既然知道问题在哪，那么就好办了，我们只需要把邻接矩阵改为邻接表进行存储就好了，我们用可变数组vector。

#include 
#include 
#include 
#include 
using namespace std;

// n个节点
int n;
// // 邻接矩阵，下标从1开始
// bool graph[10001][10001];
// 邻接表，改成邻接表后测试点3通过，但是运行时间1131ms
vector<vector<int>> graph;
// 
vector<bool> visit;

// 能使得高度最大的全部节点
vector<int> maxheight_roots;
// 最大高度
int maxheight;


// 用于求得 以每个节点作为根节点，能得到的最大高度
// deepest保存这个结果，注意这个引用传值，相当于c语言中的指针，能改变这个值
// deep 当前节点s在第几层
// 其实上面那个函数没必要创建，用这个就可以了，只是为了让大家看清楚我的思路
void dfs(int i, int deep, int &deepest) {
    // 更新 最大高度
    if (deep > deepest) {
        deepest = deep;
    }
    // 如果忽略上面那几行代码和后两个参数，就是用来 深度优先搜索判断它有几个连通分量，
    // 每进行一次dfs,就划分出一个连通分量，visit集合中这部分节点都变成true
    // 判断 执行了几次
    // dfs才使得visit全为true，就知道有几个连通分量，如果连通分量大于1，那么就不是一棵树

    visit[i] = true;

    for (int j = 0; j < graph[i].size(); ++j) {
        // 和它直接相连的，相当于全是它的孩子，全在它的下一层
        // 注意换成邻接表后的写法
        if (!visit[graph[i][j]]) {
            dfs(graph[i][j], deep + 1, deepest);
        }
    }
}

int main() {

    cin >> n;

    graph.resize(n + 1);
    visit.resize(n + 1);

    int f, t;
    // n个节点n-1条边
    for (int i = 1; i < n; ++i) {
        cin >> f >> t;
        // 构建邻接表
        graph[f].push_back(t);
        graph[t].push_back(f);
    }
    // 统计连通分量的个数
    int cnt = 0, any = 0;
    for (int i = 1; i <= n; ++i) {
        if (!visit[i]) {
            // 每进行一次dfs,就划分出一个连通分量，visit集合中这部分节点都变成true
            dfs(i, 0, any);
            cnt++;
        }
    }
    // 超过一个连通分量，不能构成树
    if (cnt > 1) {
        printf("Error: %d components", cnt);
        return 0;
    }
    // 以每个节点为根节点，得到它形成的树的最大高度
    for (int i = 1; i <= n; ++i) {
        fill(visit.begin(), visit.end(), false);
        // 保存以i为根的树的最大高度
        int deepest = 0;
        // 根节点是第一层，因为是引用传值，执行完后deepest改变
        dfs(i, 1, deepest);
        // 如果这棵树的最大高度大于全局保存的最大高度
        if (deepest > maxheight) {
            // 更新最大高度
            maxheight = deepest;
            maxheight_roots.clear();
            // 只把它做为根节点
            maxheight_roots.push_back(i);
            // 这棵树的最大高度和全局最大高度相等，说明它也是一个符合要求的根节点
        } else if (deepest == maxheight) {
            // 加进来
            maxheight_roots.push_back(i);
        }
    }
    // 输出所有合法的根节点即可
    for (auto it : maxheight_roots)
        cout << it << endl;

    return 0;
}

看看结果吧

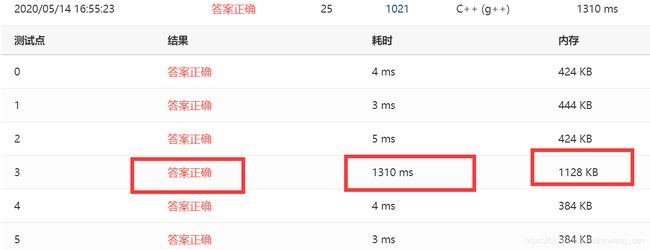
1310ms，扎心了老铁，why??? why??? 不能怪我没有优化，因为我不会！！！

最终版本

不参考各路大神的代码，我怎么可能会优化呢？天真！！，果然，各路大神都是这么干的，果然不是我能想到的：

1. 从任意一个节点开始进行深度优先遍历，找到离他最远的所有节点（可能不止一个，记为集合A）；
2. 再从A中任意选一个节点出发进行深度优先遍历，找到离他最远的节点（记为集合B），
3. 最后最深根就是这两个集合的并集。

为啥呢？？其实我自己拿纸画了画，大概是能明白的，但我可能说不清楚，所以我在这里把牛客网的链接贴出来大家自己去看看，说的挺清楚的。（牛客网解释）

不过为了防止链接以后失效了，我在这里把最好的两个解释直接贴出来吧。

解释一：

这个算法有一个很玄奥的地方，就是两次遍历都有帅气逼人地用到了任取一词，为了说明算法的正确性，让我先上一张图

就是上面这幅图，圆的是顶点，长的是边，中间蓝色加省略号是省略省略不提的部分，然后红色是主干，也就是最长路，绿色是侧枝。

很容易理解对于任何一条侧枝 DE,存在|DE| < min(|AD|，|DC|),现在分类讨论：

1. 对于第一次DFS选择的起点，如果是红色路径上的点，第一次DFS得到的最长路必定是距离较远的最长路顶点，在这幅图中就是说要么是A，要么是C，同时可以看到，假如起点是B，我们在DFS的时候E点的DFS深度也会是最长路径，也就是说我们选出了最起码一侧的所有最长路的端点。
2. 如果第一次选择的起点是侧枝上的点，如F （侧枝上还有侧枝的情况请自行脑补） ，F在进行DFS搜索的时候必定会经过D点，那么问题已经转化成了第一题的问题。
   至于第二次DFS应该很好理解既然第一次选出了一端的所有顶点，第二次肯定会选出另一端所有顶点。
   
   至此该问题圆满解决。

解释二：

从任意一个节点开始进行深度优先遍历，找到离他最远的节点（可能不止一个，记为集合A）；第二步：再从A中任意选一个节点出发进行深度优先遍历，找到离他最远的节点（记为集合B），最后最深根就是这两个集合的并集。

证明：第一步找出的节点一定是全局的最深根。

1 根据全局最优解一定是局部最优解的原理：最后全局的最深根一定也是某个局部最优解，比如：因为全局最深的根是固定的，不失一般性，我们就把他们标为1、2、3、4、5，那么从图中中任意一点出发，例如A，从他出发找到的局部最优解一定是在1、2、3、4、5，反之，如不在，也就是说有比1、2、3、4、5更深的节点，我们假设它存在并且成为B,那么可想而知，从1到B肯定要比从1到2要深，这就与1、2、3、4、5是全局最优解矛盾，所以假设不成立。原命题成立。即局部最优解一定在1、2、3、4、5中。

2 由第一步知道局部最优解是固定的，且全局最优解是局部最优解，根据这两条结论，得出：第一次遍历得到的最深的节点就是最深根

由于从最深根出发到最深的叶子节点是相互对称的，所以我们再从当前的最深根出发遍历一次得到其他的最深根，然后做一次去重即可。

下面贴上我自己的写的代码吧，参考了柳神的代码，然后自己省去了一些小瑕疵，注释还是日常详细详细再详细，给你最好的阅读体验，哈哈哈。

#include 
#include 
#include 
#include 
using namespace std;

/**
 * 牛客网解释：https://www.nowcoder.com/questionTerminal/f793ad2e0c7344efa8b6c18d10d4b67b
 * 1.
 * 从任意一个节点开始进行深度优先遍历，找到离他最远的节点（可能不止一个，记为集合A）；
 * 2.
 * 再从A中任意选一个节点出发进行深度优先遍历，找到离他最远的节点（记为集合B），
 * 3. 最后最深根就是这两个集合的并集。
 */

// n个节点
int n;

// 邻接表，下标全从0开始，
vector<vector<int>> graph;
// 下标从0开始
vector<bool> visit;

// 保存dfs时，得到的最深层节点
vector<int> temp_roots;

// 最大高度
int maxheight;

// 用于求得 以每个节点作为根节点，能得到的最大高度
// deepest保存这个结果，注意这个引用传值，相当于c语言中的指针，能改变这个值
// deep 当前节点s在第几层
// 其实上面那个函数没必要创建，用这个就可以了，只是为了让大家看清楚我的思路
void dfs(int i, int deep) {
    // 更新 最大高度
    if (deep > maxheight) {
        // 更新最大高度
        maxheight = deep;
        temp_roots.clear();
        // 只把它做为根节点
        temp_roots.push_back(i);
        // 这棵树的最大高度和全局最大高度相等，说明它也是一个符合要求的根节点
    } else if (deep == maxheight) {
        // 加进来
        temp_roots.push_back(i);
    }
    // 如果忽略上面那几行代码和后两个参数，就是用来
    // 深度优先搜索判断它有几个连通分量，
    // 每进行一次dfs,就划分出一个连通分量，visit集合中这部分节点都变成true
    // 判断 执行了几次
    // dfs才使得visit全为true，就知道有几个连通分量，如果连通分量大于1，那么就不是一棵树

    visit[i] = true;

    for (int j = 0; j < graph[i].size(); ++j) {
        // 和它直接相连的，相当于全是它的孩子，全在它的下一层
        // 注意换成邻接表后的写法
        if (!visit[graph[i][j]]) {
            dfs(graph[i][j], deep + 1);
        }
    }
}

int main() {

    cin >> n;

    graph.resize(n + 1);
    visit.resize(n + 1);

    int f, t;
    // n个节点n-1条边
    for (int i = 1; i < n; ++i) {
        cin >> f >> t;
        // 构建邻接表
        graph[f].push_back(t);
        graph[t].push_back(f);
    }
    // 统计连通分量的个数
    int cnt = 0;
    for (int i = 1; i <= n; ++i) {
        if (!visit[i]) {
            // 每进行一次dfs,就划分出一个连通分量，visit集合中这部分节点都变成true
            dfs(i, 1);
            cnt++;
        }
    }
    // 超过一个连通分量，不能构成树
    if (cnt > 1) {
        printf("Error: %d components", cnt);
        return 0;
    }
    // 从第一次dfs得到的集合temp_roots拿出一个根，再进行一次dfs，得到集合B
    // 集合取交集就是结果，多个根的话，还要按大小火顺序保存，我们借助一个set
    set<int> roots;
    // 先把集合A转移进来，
    for (auto it : temp_roots)
        roots.insert(it);
    // 清空temp_roots以保存集合B
    temp_roots.clear();
    // 清空visit
    fill(visit.begin(), visit.end(), false);
    // 再以集合A中任意一个元素作为根去dfs
    dfs(*roots.begin(), 1);
    // 再把集合B转移进来，相当于取了并集，set自动去重排序
    for (auto it : temp_roots)
        roots.insert(it);
    
    // 输出所有合法的根节点即可
    for (auto it : roots)
        cout << it << endl;

    return 0;
}

再看看结果

这下子就满意多了，^_^