leetcode1044. 最长重复子串 (Rabin-Karp + 二分 )

leetcode1044. 最长重复子串

题意

给出一个字符串 S，考虑其所有重复子串（S 的连续子串，出现两次或多次，可能会有重叠）。

返回任何具有最长可能长度的重复子串。（如果 S 不含重复子串，那么答案为 “”。）

思路

这里两个相同子串的最大长度满足递增性， 所以可以用二分的枚举这个长度值m。

那么问题就变成在一个字符串里枚举是否有两个长度为m的相同子串。

枚举过程，我们可以想象是就是一个大小为m的窗口滑动的过程。 总的时间复杂度是 滑动过程乘以比较窗口内字符串是否出现 O(len(S)*len(S))。

在这里新学习Rabin-Karp算法可以实现，O(1)计算出窗口内字符串的hash值，从而判断是否出现过。

具体的Rabin-Karp算法就是将一个字符串用公式计算成唯一的hash数值,原理很简单。

计算公式如下：

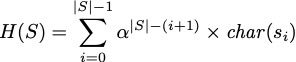
其中a是每个字符串单个字符的种类，这样就能保证每个字符串hash值是唯一的，比如全是小写字母的字符串,a可以是26。

当窗口滑动时，新的字符串hash计算公式也很简单，如下：

代码

class Solution:
    def rabin_karp_check(self, nums, a ,m, n) :
        p = pow(a , m-1, self.mod)
        import functools
        cur = functools.reduce(lambda x,y: (x*a+y) % self.mod, nums[:m])
        seed = {cur}
        for index in range(m, n):
            cur = ((cur - p * nums[index-m])* a + nums[index])%self.mod
            if cur in seed :
                return index - m +1
            seed.add(cur)
        return -1

    def longestDupSubstring(self, S: str) -> str:
        self.mod = 2**63 -1
        l , r = 1, len(S)
        nums = [ord(c) - ord('a') for c in S]  #把字符映射为数值
        pos = 0
        while l <=r :
            mid = int((l+r) /2)
            index = self.rabin_karp_check(nums, 26, mid, len(S))
            if index != -1:
                l= mid + 1
                pos = index
            else : r = mid - 1
        return S[pos: pos +l-1]

这题补充了functools.reduce()的用法。

另外注意这题数据量很大,我用c++写的版本，mod 取到最大还是hash后还是会冲突，过不了。

Wrong的代码先贴在这，有时间再纠结怎么改对…

class Solution {
public:
    int rabin_karp_check(vectornums, long long  a, int m, int n){
        set cot;
        long long cur = 0, mod = 6*(1<<20)+1;
        long long p =1;
        for(int i=0;i0){
                return i-m+1;
            }
            else{
                cot.insert(cur);
            }
        }
        return -1;
    }

    string longestDupSubstring(string S) {
         int l =1 ,r= S.length();
         vector nums;
         for(char c:S){
            nums.push_back(c - 'a');
         }
         int res =0;
         while(l<=r){
            int mid = (l+r) *0.5;
            int index = rabin_karp_check(nums, 26, mid, S.length());
            if(index != -1){
                res = index;
                l = mid +1;
            }
            else{
                r= mid - 1;
            }
         }
         return S.substr(res, res+l-1);
    }
};