2016腾讯校招研发笔试(三)
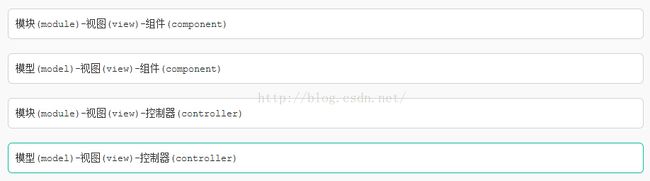
1.我们常说的mvc框架是指的什么的?
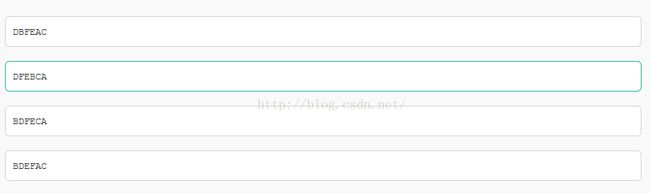
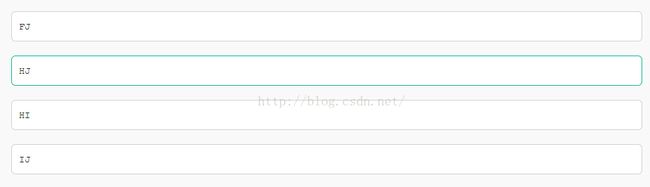
2.对某二叉树进行先序遍历的结果是ABDEFC,中序遍历的结果是DBFEAC,则后序遍历的结果是()
3.
|
1
2
3
4
5
6
|
struct
A{
long
a1;
short
a2;
int
a3;
int
*a4;
};
|
64位下int为4字节,long和指针为8字节,参看:http://blog.csdn.net/zhangjikuan/article/details/46661047
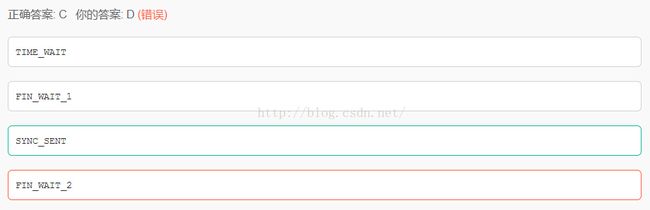
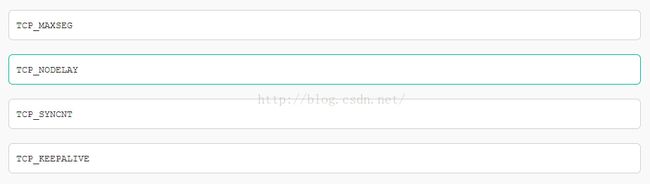
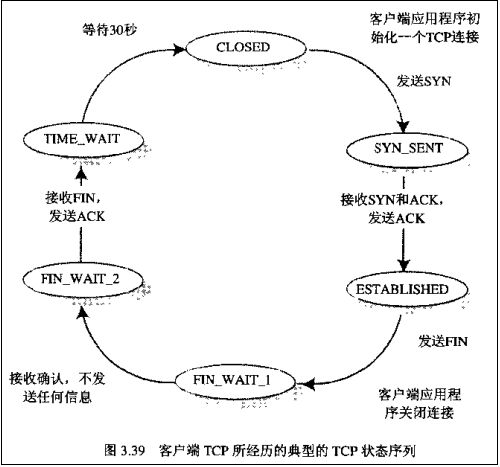
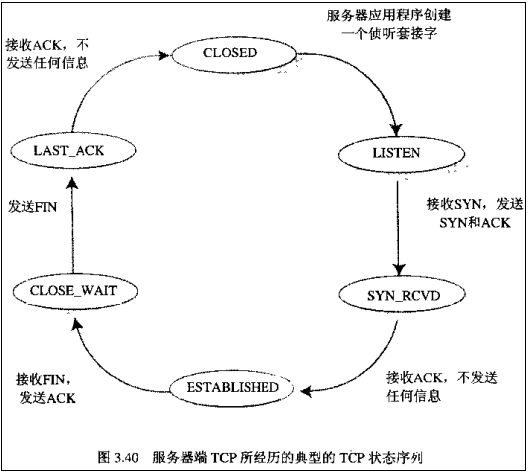
4.以下不属于tcp连接断开的状态是?
TCP连接断开的状态包括:FIN-WAIT-1(服务器端主动关闭TCP,等待客户端发送ACK时服务器端的状态)、
CLOSE-WAIT、
FIN-WAIT-2(服务器端收到ACK后的状态)、
LASR-ACK、
TIME-WAIT(只要一方处于此状态,连接不能再用)、
CLOSE
5.下面关于ICMP协议的描述中,正确的是()
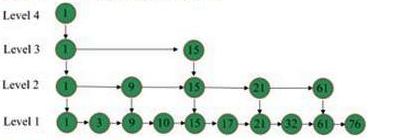
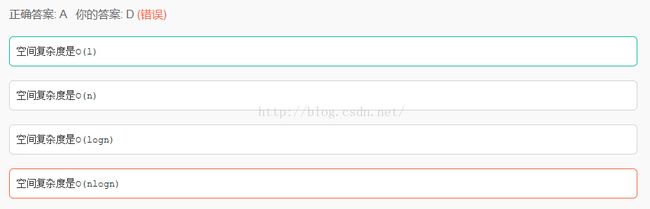
6.有如下一个类似跳表的数据结构:每层都是已经排好序的链表,level1层的链表有所有元素,levelN层的链表只有levelN-1的1半的元素,levelN层的结点指向levelN-1层中相同的结点。请问查找一个元素的时间复杂度是:
8.C语言里i=5,j=7,请问i|j等于多少?
9.
|
1
2
3
4
5
6
7
8
9
|
int
main(
int
argc,
char
*argv[])
{
int
a=10;
int
b=4;
int
c=a/b;
int
d=c*a*b++;
std:cout<
return
0;
}
|
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
|
#include
#include
union
X
{
int32_t a;
struct
{
int16_t b;
int16_t c;
};
};
int
main(){
X x;
x.a=0x20150810;
printf
(
"%x,%x\n"
,x.b,x.c);
return
0;
}
|
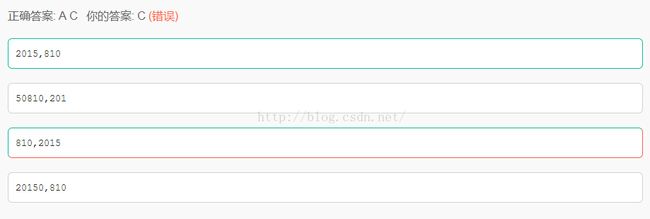
要考虑大小端两种情况,
union:内部数据结构占用相同内存,即int_32t和struct占用同一块内存区域,所以向a中赋值相当于是向bc中
大端:高字节放低字节:c为高字节放0810,b低字节放2015
小端:高字节放高字节:c为高字节,放2015,b低字节放0810
11.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
|
#include
using
namespace
std;
int
i=1;
class
MyCls{
public
:
MyCls():m_nFor(m_nThd),m_nSec(i++),m_nFir(i++),m_nThd(i++){
m_nThd=i;
}
void
echo(){
cout<<
"result:"
<
}
private
:
int
m_nFir;
int
m_nSec;
int
m_nThd;
int
&m_nFor;
};
int
main()
{
MyCls oCls;
oCls.echo();
return
0;
}
|
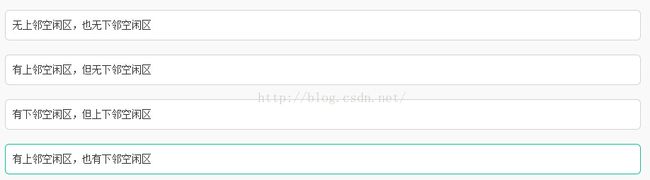
- 有上邻空闲区,但无下邻空闲区.只修改上邻空闲区长度(为收回的空闲区长度与原上邻区长度之和),空闲区数不变
- 无下邻空闲区,但有下邻空闲区.改记录这个下邻空闲区记录的地址为收回空闲区的地址,长度为下邻空闲区的长度和收回空闲区的长度,空闲区数不变
- 有上邻空闲区,也有下邻空闲区.改记录上邻区记录的长度(为上邻区长度、下邻区长度和收回区长度之和),再把下邻区记录的标志位改为空,即空闲区数-1
- 无上邻空闲区,也无下邻空闲区.那么找一个标志位为空的记录,记下该回收区的起始地址和长度,且改写相应的标志位为未分配,表明该登记栏中指示了一个空闲区。 空闲区数+1
这个算法最明显的有两种解法,
1.每次进来一个变量n,就遍历前面n个数,然后求和,再取平均,这样的话时间复杂度为O(n),空间为O(1);
2.以空间换时间:从前往后没计算一次保留一次求和值到一个辅助空间,这样计算下一个的时候直接取得前一个和值加上当前数,再取平均得到当前平均,这样的话时间复杂度为O(1),空间为O(n)
先序遍历顺序是:M-L-R;
后序遍历顺序是:L-R-M;
所以只有A对了。
|
1
2
3
4
5
6
|
int
intValue=1024;
char
str[]=
"Tencent"
;
const
char
* ch=str;
sizeof
(intValue)=__a___;
sizeof
(str)=__b____;
sizeof
(ch)=____c___;
|
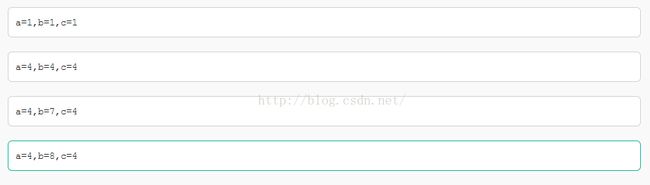
正确答案: A 你的答案: B (错误)
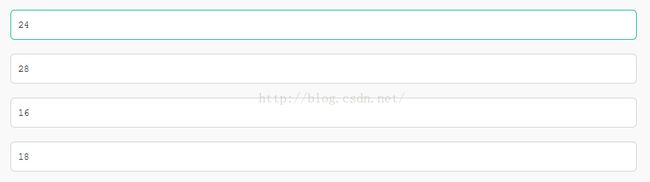
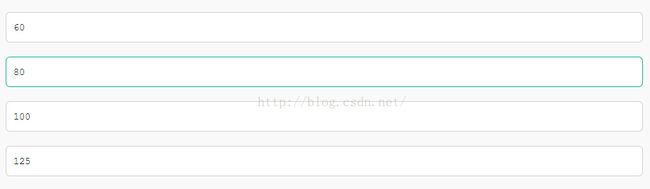
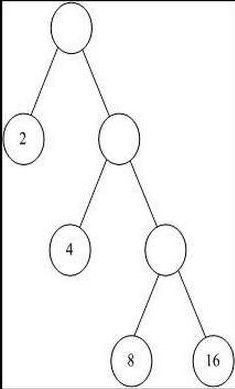
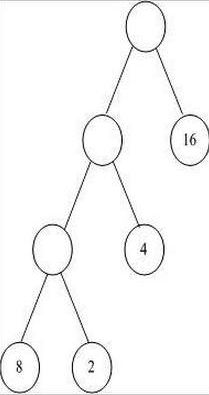
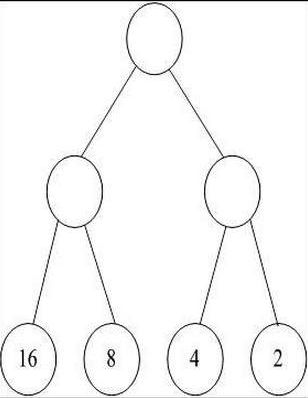
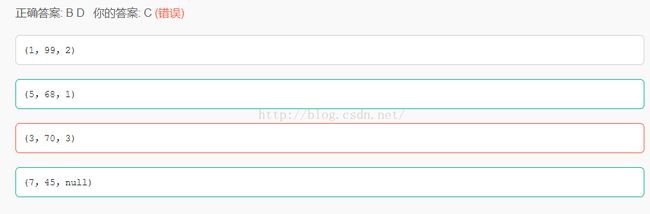
最优二叉树,是指WPL(带权路径长度之和)最小WPL(A):16*1+8*2+2*3+3*4=50
WPL(B):2*1+4*2+8*3+16*3=82
WPL(C):16*1+4*2+8*3+2*3=54
WPL(D):16*2+8*2+4*2+2*2=60
所以选A
1 好处 及 用途
红黑树 并不追求“完全平衡 ”——它只要求部分地达到平衡要求,降低了对旋转的要求,从而提高了性能。
红黑树能够以 O(log2 n) 的时间复杂度进行搜索、插入、删除操作。此外,由于它的设计,任何不平衡都会在三次旋转之内解决。当然,还有一些更好的,但实现起来更复杂的数据结构 能够做到一步旋转之内达到平衡,但红黑树能够给我们一个比较“便宜”的解决方案。红黑树的算法时间复杂度和AVL相同,但统计性能比AVL树更高。
当然,红黑树并不适应所有应用树的领域。如果数据基本上是静态的,那么让他们待在他们能够插入,并且不影响平衡的地方会具有更好的性能。如果数据完全是静态的,例如,做一个哈希表,性能可能会更好一些。
在实际的系统中,例如,需要使用动态规则的防火墙系统,使用红黑树而不是散列表被实践证明具有更好的伸缩性。
典型的用途是实现关联数组
2 AVL树是最先发明的自平衡二叉查 找树。在AVL树中任何节点的两个儿子子树的高度最大差别为一,所以它也被称为高度平衡树。查找、插入和删除在平均和最坏情况下都是O(log n)。增加和删除可能需要通过一次或多次树旋转来重新平衡这个树。AVL树得名于它的发明者 G.M. Adelson-Velsky 和 E.M. Landis,他们在 1962 年的论文 "An algorithm for the organization of information" 中发表了它。
引入二叉树的目的是为了提高二叉树的搜索的效率,减少树的平均搜索长度.为此,就必须每向二叉树插入一个结点时调整树的结构,使得二叉树搜索保持平衡,从而可能降低树的高度,减少的平均树的搜索长度.
AVL树的定义:
一棵AVL树满足以下的条件:
1>它的左子树和右子树都是AVL树
2>左子树和右子树的高度差不能超过1
从条件1可能看出是个递归定义,如GNU一样.
性质:
1>一棵n个结点的AVL树的其高度保持在0(log2(n)),不会超过3/2log2(n+1)
2>一棵n个结点的AVL树的平均搜索长度保持在0(log2(n)).
3>一棵n个结点的AVL树删除一个结点做平衡化旋转所需要的时间为0(log2(n)).
从1这点来看 红黑树是牺牲了严格的高度平衡的优越条件 为 代价红黑树能够以O(log2 n)的时间复杂度进行搜索、插入、删除操作。此外,由于它的设计,任何不平衡都会在三次旋转之内解决。当然,还有一些更好的,但实现起来更复杂的数据结构 能够做到一步旋转之内达到平衡,但红黑树能够给我们一个比较“便宜”的解决方案。红黑树的算法时间复杂度和AVL相同,但统计性能比AVL树更高.
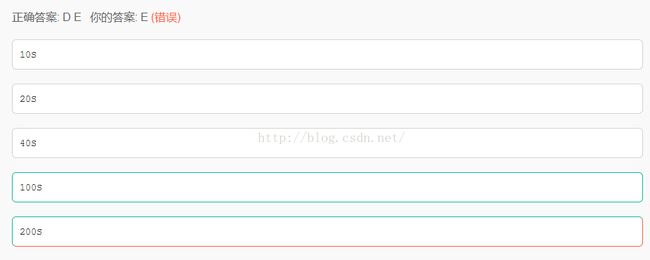
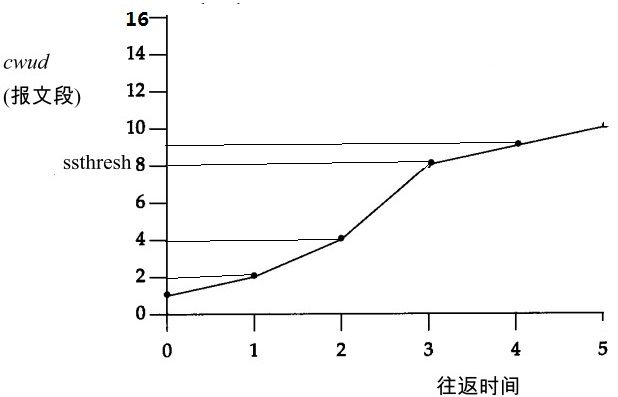
2RTT 结束,2KB->4KB
3RTT 结束,4KB->8KB(到达阈值,执行拥塞避免算法)
4RTT 结束,8KB->9KB
结果C
说说C吧,也是基本的,浮点型(double,flout)由于是用于科学计算的,尾数一定会不精确的,所以不能用==比较,Java可以用Math.abs(fVar-0.02) < 0.0000001表示等于,或者直接用Double.compare(d1, d2)比较,C也一样。
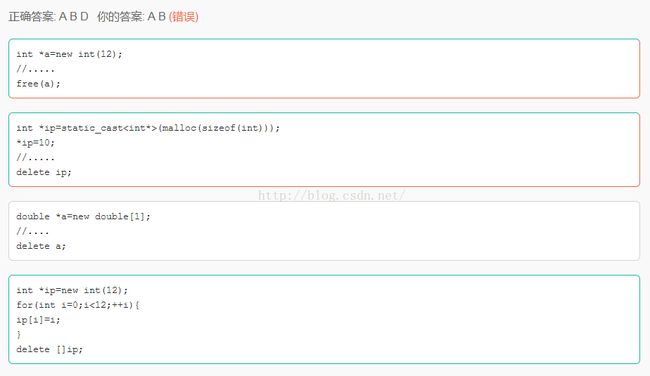
D是因为申请的是一个元素,后面跟的12是初始化值,而不是数组,所以错误。
new和delete与free和malloc的差别是前面2个会分别调用构造函数和析构函数