后缀树系列一:概念以及实现原理（ the Ukkonen algorithm）

首先说明一下后缀树系列一共会有三篇文章，本文先介绍基本概念以及如何线性时间内构件后缀树，第二篇文章会详细介绍怎么实现后缀树（包含实现代码），第三篇会着重谈一谈后缀树的应用。

 

本文分为三个部分，

• 首先介绍一下后缀树的“前身”-- trie树以及后缀树的概念；
• 然后介绍一下怎么通过trie树在平方时间内构件后缀树；
• 最后介绍一下怎么改进从而可以在线性时间内构件后缀树；

一，从trie树到后缀树

       在接触后缀树之前先简单聊聊trie树，也就是字典树。trie树有三个性质：

• 根节点不包含字符，除根节点外每一个节点都只包含一个字符。
• 从根节点到某一节点，路径上经过的字符连接起来，为该节点对应的字符串。
• 每个节点的所有子节点包含的字符都不相同。

    

       将一系列字符串插入到trie树的过程可以这样来实现：首先，树根不存任何字符；对于每个字符串，从左到右，沿着树从根节点开始往下走直到找不到“路”可以走的时候，“自己开辟一条路”继续往下走。比如往trie树里面存放ana,ann ,ann, anna,以及anne ,以及anne是个字符串的时候（注意一下，$是用来标志字符串末尾），我们会的到这样一棵树：见下左图

上左图这样存储的时候有点浪费。为了更高效我们把没有分支的路径压缩，于是得到上右图。很简单吧

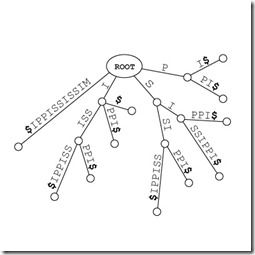
      介绍完trie树之后呢，我们再来看一看后缀，直接列出一个字符串MISSISSIPPI的所有后缀

1. MISSISSIPPI
2.   ISSISSIPPI
3.    SSISSIPPI
4.      SISSIPPI
5.        ISSIPPI
6.         SSIPPI
7.           SIPPI
8.             IPPI
9.              PPI
10.              PI
11.               I

而将这些后缀全部插入前面提到的trie树中并压缩，就得到后缀树啦

 

二，两种方法在平方时间内构件后缀树

　　所谓的平方时间是指O(|T|*|T|)，|T|是指字符串的长度。

　　第一种方法非常显然，就是直接按照后缀树的定义来就可以了，将各个后缀依次插入trie树中，再压缩，总的时间复杂度显然是平方级别的。

　　这里给出的是另外一种方法。对照上面MISSISSIPPI的所有后缀，我们注意到第一种方法就是从左到右扫描完一个后缀再从上到下扫描所有的后缀。那么另外一种思路就是，先安位对齐，然后从上到下扫描完每个位，再从左到右扫描下一位。举个例子吧，第一种方法相当于先扫描完后缀１：MISSISSIPPI ，再往下扫描后缀２：ISSISSIPPI 以此类推；而第二种方法相当于从上到下先插入第一个字符M，然后再从上到下插入第二个字符I(有两个)，然后再从上到下插入字符S(有三个)以此类推，参见下图。

　　但是具体怎么操作呢？因为显然每次操作不能是简简单单的插入字符而已！

　　我们再后头来看看上述过程，形式化一点，我们将原先的字符串表示为

　　T = t1t2 … tn$，其中ti表示第i个字符

　　Pi = t1t2 … ti ， i:th prefix of T

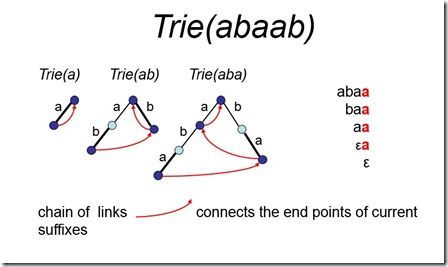
　　那么，我们每次插入字符ti，相当于完成一个从Trie(Pi-1)到Trie(Pi)的过程，当所有字符插入完毕的时候我们整个后缀树也就构建出来了。参见下图：插入第二个字符b相当于完成了从Trie(a)到Trie(ab)的过程。。。。

　　那我们怎么做呢？

　　上图中也提示了，其实我们需要额外保留一个尾部链表，连接着当前的“尾部”节点－－也就是对应着Pi的一个后缀的那些个点。我们注意到尾部链表实际上是从表示T[0 .. i]后缀的点指向表示T[1 .. i]后缀的点再指向表示T[2 .. i]后缀的点，以此类推。

　　也可以看得出来，每次插入一个字符都需要遍历一下链表，第一次遍历的时候链表长度为1(就是根节点),第二次遍历的时候链表长度为2(点a,和根节点，参见Trie(a) )，以此类推，可知遍历的总复杂度是O(|T|*|T|)，建立链表也需要O(|T|*|T|)，后续压缩Trie也需要O(|T|*|T|)，故而整个算法复杂度就是O(|T|*|T|)。

　　现在说明一下为什么算法是正确的？Trie(Pi-1)存储的是Pi-1的所有后缀，Trie(Pi)存储的是Pi的所有后缀。Pi的后缀可以由Pi-1所有后缀后面插入字符ti，以及后缀ti所构成。那么我们沿着Trie(Pi-1)尾部链表插入字符ti的过程也就是插入Pi的所有后缀的过程，所有算法是正确的。

　　但是，有没有小失望，毕竟干了这么久发现跟第一种方法相比没有收益（哭！）。

　　其实不用失望，我们做这么多的目的在于通过改进，整个算法可以实现线性的，下面就一步步介绍这种改进算法。

 

三，改进第二种算法以实现线性时间建立后缀树

　　1 直接在后缀树上操作　　

　　首先一点我们必须直接在后缀树上操作了，不能先建立Trie树再压缩，因为遍历Trie树的复杂度就已经是平方级别了。

　　我们定义几种节点：

• 　　叶节点：   出现在后缀树叶子上的节点；
• 　　显式节点：所有出现在后缀树中的节点。显然叶节点也是显示节点；
• 　　内部节点：显示节点中不是叶子节点的所有节点；
• 　　隐式节点：出现在Trie树中但是没有出现在后缀树中的点；（因为路径压缩）

 

　　接下来我们来看看前面提到的尾部链表，尾部链表显然包含了当前后缀树中的叶节点以及部分的显式/隐式节点。沿着尾部链表更新:

• 遇到叶子节点时只需往叶子所在的边上面的字符串后面插入字符就好了，不用改变树的结构；
• 遇到显式节点的时候，先看看插入的字符是否出现在显式节点后紧跟的字符集合中（比如上图中红色的显式节点后紧跟的字符集和就是｛s,p｝）,如果插入的字符出现在集合中，那么什么也不要做（是指不用改变树的结构），因为已经存在了；如果没有出现，在显式节点后面增加一个叶子，边上标注为这个字符。
• 遇到隐式节点时，一样，先看看隐式节点后面的字符是不是当前将要插入的字符，如果有则不用管了，没有则需要将当前隐式节点变为显式节点，再增加新叶子。

　　我们用个例子来说明一下怎么操作，为了便于说明隐式节点，我采用Trie树表示：

 

　　从第三个图到第四个图，沿着尾部链表插入字符a，那么链表第一个节点为叶节点，故而直接在边上插入这个字符就好了；链表第二个节点还是叶子，在边上插入字符就好了；第三个节点是隐式节点，看看紧跟着隐式节点后面的字符，不是a，故而将这个隐式节点变为显式节点，再增加一个叶子；第四个是显式节点（根节点），其紧跟的字符集和为{a,b}，a出现在这个集合中，故而不用改变结构了。当然了，链表还是要维护的啊，Ｏ（∩＿∩）Ｏ哈哈～

　　好了，到此，我们实现了直接在后缀树上操作而完全撇开Trie树了，小有进步啦，～＼（≧▽≦）／～啦啦啦

　　现在开始优化啦！

　　2.  自动更新叶节点

　　首先一点，在后缀树上直接操作的时候，边上的字符串就没必要直接存储啦，我们可以存这个字符串对于在原先总的字符串T中的坐标。如上方右边那个图就是将左边第四个图，压缩之后得到的后缀树。[2,4]就表示baa。

　　这样一来啊，存储后缀树的空间就大大减小了。

　　接着，我们来看一下啊，后缀树S(Pi-1)中的叶子节点在S(Pi)中也是叶子节点，也就是说”一朝为叶，终身为叶“。而且我们还可以注意到尾部链表的前半部分全是叶子。也就是说如果S(Pi)有k个叶子，那么表示T[0 .. i]，……，T[k-1 .. i]后缀的点全是叶子。

　　我们首先来看一下什么时候后缀会不在叶子上：T[j .. i-1]不在S(Pi-1)叶子上，表明代表该后缀的点之后还有点存在，也就是说T[0 .. i-1]中存在子串S=T[j .. i-1] + c’ ，其中c'不为空。注意一下这是充分必要条件，因为叶子节点后面是不可能还存在点的。

　　现在我们来证明一下：（ti加入到 S(Pi-1) 的过程）

• • 首先，T[0 .. i-1]肯定在叶子上。为什么呢，因为在S(Pi-1)中T[0 .. i-1]是最长的，如果它不在叶子上，那么必然存在比T[0 - i-1]还长的串，矛盾，故而T[0 .. i-1]一定在叶子上。
  • 其次，对于任何 j < i-1， 如果 T[j .. i-1] 不在树叶上，那么 T[j+1 .. i-1] 更不可能在树叶上；为什么呢，因为T[j .. i-1]不在叶子上表明T[0 .. i-1]中存在子串S=T[j .. i-1] + c’ ，其中c'不为空。那么T[0 .. i-1]中y也必然存在子串S‘=T[j+1 .. i-1] + c’，因为S’是S的后缀。故而 T[j+1 .. i-1]也不在叶子上
  • 于是我们知道k个叶子一定是T[0 .. i]，……，T[k-1 .. i]

　　我们来利用一下上述性质。叶节点每次更新都是把ti插入到叶子所在边的后缀字符串中，所以表示字符串的区间就变成了[ , ｉ]。那么我们还有必要每次都沿着尾部链表去更新么？

　　我们可以这样，将叶子那个边上的表示字符串的区间用[ , #]来表示，#表示当前插入字符在T中的下标。那么这样一来，叶子节点就自动更新啦。

　　再利用第二个性质，我们完全就可以不管尾部链表的前k个节点啦。

　　这是又一大进步！

　　咱们接着来！

　　3. 当新后缀出现在原先后缀树中

　　我们来看，根据沿尾部链表更新的算法，无论是显式节点还是隐式节点，当带插入字符ti出现在节点的紧跟字符集合的时候，我们就不用管了。也就是说如果T[j .. i]出现在S(Pi-1)，也就是S(T[0 .. i-1])，中的时候，我们就不用改变树的结构了（当然需要还调整一些参数）。

　　我们再来看，对于任何 j < i-1，如果T[j .. i]出现在S(T[0 .. i-1])中，那么T[j+1 .. i]也必然出现在S(T[0 .. i-1])中。下面给出证明：

• 首先我们知道T[0..i-1] 的所有后缀都在后缀树中。
• 其次，T[0..i-1] 的任意子串都可以表示为它的某一个后缀的前缀。
• 所以 T[0..i-1] 的所有子串都在后缀树中。
• T[j+1 .. i] 是 T[j..i] 的子串， T[j..i] 又是 T[0..i-1] 的子串（因为T[j .. i]出现在S(T[0 .. i-1])中），所以 T[j+1 .. i] 也是 T[0..i-1] 的子串。
• 所以后缀树中存在 T[j+1 .. i]

　　这也就是说如果尾部链表中某一个节点所代表的后缀加上ti，也就是T[j .. i]，出现在S(T[0 .. i-1])中,那么链表后面的所有节点代表的后缀加上ti也都出现在S(T[0 .. i-1])中。

　　故而所有这些点，无论是显式还是隐式节点都可以不用管了。

　　这又是一个大优化！

　　综合上面两个优化，我们知道事实上我们只需要处理原先尾部链表的中间一段节点就可以了，对于这些节点而言，每处理一次必定增加一个新叶子（为什么呢，因为这些节点既不是叶子节点，又不满足显或是隐式节点不用增加叶子的条件）。而”一朝为叶，终身为叶“，我们最终的后缀树S(T[0 .. n])只有n个叶子(其中tn=)。（为什么呢，因为不可能存在子串S=T[j..n]+c ′ ，因为这要求子串中 )。（为什么呢，因为不可能存在子串S=T[j..n]+c′，因为这要求子串中之后还有字符，这是办不到的），这也就是说整个建树过程中我们一共只需要在尾部链表上处理n次就可以了，这是一个好兆头！

　　种种迹象表明我们快到O(|T|)时间了，哈哈，原理就先说这么多了。能不能实现最终的线性时间，就看下一节－－线性时间内构建后缀树！

 

四　引用

１. http://www.cnblogs.com/snowberg/archive/2011/10/21/2468588.html

2.  http://blog.csdn.net/v_july_v/article/details/6897097

3.  On–line construction of suffix trees

转载地址：

http://www.cnblogs.com/xubenben/p/3484988.html