- LocalDateTime 转 String
igotyback
java开发语言
importjava.time.LocalDateTime;importjava.time.format.DateTimeFormatter;publicclassMain{publicstaticvoidmain(String[]args){//获取当前时间LocalDateTimenow=LocalDateTime.now();//定义日期格式化器DateTimeFormatterformat
- 如何在 Fork 的 GitHub 项目中保留自己的修改并同步上游更新?github_fork_update
iBaoxing
github
如何在Fork的GitHub项目中保留自己的修改并同步上游更新?在GitHub上Fork了一个项目后,你可能会对项目进行一些修改,同时原作者也在不断更新。如果想要在保留自己修改的基础上,同步原作者的最新更新,很多人会不知所措。本文将详细讲解如何在不丢失自己改动的情况下,将上游仓库的更新合并到自己的仓库中。问题描述假设你在GitHub上Fork了一个项目,并基于该项目做了一些修改,随后你发现原作者对
- SpringBlade dict-biz/list 接口 SQL 注入漏洞
文章永久免费只为良心
oracle数据库
SpringBladedict-biz/list接口SQL注入漏洞POC:构造请求包查看返回包你的网址/api/blade-system/dict-biz/list?updatexml(1,concat(0x7e,md5(1),0x7e),1)=1漏洞概述在SpringBlade框架中,如果dict-biz/list接口的后台处理逻辑没有正确地对用户输入进行过滤或参数化查询(PreparedSta
- 2024.9.14 Python,差分法解决区间加法,消除游戏,压缩字符串
RaidenQ
python游戏开发语言算法力扣
1.区间加法假设你有一个长度为n的数组,初始情况下所有的数字均为0,你将会被给出k个更新的操作。其中,每个操作会被表示为一个三元组:[startIndex,endIndex,inc],你需要将子数组A[startIndex…endIndex](包括startIndex和endIndex)增加inc。请你返回k次操作后的数组。示例:输入:length=5,updates=[[1,3,2],[2,4,
- 使用datepicker和uploadify的冲突解决(IE双击才能打开附件上传对话框)
zhanglb12
在开发的过程当中,IE的兼容无疑是我们的一块绊脚石,在我们使用的如期的datepicker插件和使用上传附件的uploadify插件的时候,两者就产生冲突,只要点击过时间的插件,uploadify上传框要双才能打开ie浏览器提示错误Missinginstancedataforthisdatepicker解决方案//if(.browser.msie&&'9.0'===.browser.version
- 360前端星计划-动画可以这么玩
马小蜗
动画的基本原理定时器改变对象的属性根据新的属性重新渲染动画functionupdate(context){//更新属性}constticker=newTicker();ticker.tick(update,context);动画的种类1、JavaScript动画操作DOMCanvas2、CSS动画transitionanimation3、SVG动画SMILJS动画的优缺点优点:灵活度、可控性、性能
- k8s证书过期问题处理
olina_qin
kubernetes容器云原生
k8s证书过期问题处理opensslx509-in/etc/kubernetes/pki/apiserver.crt-noout-dateskubeadmcertsrenewallsystemctlrestartkubeleopensslx509-in/etc/kubernetes/pki/apiserver.crt-noout-text|grep"NotAfter"cp/etc/kubernet
- 华南农业大学C语言oj第八章
黑兔子撒
C语言C语言华南农业大学编程程序
18058一年的第几天时间限制:1000MS内存限制:65535K提交次数:0通过次数:0题型:填空题语言:G++;GCC;VCDescription定义一个结构体类型表示日期类型(包括年、月、日)。程序中定义一个日期类型的变量,输入该日期的年、月、日,计算并输出该日期是一年的第几天。#include struct DATE { _______________________ }; int da
- pythonpandas函数详解_Python pandas常用函数详解
Senvn
本文研究的主要是pandas常用函数,具体介绍如下。1import语句importpandasaspdimportnumpyasnpimportmatplotlib.pyplotaspltimportdatetimeimportre2文件读取df=pd.read_csv(path='file.csv')参数:header=None用默认列名,0,1,2,3...names=['A','B','C'
- linux简单安装gcc和gdb
chn-zgq
Linuxlinuxubuntu
linux安装gcc以及环境配置和gdb安装gcc-10.0添加源:sudoadd-apt-repositoryppa:ubuntu-toolchain-r/ppa更新源:sudoaptupdate下载gcc:sudoaptinstallgcc-10g++-10默认GCC版本设置为gcc-10.0:sudoupdate-alternatives--install/usr/bin/gccgcc/us
- Linux使用mjpg-streamer进行图像传输
—你的鼬先生
Linux驱动linux树莓派图像传输
图像传输是一项在Linux操作系统中比较常见的一个操作,在视频图传时,一般是采用MJPG-streamer来进行图像传输,本文就以树莓派为例子,来示范一个图像传输。1.树莓派的摄像头激活首先更新树莓派sudoapt-getupdatesudoapt-getupgrade随后打开树莓派的配置界面,选择InterfaceOptionsudoraspi-config在InterfaceOption选择C
- MySQL锁
沉着冷静2024
MySQLmysql数据库
MySQL锁文章目录MySQL锁MySQL中锁的分类创建索引时会锁表吗线上修改表结构会加什么锁Innodb存储引擎的行级锁有哪些Update语句中,不带where条件,加什么锁?MySQL实现乐观锁MySQL死锁MySQL死锁是怎么发生的?检查死锁如何避免死锁MySQL中锁的分类全局锁:主要用于全库逻辑备份表级锁:表锁、元数据锁、意向锁表锁:通过locktables语句对表进行加锁,它不仅限制其他
- python如何更方便的处理日期和时间
openwin_top
python编程示例系列python编程示例系列二pythonjava前端
Arrow是一个第三方Python库,提供了更加易用和方便的日期和时间处理接口。它的设计目标是提供一种简单、一致且易于使用的API,以替代Python内置的datetime模块。Arrow支持各种日期和时间的操作,包括时区转换、日期和时间格式化、日期和时间差计算等功能。它还支持与其他日期和时间库的互操作,例如datetime、dateutil和pandas等库。以下是一个使用Arrow库的简单示例
- php状态监控源码,PHP服务器状态监控实现程序
江子星
php状态监控源码
*/header('Content-type:text/html;charset=utf-8');include'./smtp/class.smtp.php';include'./smtp/class.phpmailer.php';functionsendmail($subject='',$body=''){date_default_timezone_set('Asia/Shanghai');//
- 关于UI刷新重绘
草帽小子J
最近做了一个关于用户雷达图的需求,有用到关于ui绘制相关的东西,于是去了解了下关于invalidate()、postInvalidate()、requestLayout()的知识。invalidate该方法会请求重绘view树,即draw(),刷新UI,并且不会调用onMeasure(),谁调用重绘谁,ViewGroup则重绘整个ViewGroup.一般会触发invalidate的主要为如下几种方
- 数据库常见笔试面试题及其解析
yxsr_zxx
数据库数据库SqlServerOracle笔试面试
数据库基础(面试常见题)一、数据库基础1.数据抽象:物理抽象、概念抽象、视图级抽象,内模式、模式、外模式2.SQL语言包括数据定义、数据操纵(DataManipulation),数据控制(DataControl)数据定义:CreateTable,AlterTable,DropTable,Craete/DropIndex等数据操纵:Select,insert,update,delete,数据控制:g
- git 恢复误删的远程分支
Hanfank
需求实际工作上,肯定会有不小心的时候,比如我吧,删除了本地dev分支,intellijidea提示是否将trackedbranch也删掉,结果一不小心将远程分支也删除了,接下来就是我的救赎之旅。查看reflog,找到最后一次commitidgitreflog--date=isoreflog是referencelog的意思,也就是引用log,记录HEAD在各个分支上的移动轨迹。选项--date=is
- Nuxt Kit 自动导入功能:高效管理你的模块和组合式函数
qcidyu
好用的工具集合代码效率前端技巧Vue开发组合式函数模块管理自动导入NuxtKit
title:NuxtKit自动导入功能:高效管理你的模块和组合式函数date:2024/9/14updated:2024/9/14author:cmdragonexcerpt:通过使用NuxtKit的自动导入功能,您可以更高效地管理和使用公共函数、组合式函数和VueAPI。无论是单个导入、目录导入还是从第三方模块导入,您都可以通过简单的API调用轻松实现。categories:前端开发tags:N
- STM32 的 RTC(实时时钟)详解
千千道
STM32stm32物联网单片机
目录一、引言二、RTC概述三、RTC的工作原理1.时钟源2.计数器3.闹钟功能4.备份寄存器四、RTC寄存器1.RTC_TR(TimeRegister,时间寄存器)2.RTC_DR(DateRegister,日期寄存器)3.RTC_SSR(SubsecondRegister,亚秒寄存器)4.RTC_PRER(PrescalerRegister,预分频器寄存器)5.RTC_CR(ControlReg
- 互联网 Java 工程师面试题(Java 面试题四)
苹果酱0567
面试题汇总与解析java中间件开发语言springboot后端
下面列出这份Java面试问题列表包含的主题多线程,并发及线程基础数据类型转换的基本原则垃圾回收(GC)Java集合框架数组字符串GOF设计模式SOLID抽象类与接口Java基础,如equals和hashcode泛型与枚举JavaIO与NIO常用网络协议Java中的数据结构和算法正则表达式JVM底层Java最佳实JDBCDate,Time与CalendarJava处理XMLJUnit编程现在是时候给
- Java:日期类2
昭关969
java开发语言
SimpleDateFormat日期格式化类构造SimpleDateFormat(Stringpattern);pattern是我们自己制定的日期格式,字母不能改变,但连接符可以改变yyyy--MM--dd--HH时间单位字母表示Y年M月d日H时m分s秒方法Stringformat(Datedate)将Date对象按照对应格式转成StringDateparse(Stringsource)将符合我们
- 利用apache-pdfbox库修改pdf文件模板,进行信息替换
区块链攻城狮
pdf合同模板pdf生成合同生成
publicStringcreateSignFile(Longid)throwsIOException{//1.验证企业信息CompanyDOcompany=validateCompanyExists(id);//2.验证签约状态if(company.getSignStatus()!=0){throwexception(COMPANY_SIGN_STATUS_NOT_ZERO);}//3.获取合同
- 在CentOS 7上安装桌面环境可以通过以下步骤完成
开心呆哥
linux服务器运维
确保您的系统已连接到互联网,并使用root权限登录。运行以下命令以更新系统软件包:yumupdate安装桌面环境的软件包组。CentOS7提供了几个桌面环境选择,包括GNOME、KDE、Xfce等。选择其中一个环境进行安装。例如,要安装GNOME桌面环境,运行以下命令:yumgroupinstall"GNOMEDesktop"如果要安装KDE桌面环境,将命令中的"GNOMEDesktop"替换为"
- Unity中的FixedUpdate、Update、LateUpdate的区别及游戏帧更新
永恒星
UnityFixedUpdateUpdateLateUpdate
【基本了解】三者执行顺序:FixedUpdate——>Update——>LateUpdate三者作用:FixedUpdate固定帧更新,一般用作物理更新;Update一般用作游戏逻辑更新;LateUpdate一般用作相机更新【深入了解】帧率的概念帧率是什么呢?一秒内画面更新的次数。游戏常用的有30fps,60fps。我们知道,帧率低游戏会卡顿,具体解释下就是,每秒内看到的画面更新次数变少,少于一个
- 钉钉自定义机器人
AlphaHinex
原文地址:https://alphahinex.github.io/2022/03/06/dingtalk-custom-robot/description:"像发手机短信一样方便"date:2022.03.0610:34categories:-DevOpstags:[Dingtalk,Robot]keywords:dingtalk,robot,钉钉,机器人,聊天机器人聊天机器人从hubot起接触
- 自己实现一个简易RPC调用框架
殷俊杰
最近在看dubbo,去创始人之一梁飞大神的博客搂了几眼,找到这个demo自己实现了一下,关于dubbo就不再介绍了,快速开始、框架设计、设计原则官网都有,有兴趣可以自己看Dubbo官网1.服务接口packagecom.yjj.my.api;/***@Description:*@Author:yinjunjie*@CreateDate:2018/8/713:16*@Version:1.0*/publ
- 【Java实战】使用自定义注解实现参数校验详解
.猫的树
【Java实战】系列java自定义注解参数校验
文章目录前言一、Java注解简介二、启用注解校验1.启用注解2.注解@Valid和@Validated2.1@Valid级联校验2.2@Validated高级使用三、自定义注解1.统一异常处理2.编写注解2.1自定义校验2.2多参数校验2.3列表校验总结前言由于实际开发中遇到大量相同的条件参数验证,不想写重复代码及让代码看起来更加优雅简洁,所以决定使用自定义注解进行参数校验一、Java注解简介Ja
- ssh安装,配置以及免密连接
叶域
环境配置与项目部署sshlinux
ssh安装,配置以及免密连接目录:一、ssh检查与安装二、ssh基本用法三、配置文件(~/.ssh/config)四、ssh免密连接五、通过ssh在服务器执行命令一、ssh检查与安装sudosystemctlstatusssh#检查SSH服务器状态一般linux系统都自带ssh,如果没有可以根据如下命令安装sudoaptupdate#更新数据sudoaptupgrade#更新软件sudoaptin
- unocss 一直热更新打印[vite] hot updated: /__uno.css
柳雾青烟紫燕穿
csscss3vue
控制台持续打印了几千条这条信息,页面逐渐卡死client.ts:450[vite]hotupdated:/__uno.css找出的原因是:依赖出问题了,重新安装unocss,执行命令npmiunocss后修复。但奇怪的是,删除node_modules重新全部安装依赖却不能修复,tmd。还有一种解决方法是切换分支,切去其它分支,再切回来,也不会再打印了。一开始还怀疑了是哪里的unocss类名一直在监
- SQL server CROSS JOIN 的用法
潇锐killer
数据库sql
SELECT@DateThresholdasdt,t3.ck_id,t3.ck_name,t3.title_id,t3.title,casewhent4.numisnullthen0elset4.numendnum,casewhent4.moneyisnullthen0elset4.moneyendmoney,t3.startDay,t3.endDayfrom(SELECTt1.ck_id,t1.
- 安装数据库首次应用
Array_06
javaoraclesql
可是为什么再一次失败之后就变成直接跳过那个要求
enter full pathname of java.exe的界面
这个java.exe是你的Oracle 11g安装目录中例如:【F:\app\chen\product\11.2.0\dbhome_1\jdk\jre\bin】下的java.exe 。不是你的电脑安装的java jdk下的java.exe!
注意第一次,使用SQL D
- Weblogic Server Console密码修改和遗忘解决方法
bijian1013
Welogic
在工作中一同事将Weblogic的console的密码忘记了,通过网上查询资料解决,实践整理了一下。
一.修改Console密码
打开weblogic控制台,安全领域 --> myrealm -->&n
- IllegalStateException: Cannot forward a response that is already committed
Cwind
javaServlets
对于初学者来说,一个常见的误解是:当调用 forward() 或者 sendRedirect() 时控制流将会自动跳出原函数。标题所示错误通常是基于此误解而引起的。 示例代码:
protected void doPost() {
if (someCondition) {
sendRedirect();
}
forward(); // Thi
- 基于流的装饰设计模式
木zi_鸣
设计模式
当想要对已有类的对象进行功能增强时,可以定义一个类,将已有对象传入,基于已有的功能,并提供加强功能。
自定义的类成为装饰类
模仿BufferedReader,对Reader进行包装,体现装饰设计模式
装饰类通常会通过构造方法接受被装饰的对象,并基于被装饰的对象功能,提供更强的功能。
装饰模式比继承灵活,避免继承臃肿,降低了类与类之间的关系
装饰类因为增强已有对象,具备的功能该
- Linux中的uniq命令
被触发
linux
Linux命令uniq的作用是过滤重复部分显示文件内容,这个命令读取输入文件,并比较相邻的行。在正常情 况下,第二个及以后更多个重复行将被删去,行比较是根据所用字符集的排序序列进行的。该命令加工后的结果写到输出文件中。输入文件和输出文件必须不同。如 果输入文件用“- ”表示,则从标准输入读取。
AD:
uniq [选项] 文件
说明:这个命令读取输入文件,并比较相邻的行。在正常情况下,第二个
- 正则表达式Pattern
肆无忌惮_
Pattern
正则表达式是符合一定规则的表达式,用来专门操作字符串,对字符创进行匹配,切割,替换,获取。
例如,我们需要对QQ号码格式进行检验
规则是长度6~12位 不能0开头 只能是数字,我们可以一位一位进行比较,利用parseLong进行判断,或者是用正则表达式来匹配[1-9][0-9]{4,14} 或者 [1-9]\d{4,14}
&nbs
- Oracle高级查询之OVER (PARTITION BY ..)
知了ing
oraclesql
一、rank()/dense_rank() over(partition by ...order by ...)
现在客户有这样一个需求,查询每个部门工资最高的雇员的信息,相信有一定oracle应用知识的同学都能写出下面的SQL语句:
select e.ename, e.job, e.sal, e.deptno
from scott.emp e,
(se
- Python调试
矮蛋蛋
pythonpdb
原文地址:
http://blog.csdn.net/xuyuefei1988/article/details/19399137
1、下面网上收罗的资料初学者应该够用了,但对比IBM的Python 代码调试技巧:
IBM:包括 pdb 模块、利用 PyDev 和 Eclipse 集成进行调试、PyCharm 以及 Debug 日志进行调试:
http://www.ibm.com/d
- webservice传递自定义对象时函数为空,以及boolean不对应的问题
alleni123
webservice
今天在客户端调用方法
NodeStatus status=iservice.getNodeStatus().
结果NodeStatus的属性都是null。
进行debug之后,发现服务器端返回的确实是有值的对象。
后来发现原来是因为在客户端,NodeStatus的setter全部被我删除了。
本来是因为逻辑上不需要在客户端使用setter, 结果改了之后竟然不能获取带属性值的
- java如何干掉指针,又如何巧妙的通过引用来操作指针————>说的就是java指针
百合不是茶
C语言的强大在于可以直接操作指针的地址,通过改变指针的地址指向来达到更改地址的目的,又是由于c语言的指针过于强大,初学者很难掌握, java的出现解决了c,c++中指针的问题 java将指针封装在底层,开发人员是不能够去操作指针的地址,但是可以通过引用来间接的操作:
定义一个指针p来指向a的地址(&是地址符号):
- Eclipse打不开,提示“An error has occurred.See the log file ***/.log”
bijian1013
eclipse
打开eclipse工作目录的\.metadata\.log文件,发现如下错误:
!ENTRY org.eclipse.osgi 4 0 2012-09-10 09:28:57.139
!MESSAGE Application error
!STACK 1
java.lang.NoClassDefFoundError: org/eclipse/core/resources/IContai
- spring aop实例annotation方法实现
bijian1013
javaspringAOPannotation
在spring aop实例中我们通过配置xml文件来实现AOP,这里学习使用annotation来实现,使用annotation其实就是指明具体的aspect,pointcut和advice。1.申明一个切面(用一个类来实现)在这个切面里,包括了advice和pointcut
AdviceMethods.jav
- [Velocity一]Velocity语法基础入门
bit1129
velocity
用户和开发人员参考文档
http://velocity.apache.org/engine/releases/velocity-1.7/developer-guide.html
注释
1.行级注释##
2.多行注释#* *#
变量定义
使用$开头的字符串是变量定义,例如$var1, $var2,
赋值
使用#set为变量赋值,例
- 【Kafka十一】关于Kafka的副本管理
bit1129
kafka
1. 关于request.required.acks
request.required.acks控制者Producer写请求的什么时候可以确认写成功,默认是0,
0表示即不进行确认即返回。
1表示Leader写成功即返回,此时还没有进行写数据同步到其它Follower Partition中
-1表示根据指定的最少Partition确认后才返回,这个在
Th
- lua统计nginx内部变量数据
ronin47
lua nginx 统计
server {
listen 80;
server_name photo.domain.com;
location /{set $str $uri;
content_by_lua '
local url = ngx.var.uri
local res = ngx.location.capture(
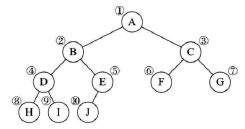
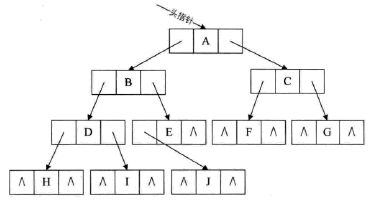
- java-11.二叉树中节点的最大距离
bylijinnan
java
import java.util.ArrayList;
import java.util.List;
public class MaxLenInBinTree {
/*
a. 1
/ \
2 3
/ \ / \
4 5 6 7
max=4 pass "root"
- Netty源码学习-ReadTimeoutHandler
bylijinnan
javanetty
ReadTimeoutHandler的实现思路:
开启一个定时任务,如果在指定时间内没有接收到消息,则抛出ReadTimeoutException
这个异常的捕获,在开发中,交给跟在ReadTimeoutHandler后面的ChannelHandler,例如
private final ChannelHandler timeoutHandler =
new ReadTim
- jquery验证上传文件样式及大小(好用)
cngolon
文件上传jquery验证
<!DOCTYPE html>
<html>
<head>
<meta http-equiv="Content-Type" content="text/html; charset=utf-8" />
<script src="jquery1.8/jquery-1.8.0.
- 浏览器兼容【转】
cuishikuan
css浏览器IE
浏览器兼容问题一:不同浏览器的标签默认的外补丁和内补丁不同
问题症状:随便写几个标签,不加样式控制的情况下,各自的margin 和padding差异较大。
碰到频率:100%
解决方案:CSS里 *{margin:0;padding:0;}
备注:这个是最常见的也是最易解决的一个浏览器兼容性问题,几乎所有的CSS文件开头都会用通配符*来设
- Shell特殊变量:Shell $0, $#, $*, $@, $?, $$和命令行参数
daizj
shell$#$?特殊变量
前面已经讲到,变量名只能包含数字、字母和下划线,因为某些包含其他字符的变量有特殊含义,这样的变量被称为特殊变量。例如,$ 表示当前Shell进程的ID,即pid,看下面的代码:
$echo $$
运行结果
29949
特殊变量列表 变量 含义 $0 当前脚本的文件名 $n 传递给脚本或函数的参数。n 是一个数字,表示第几个参数。例如,第一个
- 程序设计KISS 原则-------KEEP IT SIMPLE, STUPID!
dcj3sjt126com
unix
翻到一本书,讲到编程一般原则是kiss:Keep It Simple, Stupid.对这个原则深有体会,其实不仅编程如此,而且系统架构也是如此。
KEEP IT SIMPLE, STUPID! 编写只做一件事情,并且要做好的程序;编写可以在一起工作的程序,编写处理文本流的程序,因为这是通用的接口。这就是UNIX哲学.所有的哲学真 正的浓缩为一个铁一样的定律,高明的工程师的神圣的“KISS 原
- android Activity间List传值
dcj3sjt126com
Activity
第一个Activity:
import java.util.ArrayList;import java.util.HashMap;import java.util.List;import java.util.Map;import android.app.Activity;import android.content.Intent;import android.os.Bundle;import a
- tomcat 设置java虚拟机内存
eksliang
tomcat 内存设置
转载请出自出处:http://eksliang.iteye.com/blog/2117772
http://eksliang.iteye.com/
常见的内存溢出有以下两种:
java.lang.OutOfMemoryError: PermGen space
java.lang.OutOfMemoryError: Java heap space
------------
- Android 数据库事务处理
gqdy365
android
使用SQLiteDatabase的beginTransaction()方法可以开启一个事务,程序执行到endTransaction() 方法时会检查事务的标志是否为成功,如果程序执行到endTransaction()之前调用了setTransactionSuccessful() 方法设置事务的标志为成功则提交事务,如果没有调用setTransactionSuccessful() 方法则回滚事务。事
- Java 打开浏览器
hw1287789687
打开网址open浏览器open browser打开url打开浏览器
使用java 语言如何打开浏览器呢?
我们先研究下在cmd窗口中,如何打开网址
使用IE 打开
D:\software\bin>cmd /c start iexplore http://hw1287789687.iteye.com/blog/2153709
使用火狐打开
D:\software\bin>cmd /c start firefox http://hw1287789
- ReplaceGoogleCDN:将 Google CDN 替换为国内的 Chrome 插件
justjavac
chromeGooglegoogle apichrome插件
Chrome Web Store 安装地址: https://chrome.google.com/webstore/detail/replace-google-cdn/kpampjmfiopfpkkepbllemkibefkiice
由于众所周知的原因,只需替换一个域名就可以继续使用Google提供的前端公共库了。 同样,通过script标记引用这些资源,让网站访问速度瞬间提速吧
- 进程VS.线程
m635674608
线程
资料来源:
http://www.liaoxuefeng.com/wiki/001374738125095c955c1e6d8bb493182103fac9270762a000/001397567993007df355a3394da48f0bf14960f0c78753f000 1、Apache最早就是采用多进程模式 2、IIS服务器默认采用多线程模式 3、多进程优缺点 优点:
多进程模式最大
- Linux下安装MemCached
字符串
memcached
前提准备:1. MemCached目前最新版本为:1.4.22,可以从官网下载到。2. MemCached依赖libevent,因此在安装MemCached之前需要先安装libevent。2.1 运行下面命令,查看系统是否已安装libevent。[root@SecurityCheck ~]# rpm -qa|grep libevent libevent-headers-1.4.13-4.el6.n
- java设计模式之--jdk动态代理(实现aop编程)
Supanccy2013
javaDAO设计模式AOP
与静态代理类对照的是动态代理类,动态代理类的字节码在程序运行时由Java反射机制动态生成,无需程序员手工编写它的源代码。动态代理类不仅简化了编程工作,而且提高了软件系统的可扩展性,因为Java 反射机制可以生成任意类型的动态代理类。java.lang.reflect 包中的Proxy类和InvocationHandler 接口提供了生成动态代理类的能力。
&
- Spring 4.2新特性-对java8默认方法(default method)定义Bean的支持
wiselyman
spring 4
2.1 默认方法(default method)
java8引入了一个default medthod;
用来扩展已有的接口,在对已有接口的使用不产生任何影响的情况下,添加扩展
使用default关键字
Spring 4.2支持加载在默认方法里声明的bean
2.2
将要被声明成bean的类
public class DemoService {
![]()
![]()
![]()
![]()
![]()
![]()