树状数组

树状数组

情景：在区间上进行以下两种操作(区间的初始值全部为0)
type1
A:把位置x的值+k
B:询问区间[l,r]之间所有数字之和
type2
A:把区间[l,r]上的值全都+x
B:询问x位置的值
type3
A:把区间[l,r]上的值全都+x
B:询问区间[l,r]上所有数字之和

所需了解的二进制按位运算的知识

1.按位与&

exp
0011 3
&1011 &11

---

0011 3

2.按位非~
₉₌1001=0110=6
3.n位的二进制数进行运算，一旦向第n+1位有进位，会直接舍去这个进位
4.计算机中，操作的变量通常有一个固定的位数，比如c++中的int32__t类型的变量
它用32位的二进制数来存储一个整数
在这个范围下
₁₌00000000000000000000000000000001=11111111111111111111111111111110

lowbit函数的介绍

lowbit(x)=x&((~x)+1)=x&-x
结果：只保留“从低位向高位数，第一个数字1”作为运算结果
exp：lowbit(00011100)=00000100=4
对本算法的作用：
先列举出1~32的lowbit
1 2 1 4 1 2 1 8 1 2 1 4 1 2 1 16 1 2 1 4 1 2 1 8 1 2 1 4 1 2 1 32

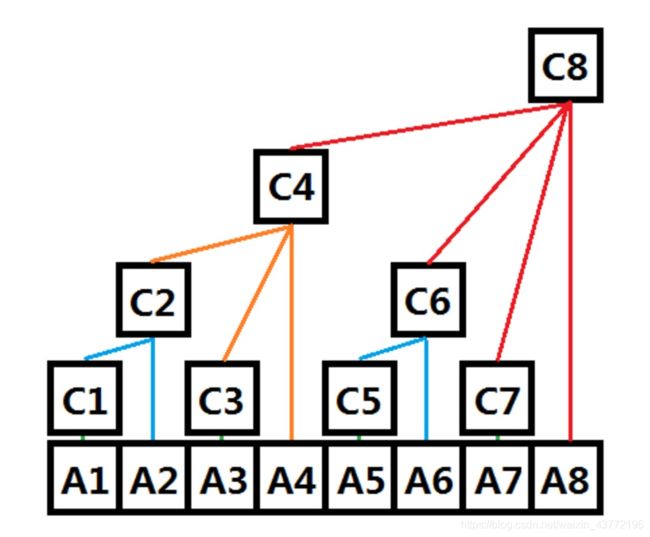
我们让第i个位置管理[i-lowbit(i)+1,i]这一段区间。
示意图如下

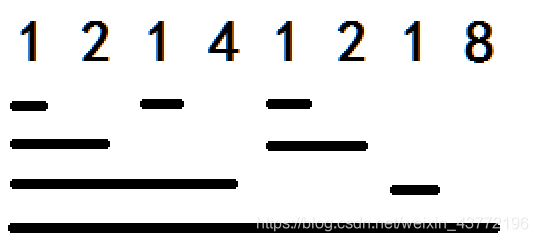
怎么看每个数字管理哪一段区间？
顺着数字向下划竖线，碰到的第一根横线所覆盖的范围就是它管理的区间

每次执行操作A（把位置x的值+k），只需要把“能管理到x的所有位置”都+k就行
那么怎么样能快速找到哪些位置能管理到x呢？
还是使用lowbit

我们先更新x位置的值，然后将x位置更新，即x=x+lowbit(x)，
新的位置x所管理的区间包含旧x的位置，这样依次类推直到x>10000即可

exp:
x=2;a[x]+=k
x=x+lowbit(x)=2+lowbit(2)=4;a[x]+=k;
x=x+lowbit(x)=4+lowbit(4)=8;a[x]+=k;
··············
x=······=16384>10000 break;
这样操作后，树状数组里每一位当前存的值可能不是该位置的实际值，为了方便区分
下文将实际值称作“原数组的值”，当前值称作“树状数组的值”

可以证明，对于任意x属于[1,10000]我们最多进行log(2,10000)次操作，就可以完成操作A
复杂度为O(logn)
复杂度A：O(1)–>O(logn)好处：操作B复杂度变为O(logn)

操作B:
求sum(l,r)
sum(l,r)=sum(1,r)-sum(1,l)
即如何求sum(1,x)
伪代码如下：
ans=0；
while(x>0)
{
ans+=a[x];
x=x-lowbit(x);
}
exp:
0.我们在进行“给原数组第x位置的数增加k”这个操作时，把“能管理到x的所有位置”都增加了k
那么，对于任意一个位置，树状数组的值(a[x])就是“它能管理到的所有位置上，原数组的值之和”sum(l,r)([l,r]∈x控制)
1.ans=0,此时我们停留在一开始的树状数组第x位置上(比如x=6)，
2.我们给ans加上ax，这里就得到了sum(5,6)，因为6管理的是[5,6]区间
3.x=x-lowbit(x),x=4，ans+=a[x]等价于ans+=a[4]，我们给答案加上树状数组第4位置的值(sum(1,4))
4.x=x-lowbit(x)=0<=0，end

type1复杂度=O((mA+mB)logn) 没有优化前的复杂度为O(mA+nmB)
(mA,mB为操作A,B执行的次数)

那么type2（A:把区间[l,r]上的值全都+x。B:询问x位置的值）怎么办呢？
用差分的方法，区间[l,r]所有值+k改成"位置l上加上k，位置r+1上减去k"
查询的时候直接查询sum(1,x）

type3（A:把区间[l,r]上的值全都+x。B:询问区间[l,r]上所有数字之和）怎么办呢
稍微复杂一点

用两个树状数组，分别叫做d和s

进行A操作时,d维护差分，s维护x*d[x]。

update(d,l,x);update(d,r+1,-x);

update(s,l,xl);update(s,r+1,-x(r+1));

进行B操作时

sum(L,R)=sum(1,R)-sum(1,L-1)

sum(1,L-1)=L*query(d,L-1)-query(s,L-1)

sum(1,R)=(R+1)*query(d,R)-query(s,R)

模板

简洁版

//简洁版
int tree[100010],n=100000;
void add(int x,int num)
{
	for(;x<=n;x+=x&-x)
		tree[x]+=num;
} 
int sum(int x)
{
	int answer =0;
	for(;x>0;x-=x&-x)
		answer+=tree[x];
	return answer;
} 

功能较全

/**
* 树状数组模板使用说明
* 以下将树状数组维护的区间称为原数组
* 操作             说明               时间复杂度     支持范围
* size()     返回树状数组的大小		 O(1)          ~
* resize(x)  重新指定树状数组的大小为x	 O(1)         x>=0
* add(i,v)   将原数组第i位增加v	         O(logn)    0<=i
#include
namespace OrangeOI
{
	template<typename Type>
	class BinaryIndexTree
	{
	private:
		size_t mSize;
		std::vector<Type> mArray;
		struct BinaryIndexTree_Node
		{
			BinaryIndexTree_Node(BinaryIndexTree& bit, size_t pos) :
				mBIT(bit), mPos(pos) {}
			const BinaryIndexTree_Node operator +=(Type value)
			{
				mBIT.add(mPos, value);
				return *this;
			}
			const BinaryIndexTree_Node operator -=(Type value)
			{
				mBIT.add(mPos, -value);
				return *this;
			}
			operator Type()
			{
				return mBIT.sum(mPos);
			}
		private:
			BinaryIndexTree& mBIT;
			size_t mPos;
		};
		int lowbit(int num)
		{
			return num&(~num + 1);
		}
	public:
		BinaryIndexTree() {}
		BinaryIndexTree(size_t size) :
			mSize(size)
		{
			mArray.resize(mSize);
		}
		virtual ~BinaryIndexTree() {}
		const size_t size()
		{
			return mSize;
		}
		void resize(size_t size)
		{
			mSize = size;
			mArray.resize(size);
		}
		void add(int index, Type value)
		{
			for (; index<mSize; index += lowbit(index + 1))
				mArray[index] += value;
		}
		Type sum(int index)
		{
			Type answer = Type();
			for (; index >= 0; index -= lowbit(index + 1))
				answer += mArray[index];
			return answer;
		}
		Type sum(int left, int right)
		{
			return sum(right) - sum(left - 1);
		}
		BinaryIndexTree_Node operator[](size_t pos)
		{
			return BinaryIndexTree_Node(*this, pos);
		}
	};
}

附录

简单差分

引入
给出n个数，再给出Q个询问，每个询问给出le，ri，x，要求你在le到ri上每一个值都加上x，而只给你O(n)的时间范围，怎么办？
思考一下:

如果暴力，卡一下le和ri，随随便便让你O(n^2)T成狗。
用线段树或树状数组搞一搞,抱歉,这个复杂度是O(Qlogn)的,还是会T(虽然他们解决别的题目很NB)
差分,没错,就是标题，很高兴O(n)+常数…

方法

还是用上面这个题目,假如要在le和ri上全都加一个x,很显然,这个O(n)是不可避免的,既然这样,那我们考虑把O(n*Q)变成O(n+Q).也就是说,在询问中我们不去for来加x,而是做一个标记,最后一起加上。嗯，这里暂时记住就好…
现在需要自己动笔模拟一下了！
实现
先另外开一个专门差分的数组(大小=题中的序列长度)

假如在3~8的区间上加上5,那我们在差分数组中的3位置上加上一个5(原因暂时不懂没关系,用笔先跟着模拟),再在8+1的位置上减一个5,如此操作完Q次。

假如我们只有这一次操作,开始统计答案,运用前置和的思想,cfi=cf[i-1]+cf[i].那么你会发现(如果你模拟了的话),在3~8的区间上,你已经使差分数组全部加上了5(推广到所有Q一起统计答案依旧正确)

再用O(n)的for把他们加到原序列之中去,输出!

看一下复杂度,果然:O(常数*n).
这个代码应该不难,所以我也就不贴了(其实这算一种思想,没有完全的板子)

最后

加入自己的理解对知乎dl的文章小修了一下
https://zhuanlan.zhihu.com/p/25185969