ACM数据结构模板（更新ing...）

• 并查集
• KMP算法
• 树状数组
• 线段树
• 莫队算法

1、并查集

描述: 一种用来管理元素分组情况的数据结构。并查集可以高效的进行如下操作：

• 查询元素a和元素b是否属于同一个数组。
• 合并元素a和元素b所在的组。

代码:

// 并查集
int par[Max_n];  //父亲
int rank[Max_n]; //树的高度

void init(int n){ //初始化n个元素
    for(int i=0;i

**复杂度:**加入优化后效率非常高，对n个元素的元素进行一次操作的复杂度是O(α(n))，比O(logn)还要快。

2、KMP算法

描述: KMP算法是一种改进的字符串匹配算法，是利用匹配失败后的信息，尽量减少模式串与主串的匹配次数以达到快速匹配的目的，时间复杂度O(m+n)。

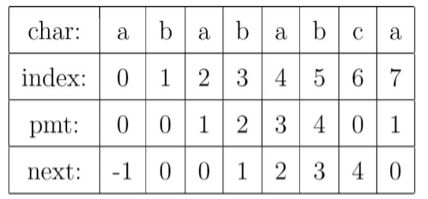
• pmt数组记录的是字符串前缀集合和后缀集合的最长匹配。为了编程的方便，不直接使用pmt数组，而pmt数组向后偏移一位得到next数组。即next数组 记录的是主串字符与模式串字符失配时，主串应与模式串的第next[j]个字符再进行比较。

代码:

next是C++中的保留字，使用next数组，会CE！

char s[Max_n],t[Max_n];
int next[Max_n];
int slen,tlen;

void getNext(){ //next数组
    int i=0,j=-1;
    next[0]=-1;
    while(i

next数组和优化后的next2数组：

3、树状数组

描述: 树状数组用来维护数组的前缀和，从而可以快速求得某一个区间的和，并支持对元素的值进行修改。但是树状数组并非只有这一种功能，变形后它还能衍生出两个功能，本文我们就来分别讨论下树状数组这三大功能。

永远要记住，基本的树状数组维护的是数组的前缀和，所有的区间求值都可以转化成用 sum[m]-sum[n-1] 来解，这点无论是在改点还是接下来要说的改段中都非常重要！

1.改点求段（单点修改 区间查询）

这也是树状数组的基本应用。我们可以来看一下这道题 敌兵布阵。
代码:

#include
#include
#include
#include
using namespace std;
typedef long long ll;
const int Max_n=1e5+10;

int t,n,k=0;
int c[Max_n];

int lowbit(int k){
    return k&-k;
}

void update(int k,int val){
    while(k<=n){
        c[k]+=val;
        k+=lowbit(k);
    }
}

int sum(int k){
    int ans=0;
    while(k>0){
        ans+=c[k];
        k-=lowbit(k);
    }
    return ans;
}

int main()
{
    scanf("%d",&t);
    while(t--){
        scanf("%d",&n);
        int a,b;
        char s[10];
        memset(c,0,sizeof(c));
        for(int i=1;i<=n;i++){
            scanf("%d",&a);
            update(i,a);
        }
        printf("Case %d:\n",++k);
        while(~scanf("%s",s)&&s[0]!='E'){
            if(s[0]=='Q'){
                scanf("%d%d",&a,&b);
                printf("%d\n",sum(b)-sum(a-1));
            }
            else if(s[0]=='A'){
                scanf("%d%d",&a,&b);
                update(a,b);
            }
            else {
                scanf("%d%d",&a,&b);
                update(a,-b);
            }
        }
    }
    return 0;
}

2.改段求点（区间修改 单点查询）

改段求点和改点求段恰好相反，比如有一个数组 a = [x, 0, 0, 0, 0, 0, 0, 0, 0, 0]，每次的修改都是一段，比如让 a[1]~a[5] 中每个元素都加上10，让 a[6]~a[9] 中每个元素都减去2，求任意的元素的值。

看例题： Color the ball

跟改点求段不同，这里要转变一个思想。在改点求段中，c[i]表示Ci节点所管辖的子节点的元素和，而在改段求点中，c[i]表示Ci所管辖子节点的批量统一增量。

还是看这个经典的图：

比方说，C8管辖A1_{A8这8个节点，如果A1}A8每个都染色一次，因为前面说了c[i]表示i所管辖子节点的统一增量，那么也就是 c[8]+=1，A5~A7都染色两次，也就是 c[6] +=2, c[7] +=2 。如果要求A1被染色的次数，C8是能管辖到A1的，也就是说c[8]的值和A1被染色的次数有关，仔细想想，也就是把能管辖到A1的父节点的c值累积起来即可。两个过程正好和改点求段相反。

代码:

#include
#include
#include
#include
using namespace std;
typedef long long ll;
const int Max_n=1e5+10;

int n;
int c[Max_n];

int lowbit(int k){
    return k&-k;
}

void update(int k,int val){
    while(k>0){
        c[k]+=val;
        k-=lowbit(k);
    }
}

int query(int k){
    int ans=0;
    while(k<=n){
        ans+=c[k];
        k+=lowbit(k);
    }
    return ans;
}

int main()
{
    while(~scanf("%d",&n)&n){
        memset(c,0,sizeof(c));
        int a,b;
        for(int i=0;i

3.改段求段（区间修改 区间查询）

改段求段也有道经典的模板题：A Simple Problem with Integers

我们还是从简单的例子入手，比如有数组a[10]={1,2,3…9}。

假设我们将 a[1]~a[4] 这段增加5，对于我们要求的区间和来说，要么是 [1,2] 这种属于所改段的子区间，要么是 [1,8] 这种属于所改段的父区间（前面说了，所有的区间求值都可以用sum[m]-sum[n-1]来解，所以我们只考虑前缀和），我们分别讨论。

1）如果所求是类似 [1,8] 这种，我们可以很开心地发现，我们将区间增量(4*5)全部加在 a[4] 这个元素上，对结果并没有什么影响！于是变成了一般的改点求段。

2）如果所求是类似 [1,2] 这种，我们可以用类似改段求点中染色的思想进行处理。譬如 [1,4] 成段加5，如果我们要计算 [1,2] 的和。我们将 [1,3] 进行“染色”（节点4加上了4*5的权重），因为 [1,3] 在树状数组的划分中可以分为两个区间，[1,2] 和 [3,3]，所以我们用类似改段求点对这两块区域进行“染色”，染上的次数为5。我们要求的是 [1,2] 的区间和，我们只需找 2 被染色的次数，因为 [1,n] 进行染色。如果m(1<=m<=n)被染色，那么m的左边肯定都被染色了。求出被染色的次数，然后乘上区间宽度，就是整段的和了。

这样我们分别对两种情况进行了处理，更重要的是，这两种情况互不影响！于是我们简单地把两个结果相加就ok了，而这两个过程，分别正是改点求段和改段求点！

#include
#include
#include
#include
using namespace std;
typedef long long ll;
const int Max_n=1e5+10;

int N,Q;
ll b[Max_n],c[Max_n];

int lowbit(int k){
    return k&-k;
}

void update_backward(int k,int val){ 
    while(k<=N){
        b[k]+=val;
        k+=lowbit(k);
    }
}

void update_forward(int k,int val){ 
    while(k>0){
        c[k]+=val;
        k-=lowbit(k);
    }
}

void update(int k,int val){
    update_backward(k,k*val);
    update_forward(k-1,val);
}

ll query_forward(int k){
    ll ans=0;
    while(k>0){
        ans+=b[k];
        k-=lowbit(k);
    }
    return ans;
}

ll query_backward(int k){
    ll ans=0;
    while(k<=N){
        ans+=c[k];
        k+=lowbit(k);
    }
    return ans;
}

ll query(int k){
    return query_forward(k)+k*query_backward(k);
}

int main()
{
    scanf("%d%d",&N,&Q);
    int x,y,z;
    char s[10];
    memset(b,0,sizeof(b));
    memset(c,0,sizeof(c));
    N+=1;  //下标2~n+1
    for(int i=2;i<=N;i++){
        scanf("%d",&x);
        update_backward(i,x);
    }
    for(int i=0;i

注意： 一般的用数组来解的题，都是不用a[0]的，也就是元素是从a[1]~a[n]。而本题中的改段求段中的元素是从 a[2]~a[n+1]，因为 update()更新区间[1,x]（x为任意值）时，左端点为0向后更新update_backward会造成死循环！

// 支持本小节树状数组原创作者：韩子迟，十分感谢~~

4、线段树

描述: 是一种树状结构来存储一个连续区间的信息的数据结构。线段树是平衡二叉树，所有操作都是logn级别，每个节点对应一个区间。关键的一点：需要维护哪些区间的附件信息，怎样维护这个信息。

代码风格：

1. 数组要开节点数Max_n的4倍，详见证明，lson和rson分别代表当前节点的左右儿子。
2. 函数传参时，同时传递当前儿子的节点rt和对应的区间[l,r]。
3. pushUP(int rt) 把当前结点的信息更新给父结点。
   pushDown(int rt) 把当前结点的信息更新给儿子结点。
4. 线段树维护的区间范围是[1,x]，根节点从1开始（1,2,3…）!!!

hdu-1166 敌兵布阵

• 简单的单点修改，区间查询

#include
#include
#include
#include
using namespace std;
#define lson l,m,rt<<1
#define rson m+1,r,rt<<1|1
const int Max_n=5e4+10;

int tree[Max_n<<2];

void pushUp(int rt){
	tree[rt]=tree[rt<<1]+tree[rt<<1|1];
}

void build(int l,int r,int rt){
	if(l==r){
		scanf("%d",&tree[rt]);
		return;
	}
	int m=(l+r)>>1;
	build(lson);build(rson);
	pushUp(rt);
}

void update(int k,int value,int l,int r,int rt){ //单点更新 
	if(l==r){
		tree[rt]+=value;
		return;
	} 
	int m=(l+r)>>1;
	if(k<=m)update(k,value,lson);
	else update(k,value,rson);
	pushUp(rt);
} 

int query(int L,int R,int l,int r,int rt){
	if(r<=R&&l>=L)return tree[rt];
	int ans=0;
	int m=(l+r)>>1;
	if(L<=m)ans+=query(L,R,lson);
	if(R>=m+1)ans+=query(L,R,rson);
	return ans; 
}

int main()
{
	int T,n;
	scanf("%d",&T);
	for(int i=1;i<=T;i++){
		printf("Case %d:\n",i);
		scanf("%d",&n); 
		build(1,n,1);
		char s[110];
		int x,y;
		while(~scanf("%s",s)&&s[0]!='E'){
			scanf("%d%d",&x,&y);
			if(s[0]=='A')update(x,y,1,n,1);
			else if(s[0]=='S')update(x,-y,1,n,1);
			else printf("%d\n",query(x,y,1,n,1));
		}
	}
	return 0;
}

poj 3468 A Simple Problem with Integers

• 区间修改，区间查询（lazy标记）
• lazy标记思想：更新到某个区间的时候，先给这个区间打上lazy标记，不去更新子区间。当下一次更新子区间的时候再把该区间的lazy标记更新到子区间。从而避免浪费更新那些不必要的结点的时间。

#include
#include
#include
#include
#define lson l,m,rt<<1
#define rson m+1,r,rt<<1|1
using namespace std; 
typedef long long ll;
const int Max_n=1e5+10;

int s[Max_n];
ll sum[Max_n<<2];
int lazy[Max_n<<2];

void pushUp(int rt){
	sum[rt]=sum[rt<<1]+sum[rt<<1|1];
}

void pushDown(int rt,int len){
	if(lazy[rt]){
		lazy[rt<<1]+=lazy[rt];
		lazy[rt<<1|1]+=lazy[rt];
		sum[rt<<1]+=(len-(len>>1))*lazy[rt];
		sum[rt<<1|1]+=(len>>1)*lazy[rt];
		lazy[rt]=0;
	}
}

void build(int l,int r,int rt){
	lazy[rt]=0;
	if(l==r){
		sum[rt]=s[l];
		return;
	}
	int m=(l+r)>>1;
	build(lson);build(rson);
	pushUp(rt);
}

void update(int L,int R,int c,int l,int r,int rt){
	if(l>=L&&r<=R){
		lazy[rt]+=c;
		sum[rt]+=(ll)c*(r-l+1);
		return;
	}
	int m=(l+r)>>1;
	pushDown(rt,r-l+1);
	if(L<=m)update(L,R,c,lson);
	if(R>=m+1)update(L,R,c,rson);
	pushUp(rt);
}

ll query(int L,int R,int l,int r,int rt){
	if(l>=L&&r<=R)return sum[rt];
	pushDown(rt,r-l+1);
	int m=(l+r)>>1;
	ll ans=0;
	if(L<=m)ans+=query(L,R,lson);
	if(R>=m+1)ans+=query(L,R,rson);
	return ans;
}

int main()
{
	int n,t;
	scanf("%d%d",&n,&t);
	for(int i=1;i<=n;i++)scanf("%d",&s[i]);
	build(1,n,1);
	char ch;
	int x,y,z;
	while(t--){
		cout<

5、莫队算法

描述： 一种优雅的暴力，离线处理一类区间不修改查询类问题的算法。通过预先知道所有的询问，合理的组织每个询问的顺序以此来降低复杂度。
复杂度： O(n*√n)

66666666666666666666666666