从分类任务中了解机器学习（《机器学习实战》笔记）

数据集

使用的数据集为MNIST，其数据集中一共包含70000个手写数字的图片以及相应的标签。书上提供的读取数据集的代码由于版本不匹配（当时的版本较老），无法执行。因此只能在网上下载MNIST数据集。读取的方法参考：读取MNIST。
具体的数据准备工作代码如下：

import scipy.io as sio

mnist = sio.loadmat("datasets/mnist-original.mat")
X,y = mnist["data"].T,mnist["label"].T
print(X.shape)
# (70000, 784)

之后我们使用matplotlib查看其中包含的图片：

import matplotlib.pyplot as plt
import matplotlib

%matplotlib inline

some_digit = X[36000]
some_digit_image = some_digit.reshape(28,28)
#将数据从一维的变为2维的

plt.imshow(some_digit_image,cmap=matplotlib.cm.binary,
          interpolation="nearest")

结果如下：

之后我们可以将数据分为训练集和测试集，并将测试集和测试集标签进行洗牌：

import numpy as np

shuffle_index = np.random.permutation(60000)
X_train,y_train = X_train[shuffle_index],y_train[shuffle_index]

至此，数据的准备已经完毕。

一个二元分类器

我们写一个区分5和非5的分类器来对分类任务进行说明，首先将标签进行更改，非5的标签改为False，5改为True：

y_train_5 = (y_train == 5).ravel()
y_test_5 = (y_test == 5)。ravel()
#将数据变为1维

我们使用**随机梯度下降（SGD）**分类器来作为初始的分类器，使用训练集来对其进行训练：

from sklearn.linear_model import SGDClassifier

sgd_clf = SGDClassifier(random_state=42)
sgd_clf.fit(X_train,y_train_5)

这样，经过训练好的SGD分类器就可以根据输入的数字图片来判断该数字是否是5。

性能评估

交叉验证评估精度

我们可以使用交叉验证来查看训练好的分类器的精度：

from sklearn.model_selection import cross_val_score
# 3折
cross_val_score(sgd_clf,X_train,y_train_5,cv=3)
# array([0.9603 , 0.9606 , 0.96895])

可以看出其分类精度达到了95%以上，但是这并不是说这个分类器很优秀，因为非5的样本数比5的样本数多许多（也就是说一直瞎猜非5，也可以达到90%的准确率），这就是所谓的倾斜数据集。

混淆矩阵

在分类问题中混淆矩阵可以展示A类正确分类、分入B类、B类正确分类、分入A类的样例数（在这个实例中，是5被正确分至5类，被错误分到非5类、0-4,6-9被正确分入非5类，被错误分入5类的数量）。
在获得混淆矩阵之前，我们首先需要得到模型对训练集的预测结果，我们可以使用cross_val_predict()函数，它与cross_val_score()函数类似，使用交叉验证的方式对模型进行训练评估，但是返回的是每组的预测结果，然后我们使用confusion_matrix来获取混淆矩阵：

from sklearn.model_selection import cross_val_predict
from sklearn.metrics import confusion_matrix

sgd_clf = SGDClassifier(random_state=42)
y_train_pred = cross_val_predict(sgd_clf,X_train,y_train_5,cv=3)
confusion_matrix(y_train_5,y_train_pred)
# array([[53748,   831],
#        [ 1372,  4049]], dtype=int64)

矩阵的左上角是被正确分类至非5的样例数（真负类），右上角是5被错误分至5的样例数（假正类），左下角是被错误分至非5的样例数（假负类），右下角则是正确被分至5的样例数（真正类）。
混淆矩阵可以提供大量的信息，首先是正类预测的准确率，也称为精度，其定义为：$$精度=\frac{TP}{TP+FP}$$
其中TP为真正类的样例数，FP为假正类的样例数。
另外一个分类器的指标就是召回率，也称为灵敏度，它代表了分类器检测到的真正类的比率：$$召回率=\frac{TP}{TP+FN}$$
其中FN是假负类的数量。

精度和召回率

使用sklearn中的函数可以轻松的计算精度和召回率：

from sklearn.metrics import precision_score,recall_score,f1_score

print(precision_score(y_train_5,y_train_pred))
# 精度
# 0.8297131147540984
print(recall_score(y_train_5,y_train_pred))
# 召回率
# 0.6731230400295148
f1_score(y_train_5,y_train_pred)
# 0.74997430890967
# F1分数

从准确率和召回率来看，这个模型的性能并没有想象中的好。
对于分类器来说，我们可以将其准确率和召回率来进行组合，形成一个新的最后一行代码计算的指标叫做F1分数，其定义为：$$F_1=\frac{2}{\frac{1}{精度}+\frac{1}{召回率}}=2\times \frac{精度\times 召回率}{精度+召回率}=\frac{TP}{TP+\frac{FN+FP}{2}}$$
只有当分类器的精度和召回率都较高的时候，分类器才能得到较高的F1分数，当分类器具有相近精度和召回率的时候得分较高，对于不同的情况我们衡量分类器的指标也不同。
对于一个模型，不能同时增加精度和召回率，当提升一个指标的时候，另外一个指标会发生下降，这个现象称为精度/召回率权衡。

精度/召回率权衡

对于SGD分类器，其原理是计算出一个分数，当分数大于给定的阈值，则判定为为真正类，否则视为假负类。一般情况下，我们可以提高阈值来增加精度，但是召回率一般会随之下降。我们可以使用precision_recall_curve()来查看阈值与精度、召回率的关系：

from sklearn.metrics import precision_recall_curve

def plot_precison_recall_vs_threshold(precisions,recalls,thresholds):
    """
    用于阈值、精度和召回率关系的可视化
    """
    plt.plot(thresholds,precisions[:-1],"b--",label="precisions")
    plt.plot(thresholds,recalls[:-1],"g--",label="recalls")
    plt.xlabel("thresholds")
    plt.legend(loc="upper left")
    plt.ylim([0,1])

#"decision_function"表示返回的是每一个样本所得到的分数
y_scores = cross_val_predict(new_sgd_clf,X_train,y_train_5,cv=3,
                            method="decision_function")
precisions,recalls,thresholds = precision_recall_curve(y_train_5,y_scores)

#绘制曲线
plot_precison_recall_vs_threshold(precisions,recalls,thresholds)
plt.show()

结果如下：

可以看出随着阈值的上升，其精度可能会出现一个局部的下降，但是总体来说会呈上升的趋势。我们还可以绘制出精度/召回率的曲线：

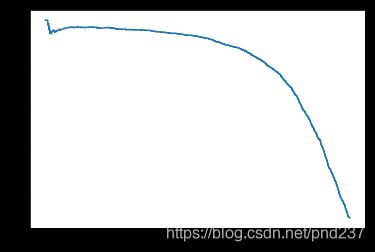
一般来说其曲线越接近右上角代表分类器性能越优秀。

ROC曲线

受试者工作特征曲线（ROC曲线）与精度/召回率曲线非常相似，但是他是真正类率（召回率，TPR）和假正类率的关系（FPR）的关系。绘制ROC曲线，我们首先需要计算不同阈值情况下的TPR和FPR，之后将其使用matplotlib进行可视化：

from sklearn.metrics import roc_curve

def plot_roc_curve(fpr,tpr,label=None):
    plt.plot(fpr,tpr,linewidth=2,label=label)
    plt.plot([0,1],[0,1],'k--')
    plt.axis([0,1,0,1])
    plt.xlabel("False Positive Rate")
    plt.ylabel("True Positive Rate")
    
fpr,tpr,thresholds = roc_curve(y_train_5,y_scores)
plot_roc_curve(fpr,tpr)
plt.show()

一个分类器越是优秀，其ROC曲线却接近左上角，另外我们还可以计算其ROC曲线的下面积（AUG）来比较分类器的性能，完美的分类器ROC AUG等于1，而随机的分类器ROC AUG为0.5:

from sklearn.metrics import roc_auc_score
roc_auc_score(y_train_5,y_scores)
# 计算下面积
# 0.9658586784598172

关于ROC曲线与精度/召回率曲线的选择：正类非常少见的时候或者更加关注假正类而不是假负类的时候，应该选择精度/召回率曲线，反之则是ROC曲线。
我们还可以训练一个随机森林分类器，比较两者的ROC曲线和ROC AUG。另外，由于这个分类器没有decision_function()，即无法获取每个实例的分数，但是他有dict_prob()方法，可以给定属于某个类别的概率，在这个问题中，0.7代表该数字有百分之七十的概率是5。由于没有分数，我们将正类的概率视为分数，来绘制ROC曲线：

from sklearn.ensemble import RandomForestClassifier

forest_clf = RandomForestClassifier(random_state=42)
y_probas_forest = cross_val_predict(forest_clf,X_train,y_train_5,cv=3,
                                   method="predict_proba")
#返回每一个实例为5的概率

y_scores_forest = y_probas_forest
fpr_forest,tpr_forest,thresholds_forest = roc_curve(y_train_5,y_scores_forest)

# 可视化
plt.plot(fpr,tpr,"b:",label="SGD")
plot_roc_curve(fpr_forest,tpr_forest,"Random Forest")
plt.legend(loc="lower right")
plt.show()

roc_auc_score(y_train_5,y_scores_forest)
# 随机森林选择器的下面积
# 0.9984388153827978

多类别分类器

多类别分类器（也称为多项分类器）可以区分两个以上的类别。某些算法可以直接处理多个类别的分类（如随机森林分类器以及朴素贝叶斯分类器）；也有一些分类器只能处理二分类的问题（如支持向量机分类器和线性分类器），对于这些分类器，我们可以将多个分类器组合，使其可以完成多分类任务，组合的方式一般由两种：

• 一对多（OvA）策略，若有n个类别则需要n个分类器，比如MNIST分类，需要10个分类器，分别用于识别0，1，2，……，9，当有一张图片需要识别的时候，将图片直接输入到10个分类器之中，哪个分类器给的分数高，就属于哪一类。
• 多对多（OvO）策略，若有n个类别则需要n(n-1)/2个分类器（相当于$C_n^2$），对于本例，则需要45个分类器，用于去区分任意两个数字，即$C_{10}^2$。将数据输入后，看哪一个类别获胜的次数多，则将其归为某一类。该方法有一个优点，那就是在训练时，某一个分类器的训练数据仅仅包含相应两个类别的数据。

*对于两种策略的说明：*对于大部分二元分类器，OvA策略是一个比较好的选择。但是对于某些二元分类器（如支持向量机）在数据量非常大的情况下训练会非常慢，此时建议选择OvO策略。

在sklearn中，如果使用二元分类器去执行多分类任务，它会自动运行OvA模式（SVM分类器为OvO），比如SGD分类器：

sgd_clf = SGDClassifier(random_state=42)
sgd_clf.fit(X_train,y_train) #z这里是y_train，包含所有数字的标签
some_digit_scores = sgd_clf.decision_function([X_train[36000]])
# 会显示出所有分类器的得分，将其归为分数高的那一类

这里默认的使用的是OvA策略，如果想要使用OvO策略，则需要导入OneVsRestClassifier类，将我们的分类器传递给它的构造函数：

from sklearn.multiclass import OneVsOneClassifier
ovo_clf = OneVsOneClassifier(SGDClassifier(random_state=42))
ovo_clf.fit(X_train,y_train)
ovo_clf.predict([X_train[36000],X_train[36001]])

对于随机森林分类器，则直接将训练集和标签传入即可，其预测结果是一个Numpy数组，值表示属于该类的可能性：

forest_clf = RandomForestClassifier(random_state=42)
forest_clf.fit(X_train,y_train)
forest_clf.predict([X_train[36000],X_train[36001]])
forest_clf.predict_proba([X_train[digit_a],X_train[digit_b]])
# array([[0.03, 0.  , 0.07, 0.01, 0.72, 0.01, 0.08, 0.03, 0.  , 0.05],
#        [0.  , 0.01, 0.  , 0.05, 0.01, 0.86, 0.  , 0.  , 0.07, 0.  ]])

对于这个分类器，我们可以使用交叉验证的方法来验证其准确性，另外为了提高准确率，可以在训练之前将数据标准化：

from sklearn.model_selection import cross_val_score
from sklearn.preprocessing import StandardScaler

#标准化
scaler = StandardScaler()
X_train_scaled = scaler.fit_transform(X_train)

#训练，可能时间比较长
sgd_clf = SGDClassifier(random_state=42)
cross_val_score(sgd_clf,X_train_scaled,y_train,cv=3,scoring="accuracy")
# array([0.90045, 0.8979 , 0.90075])

错误分析

对于之前的多分类器，我们也可以查看其混淆矩阵：

from sklearn.metrics import confusion_matrix
from sklearn.model_selection import cross_val_predict

y_train_pred = cross_val_predict(sgd_clf,X_train_scaled,y_train,cv=3)
# 交叉验证，得出预测结果

conf_mx = confusion_matrix(y_train,y_train_pred)
print(conf_mx)
# array([[5583,    0,   17,    8,    7,   36,   34,    4,  233,    1],
#        [   1, 6422,   43,   24,    3,   43,    5,    9,  183,    9],
#        [  24,   25, 5257,   91,   69,   20,   69,   36,  359,    8],
#        [  26,   19,  112, 5222,    3,  204,   28,   41,  415,   61],
#        [  10,   15,   40,    8, 5236,   11,   37,   21,  315,  149],
#        [  26,   18,   28,  155,   58, 4454,   77,   21,  521,   63],
#        [  27,   20,   49,    2,   46,   86, 5547,    5,  136,    0],
#        [  18,   13,   52,   22,   48,   14,    4, 5703,  184,  207],
#        [  15,   59,   41,   89,    2,  127,   30,    9, 5434,   45],
#        [  23,   24,   31,   58,  133,   33,    1,  168,  354, 5124]],
#       dtype=int64)

由于数字太多，混淆矩阵看上去并不直观，因此我们可以将矩阵可视化，即数字越小的地方颜色越深，数字越大的地方颜色越浅：

import matplotlib.pyplot as plt

%matplotlib inline

plt.matshow(conf_mx,cmap=plt.cm.gray)
plt.show()

结果如下：

另外我们可以看一下每种分类错误的错误率：

row_sums = conf_mx.sum(axis=1,keepdims=True)
# 按列相加，求出一种数字的数据量
norm_conf_mx = conf_mx / row_sums
# 求出错误率

np.fill_diagonal(norm_conf_mx,0)
#关心的是错误率，将对角线替换为0
plt.matshow(norm_conf_mx,cmap=plt.cm.gray)
plt.show()

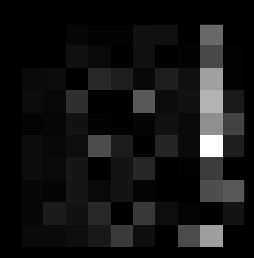
颜色越浅，则说明错误率越高，对于上面的这个混淆矩阵，可以看出其第5行第8列非常的亮，这说明数字5非常容易被错误归类为8。另外第8列总体较亮，说明各个数字都容易被错误的认为是数字8。

多标签分类

有时候，我们的数据可能不仅仅只有一个标签，比如对于数字9，它既是一个大于7的数字，也是一个奇数。这种输出的结果是一个二元标签的分类器称为多标签分类系统。
举一个例子，使用K近邻算法找到大于等于7并且是奇数的数字：

from sklearn.neighbors import KNeighborsClassifier

y_train_large = (y_train >= 7)
#标签1 大于等于7的数
y_train_odd = (y_train % 2 ==1)
#标签2 奇数
y_multilabel = np.c_[y_train_large,y_train_odd]
#合并

knn_clf = KNeighborsClassifier()
knn_clf.fit(X_train,y_multilabel)

knn_clf.predict([X_train[digit_a]]) #预测
#array([[False, False]])

多输出分类

多输出分类可以理解为输出了很多标签的分类器，比如一个去除图片噪声的分类器，输入的是夹杂噪声的图片，输出的则是去掉噪声的图片，标签则是图片中的所有像素（此时分类和回归之间的界限似乎非常模糊）。
下面是去除随机噪声的多输出分类器的小实例：

import matplotlib

def plot_digit(some_digit):
    """
    用于打印数据集中的数字图片
    """
    some_digit_image = some_digit.reshape(28,28)
    plt.imshow(some_digit_image,cmap=matplotlib.cm.binary,
              interpolation="nearest")
    plt.axis("off")
    plt.show()

noise1 = np.random.randint(0,100,(len(X_train),784))
# 加在训练集上的噪声
noise2 = np.random.randint(0,100,(len(X_test),784))
# 加在测试集上的噪声

# 噪声与图片混合
X_train_mod = X_train + noise1
X_test_mod = X_test + noise2

#原图片作为标签
y_train_mod = X_train
y_test_mod = X_test

knn_clf.fit(X_train_mod,y_train_mod)

clean_digit = knn_clf.predict([X_test_mod[2122]])
# 打印夹杂噪声的图片以及去噪声后的图片
plot_digit(X_test_mod[2122])
plot_digit(clean_digit)

下面是结果：