ADJUSTED BOXPLOT: 偏态分布的异常检测

Boxplot是一个常用的了解数据分布的工具，在数据预处理阶段也常用boxplot剔除离群点，但是当数据是一个偏态分布的时候，boxplot将许多点误分类为离群点。《AN ADJUSTED BOXPLOT FOR SKEWED
DISTRIBUTIONS》是一篇经典的修正boxplot在偏态分布数据上的误报问题的文章。

1. 传统boxplot方法

对于一组数据$X_n=\{x_1,x_2,x_3,...,x_n\}$，计算Q1(第一四分位数), Q3(第三四分位数), IQR(四分位距)，然后得到Tukey bound：
$$[Q_1-1.5\ast IQR,Q_3+1.5\ast IQR]$$
boxplot 方法认为落在tukey bound外的数据为离群值。

缺点：该上下界是基于数据时对称分布得到的，当数据是偏态分布时tukey bound表现得并不好。

2. 通用的boxplot方法

medcouple

medcouple(MC)是一个健壮的，用于描述连续单变量分布(F)偏度的统计量：
$$MC(F)=\underset{x_i<m_F<x_j}{\mathrm{median}}h(x_i,x_j)$$

$m_F$是F的中值，$x_i,x_j$是F中的样本，核函数h(x)定义如下：
$$h(x_i,x_j)=\frac{(x_j-m_F)-(m_F-x_i)}{x_j-x_i}$$
MC取值在[-1,1]，MC>0分布右偏，MC<0分布左偏。对于对称分布，MC=0。

boxplot修正

接下来利用MC对tukey bound进行偏态修正，这里引入修正函数$h_l(MC)$和$h_r(MC)$：
$$[Q_1-h_l(MC)\ast IQR,Q_3+h_r(MC)\ast IQR]$$
这里需要满足$h_l(0)=h_r(0)=0$，以保证和原始boxplot在对称分布数据中取得同样的效果。

然后作者研究了3种简单的，不需要太多参数的关于修正函数的模型：

1. 线性模型：$h_l(MC)=1.5+a\ast MC$, $h_r(MC)=1.5+b\ast MC$
2. 二次多项式模型：$h_l(MC)=1.5+a_1\ast MC+a_2\ast M{C}^2$, $h_r(MC)=1.5+b_1\ast MC+b_2\ast M{C}^2$
3. 指数模型：$h_l(MC)=1.5\ast e^{a\ast MC}$, $h_r(MC)=1.5\ast e^{b\ast MC}$

为了求上述模型中的常数，我们要求离群值的期望百分比为0.7%，这与正态分布下原箱线图的离群值百分比一致。

以线性模型举例，常数a,b应该满足$Q_1-(1.5+a\ast MC)\ast IQR=Q_{\alpha }$,$Q_3+(1.5+b\ast MC)\ast IQR=Q_{\beta }$，其中$Q_p$表示分布中的第p分位数，$\alpha =0.0035,\beta =0.9965$。线性模型的修正函数可以改写为：$\frac{Q_1-Q_{\alpha }}{IQR}-1.5=a\ast MC$和$\frac{Q_{\beta }-Q_3}{IQR}-1.5=b\ast MC$，然后可以用无截距的线性回归估计常数a和b。

二次模型和指数模型也可以利用同样的推导方法进行估计。例如，对于指数模型，经过转换，得到下面的线性形式：
$$\begin{gathered} ln(\frac{2}{3}\frac{Q_1-Q_{\alpha }}{IQR})=a\ast MC \\ ln(\frac{2}{3}\frac{Q_{\beta }-Q_3}{IQR})=b\ast MC \end{gathered}$$

然后，作者从$\Gamma ,{\chi }^2,F,Pareto,G_g$分布族中衍生出12605个分布的数据，用于训练出参数a,b。分布选取不极端倾斜的分布（保证medcouple<=0.6，因为很难找到简单的模型解决极端分布的情况），每个分布生成了10000个观测值。最终结果如下（这里只考虑对称和右偏的分布，y轴为$ln(\frac{2}{3}\frac{Q_{\beta }-Q_3}{IQR})$）：

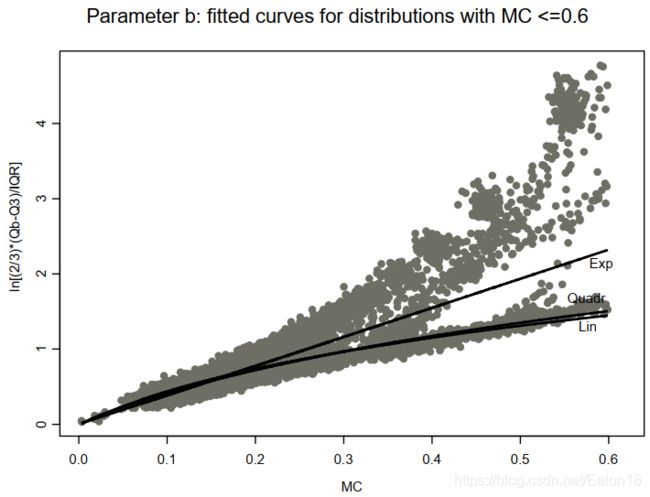
可以看到指数模型拟合效果最好。

最终修正后的上下界为：
$$[Q_1-1.5\ast e^{-3.5\ast MC}\ast IQR,Q_3+1.5\ast e^{4\ast MC}\ast IQR]$$

3. 总结

本文提出了一种进行偏度调整后的boxplot法，减弱了分布偏度的影响，在异常处理时是个不错的选择。

参考

[1]