单目三维运动重建（sfm算法）

算法介绍

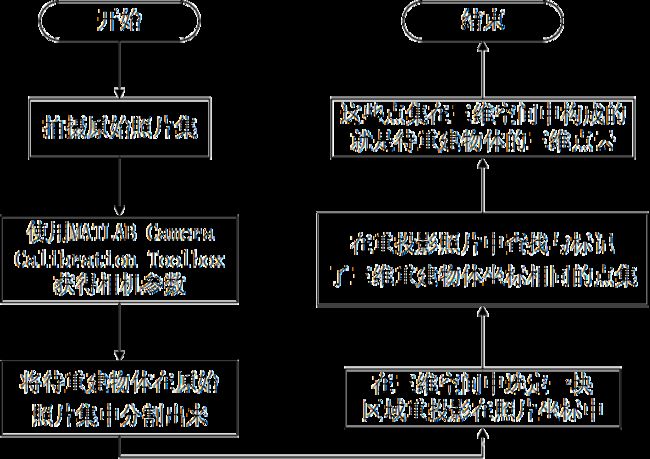
单目相机三维重建可以使用运动重建Structure from motion(SfM)方法，即由图像生成三维点云以及相机姿态。SfM方法的主要流程如图所示1，第一步，使用同一相机的从不同位置和姿态拍摄需要重建的物体，本实例为了简化后续操作在拍摄被重建物体同时也拍摄了标准标定板，如图2所示，得到原始照片集；第二步，使用MATLAB Camera Calibration Toolbox获得相机参数CameraParams，其中包括了相机的内参矩阵K，相机与标定照片的角度转移矩阵和位置转移矩阵；然后，使用图像分割方法将待重建物体在照片中标记出来并二值化，得到；接下来，选定空间中包含待重建物体的一块区域，使用第二步得到的相相机参数CameraParams，将三维空间利用成像原理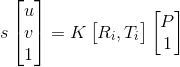重投影到照片坐标中得到重投影坐标；最后，在M中查找与中标记了三维重建物体像素坐标相同的点集，这些点对应的三维点云图就是待重建物体的点云。

算法流程图

 

包含待重建物体和标准标定板的照片

待重建物体分割效果图

重投影效果图

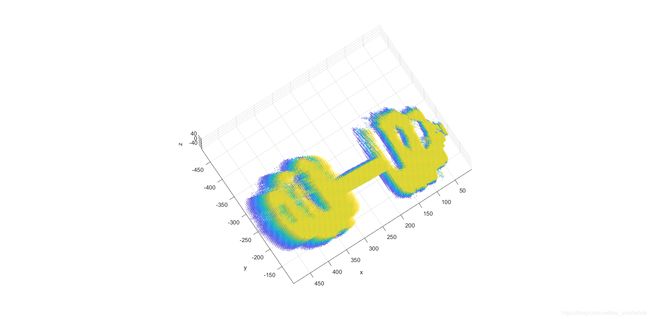三维重建效果图2

close all;
clear;
clc;

%% 1.Prepare Calibration Images
% Create a cell array of file names of calibration images.
numImages = 11;
files = cell(1, numImages);
for i = 1 : numImages
    eval(sprintf('files{%d} = ''d%d.jpg'';', i, i));
end

% Display one of the calibration images
I = imread(files{1});

%% 2.Estimate Camera Parameters

% Detect the checkerboard corners in the images.
[imagePoints, boardSize] = detectCheckerboardPoints(files);

% Generate the world coordinates of the checkerboard corners in the
% pattern-centric coordinate system, with the upper-left corner at (0,0).
squareSize = 47; % in millimeters
worldPoints = generateCheckerboardPoints(boardSize, squareSize);

% Calibrate the camera.
imageSize = [size(I, 1), size(I, 2)];
cameraParams = estimateCameraParameters(imagePoints, worldPoints, ...
   'ImageSize', imageSize);

% load('cameraParams.mat');

%% 3.待重建物体分割
label_images = cell(1, numImages);
for i = 1 : numImages
    originalImage = imread(files{i});
    originalImage = rgb2hsv(originalImage);
    originalImage = originalImage(:, :, 2) < 0.35 & ...
        originalImage(:, :, 3) < 0.15;
    undistortedImage = undistortImage(originalImage, cameraParams);
    label_images{i} = undistortedImage;
    [row, col] = size(label_images{i});
    % figure(), imshow(label_images{i});
    % pause(1);
end
%% 4.产生一个长方体点阵框住物体
step = 3;
x1 = -50; x2 = 600;
y1 = -500; y2 = -50;
z1 = -50; z2 = 50;
[x, y, z] = meshgrid(x1: step: x2, y1: step: y2, z1: step: z2);
num_points = length(x(:));
object = [x(:), y(:), z(:), ones(num_points, 1)];

%% 5.计算点阵在原图中的投影
flag = zeros(num_points, 1);
K = cameraParams.IntrinsicMatrix;
for j = 1 : numImages
    R = cameraParams.RotationMatrices(:,:,j);
    T = cameraParams.TranslationVectors(j,:);
    p_uv1 = object * [R;T] * K;
    s = p_uv1(:,3);
    p_uv = [p_uv1(:,1)./s, p_uv1(:,2)./s];  
    
    % 索引像素时，先行(y)后列(x)
    p_row = round(p_uv(:,2));
    p_col = round(p_uv(:,1));
    err_points = length( find( p_row <=0 ...
        | p_row>row | p_col <=0 | p_col > col ) );
    ind = p_row + (p_col-1)*row;
    ind(find(ind > size(label_images{j}, 1) * size(label_images{j}, 2))) = 1;
    ind(find(ind < 1)) = 1;
    flag = flag | label_images{j}(ind) > 0;

    % 显示投影效果
    if 1
        figure;imshow(label_images{j});
        hold on;
        indices = find(flag);
        p_uv_remain = p_uv(indices(1:5:end),:);
        plot(p_uv_remain(:,1),p_uv_remain(:,2),'r.');
        hold off;
    end
end

%% 6.重投影效果展示
object = object(flag,:);
figure; 
hold on;
[n,~] = size(object);
plot3(object(:,1), object(:,2), -object(:,3),'y.');
axis square;
hold off;
figure; pcshow([object(:,1), object(:,2), -object(:,3)]);
xlabel('x');
ylabel('y');
zlabel('z');
beep;