习题解答——姜启源《数学模型》

1 建立数学模型

1.3 包饺子

• 复习题二

  • 假设饺子越大面皮越厚，并且成正比例关系，即

    \[\begin{align*} SH &= n(sh) \\ H &= a h \end{align*} \]

    由此可以得到大饺子和小饺子的面皮面积满足

    \[S = \frac{n}{a}s \]

    根据教材中的中间结论

    \[\begin{align*} V &= kS^{\frac{3}{2}},& v =ks^{\frac{3}{2}} \end{align*} \]

    可以得到饺子馅体积的关系满足

    \[V = (\frac{n}{a})^{\frac{3}{2}}v = \sqrt{\frac{n}{a^3}}(nv) \]

    显然，在这个新的 \(V-nv\) 关系中，“饺子数量减少一倍能多包多少馅”的回答是与厚度变化系数\(a\)相关的：

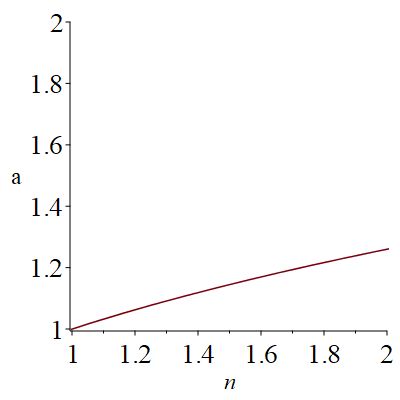
    1. 当\(a = \sqrt[3]{2} \approx 1.26\)时，能包的馅数量不变；
    2. 当\(a > 1.26\)时，能包的馅变少；
    3. 当\(a<1.26\)时，能包的馅增加。

    可以发现，厚度变化系数 \(a\) 存在一个临界值 \(\sqrt[3]{n}\) ，当它大于临界值时，能包的馅反而少了，反之则会更多。为了更好地观察这一临界值的变化，我们可以作出饺子数量变化倍数\(n\)与\(a\)临界值的关系图：

    

2 初等模型

2.2 滑艇比赛的成绩

复习题

考虑八人艇分重量组（桨手体重不超过86 kg）个轻量级组（桨手体重不超过73 kg），建立模型说明重量组的成绩比轻量组的大约好 5%.

考虑艇重

使用与书中相同的假设。

根据桨手输出的功率与阻力 \(f\) 和速度 \(v\) 的乘积成正比，有

\[\begin{equation} np \propto fv \label{2.2.1} \end{equation} \]

根据假设2，3，可得

\[\begin{align} f &\propto sv^2 &p \propto w \end{align} \]

代入\(\eqref{2.2.1}\)式，可得

\[\begin{equation} v \propto (\frac{nw}{s})^\frac{1}{3} \label{2.2.3} \end{equation} \]

教材中已经得到浸没面积 \(s\) 与艇手数 \(n\) 的关系

\[\begin{equation} s \propto n^\frac{2}{3} \label{2.2.2} \end{equation} \]

加入艇手体重和艇重，式\(\eqref{2.2.2}\)进一步写为

\[s \propto (kn+nw)^\frac{2}{3} \]

其中，\(k\) 是艇重与艇手数的比例系数.

代入\(\eqref{2.2.3}\)式，并考虑到同为八人艇，消去 $ n$，可以得到速度与艇手重量 \(w\) 的关系

\[v \propto \frac{w^\frac{1}{3}}{(w+k)^\frac{2}{9}} \]

因为比赛成绩 \(t\) 与 \(v\) 成反比，所以

\[\begin{equation} t \propto \frac{(w+k)^\frac{2}{9}}{w^\frac{1}{3}}\propto(\frac{1}{w}+\frac{2k}{w^2}+\frac{k^2}{w^3})^\frac{1}{9} \label{2.2.4} \end{equation} \]

由表1中最后一列的数据可知，对于八人艇，\(w_0=14.7n\)，即\(k=14.7\). 代入\(\eqref{2.2.4}\)式，可得

\[t \propto(\frac{1}{w}+\frac{29.4}{w^2}+\frac{216.09}{w^3})^\frac{1}{9} \]

最终，可以得到重量组和轻量组的相对成绩差为

\[\delta = \frac{t_{73}-t_{86}}{t_{73}} \approx 2.4\% \]

不考虑艇重

使用与书中相同的假设。

根据桨手输出的功率与阻力 \(f\) 和速度 \(v\) 的乘积成正比，有

\[\begin{equation} np \propto fv \label{2.2.5} \end{equation} \]

根据假设2，3，可得

\[\begin{align} f &\propto sv^2 &p \propto w \end{align} \]

代入\(\eqref{2.2.5}\)式，可得

\[\begin{equation} v \propto (\frac{nw}{s})^\frac{1}{3} \end{equation} \label{2.2.7} \]

教材中已经得到浸没面积 \(s\) 与艇手数 \(n\) 的关系

\[\begin{equation} s \propto n^\frac{2}{3} \end{equation} \label{2.2.6} \]

加入艇手体重和艇重，\(\eqref{2.2.6}\)式进一步写为

\[s \propto (nw)^\frac{2}{3} \]

代入\(\eqref{2.2.7}\)式，并考虑到同为八人艇，消去 $ n$，可以得到速度与艇手重量 \(w\) 的关系

\[v \propto w^\frac{1}{9} \]

因为比赛成绩 \(t\) 与 \(v\) 成反比，所以

\[t \propto w^{-\frac{1}{9}} \]

最终，可以得到重量组和轻量组的相对成绩差为

\[\delta = \frac{73^{-\frac{1}{9}} - 86^{-\frac{1}{9}}}{73^{-\frac{1}{9}}} \approx 1.8 \% \]

2.5 估计出租车的总数

复习题1

• MATLAB程序代码

  % estimate population with sample
  % based on 5 models, which are mean model, middle model, ends-symmeric
  % model, average interval model and average division model
  
  % 1. set parameters
  Population = 1:1000;
  n = 20;     %number of sample points
  m = 400;    %repeat 400 times
  
  % set models
  mMean =     @(sample)   2 * mean(sample) - 1;
  mMiddle =   @(sample)   2 * median(sample) - 1;
  mEndsSym =  @(sample)   max(sample) + min(sample) - 1;
  mAvInter =  @(sample)   (1+1/n)*max(sample) - 1;
  mAvDiv =    @(sample)   (1 + 1/(2*n-1))*(max(sample) - 1/(2*n));
  
  % initialize arrays for storing estimations
  eMean = zeros(1,m);
  eMiddle = zeros(1,m);
  eEndsSym = zeros(1,m);
  eAvInter = zeros(1,m);
  eAvDiv = zeros(1,m);
  
  % 2. generate results
  for i = 1:m
      sample = randi(1000, [1,n]);
      eMean(i) = mMean(sample);
      eMiddle(i) = mMiddle(sample);
      eEndsSym(i) = mEndsSym(sample);
      eAvInter(i) = mAvInter(sample);
      eAvDiv(i) = mAvDiv(sample);
  end
  
  %3. Analyze
  Mean = myAnalyze(eMean);
  Middle = myAnalyze(eMiddle);
  EndsSym = myAnalyze(eEndsSym);
  AvInter = myAnalyze(eAvInter);
  AvDiv = myAnalyze(eAvDiv);
  
  format bank;
  StatisticalFeatures = {'Mean';'Error';'Std'};
  result = table(StatisticalFeatures, Mean, Middle, EndsSym, AvInter, AvDiv)
  
  function result = myAnalyze(e)
      result = zeros(3,1);
      result(1) = mean(e);
      result(2) = result(1) - 1000;
      result(3) = std(e);
      
      result = round(result*100)/100;
  end
  

• 运行结果

  	Mean	Middle	EndsSym	AvInter	AvDiv
  'Mean'	1002.24	1002.93	998.22	1000.57	978.31
  'Error'	2.24	2.93	-1.78	0.57	-21.69
  'Std'	132.22	213.22	69.1	49.84	48.68

• 分析

  • 当\(m\)，\(n\) 增大时，主要有以下影响：
  1. 各个模型的误差都变小了，标准差的也减小了一些；
  2. 平均间隔模型的优越性更加突出地显现了出来。

2.8 核军备竞赛

复习题1

\[\begin{equation} y = \frac{y_0}{s^a}=\frac{y_0}{s^{x/y}},0

证明\(\eqref{2.8.1}\)具有以下性质：

1. 图线上凸
2. 若威慑值 \(y_0\) 变大，则曲线整体上移，且变陡
3. 若残存率 \(s\) 变大，则曲线变平

性质一：

由\(\eqref{2.8.1}\)可得到 \(x\) 的表达式

\[x={\frac {y}{\ln \left( s \right) }\ln \left( {\frac {y_{{0}}}{y}} \right) } \]

进一步地，可以求出其一阶导数和二阶导数

\[\begin{equation} x' = - \frac{1} {\ln \left( s \right)} +{\frac {1}{\ln \left( s \right) }\ln \left( {\frac {y_{{0}}}{y}} \right) } \end{equation} \label{2.8.2} \]

\[\begin{equation} x''=-{\frac {1}{y\ln \left( s \right) }} \end{equation} \label{2.8.3} \]

已知 \(0，故

\[\frac{1}{\ln(s)} <0 \]

由假设可知，\(y_0 < y\)，故

\[\ln(\frac{y_0}{y}) <0 \]

将上两式代入\(\eqref{2.8.2}\)和\(\eqref{2.8.3}\)，可得

\[x'>0 \]

\[x''<0 \]

所以 \(x\)-\(y\) 图线是下凹的，则可知 \(y\)-\(x\) 图线是上凹的.

性质二：

由 \(y_0\) 的代数含义可知，当 \(y_0\) 增大时，图线上移.

由\(\eqref{2.8.2}\)可知，当 \(y_0\) 增大时，\(x\) 的一阶导数变小，\(x\)-\(y\) 图线是变平的，则可知 \(y\)-\(x\) 图线是变陡的.

性质三：

由\(\eqref{2.8.2}\)可知，当 \(s\) 增大时，\(x\) 的一阶导数变大，\(x\)-\(y\) 图线是变陡的，则可知 \(y\)-\(x\) 图线是变平的.

证明完毕.

第 2 章训练题

第2题：请你设计按照测量长度估计鱼的质量的方法. 假定鱼池中只有一种鲈鱼，并且得到8条鱼的如下数据（胸围指鱼身的最大周长）：

身长/cm	36.8	31.8	43.8	36.8	32.1	45.1	35.9	32.1
质量/g	765	482	1162	737	482	1389	652	454
胸围/cm	24.8	21.3	27.9	24.8	21.6	31.8	22.9	21.6

先用机理分析建立模型，再用数据确定参数.

问题分析

题中提供的测量长度分别为鱼身的长度和最大周长。基于日常生活中对鲈鱼的观察，我们可以将鲈鱼视为一个类圆柱体，其体积由等效高与等效底面周长来确定。同时，类圆柱体的等效高与等效底面周长分别与测量数据成正比例关系。在建立起测量长度与鲈鱼体积的关系后，我们来考察鲈鱼体积与质量的关系。考虑到鱼池中只有一种鲈鱼，并且被测量的鱼都是成年鱼（这一点可以从身长中推测出），我们不妨假设该鱼池中所有成年鲈鱼的密度相同。这样鲈鱼的体积与质量也成一致的正比例关系。

下面将建立模型并使用数据来确定参数.

模型假设

计鱼身长度为 \(l\)，胸围为 \(C\)， 体积为 \(V\)， 质量为\(m\).

1. 将鱼视为类圆柱体，其高与底面周长同\(l\)、\(C\) 成正比例关系. 由底面周长与底面面积的平方关系，可以得到鱼体积

   \[\begin{equation} V = klC^2 \end{equation} \label{2.p.1} \]

   其中，\(k\) 是比例系数.

2. 假设池中所有成年鲈鱼的身体密度相同. 考虑到体积更小的幼年鲈鱼必定密度不同（通常更小），所以对于整个鲈鱼群体而言，\(m\) - \(V\) 不会成正比例关系. 因此，为了使成年鲈鱼的 \(m\) - \(V\) 关系模型更接近实际情况，我们加入一个常数 \(b\)，得到

   \[\begin{equation} m = \rho V + b \end{equation} \label{2.p.2} \]

模型建立与参数确定

将 \(\eqref{2.p.1}\)代入\(\eqref{2.p.2}\)，可以得到

\[m = k\rho lC^2+b =alC^2+b \]

其中，\(a=k\rho\)

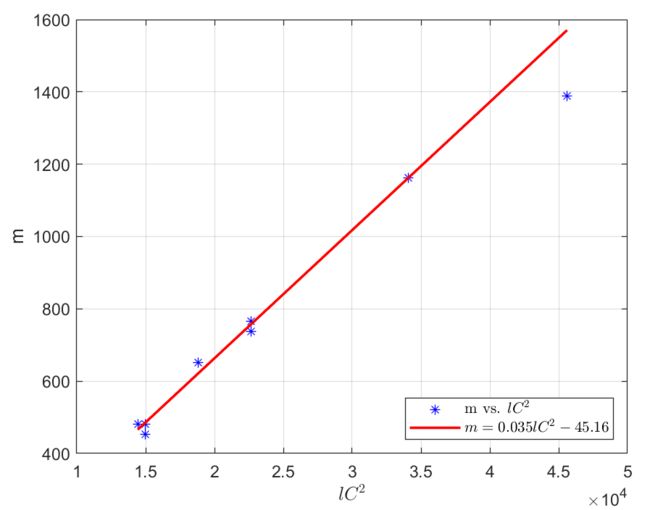
利用最小二乘法，根据所给数据拟合上式，得到

\[\begin{align} a&=0.035 &b=-45.16 \end{align} \]

即

\[m=0.035lC^2-45.16 \]

如下图所示

模型解释

1. 最终得到的常数 \(b=-45.16\)，说明成年鲈鱼的质量随体积的增长速度比幼年鲈鱼快，这与前文分析时猜测的“幼年鲈鱼身体密度更小”是相符的；
2. 拟合曲线在\(m=1389\) 的点误差较大，意味着“过大鲈鱼”可能会出现身体密度减小的情况；
3. 拟合曲线在大部分的点上误差很小，模型具有应用价值。