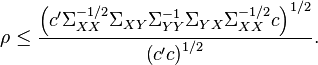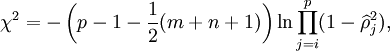典型相关分析相关资料

典型相关分析的基本思想 Canonical Correlation Analysis

 

CCA典型相关分析
（canonical correlation analysis）利用综合变量对之间的相关关系来反映两组指标之间的整体相关性的多元统计分析方法。它的基本原理是：为了从总体上把握两组指标之间的相关关系，分别在两组变量中提取有代表性的两个综合变量U1和V1（分别为两个变量组中各变量的线性组合），利用这两个综合变量之间的相关关系来反映两组指标之间的整体相关性。

 

Canonical Correlation Analysis典范相关分析/Canonical Correspondence Analysis典范对应分析

 

简单相关系数描述两组变量的相关关系的缺点:只是孤立考虑单个X与单个Y间的相关，没有考虑X、Y变量组内部各变量间的相关。两组间有许多简单相关系数，使问题显得复杂，难以从整体描述。典型相关是简单相关、多重相关的推广。典型相关是研究两组变量之间相关性的一种统计分析方法。也是一种降维技术。
1936年，Hotelling提出典型相关分析。考虑两组变量的线性组合, 并研究它们之间的相关系数p(u,v).在所有的线性组合中, 找一对相关系数最大的线性组合, 用这个组合的单相关系数来表示两组变量的相关性, 叫做两组变量的典型相关系数, 而这两个线性组合叫做一对典型变量。在两组多变量的情形下, 需要用若干对典型变量才能完全反映出它们之间的相关性。下一步, 再在两组变量的与u1,v1不相关的线性组合中, 找一对相关系数最大的线性组合, 它就是第二对典型变量, 而且p(u2,v2)就是第二个典型相关系数。这样下去, 可以得到若干对典型变量, 从而提取出两组变量间的全部信息。
典型相关分析的实质就是在两组随机变量中选取若干个有代表性的综合指标（变量的线性组合）, 用这些指标的相关关系来表示原来的两组变量的相关关系。这在两组变量的相关性分析中, 可以起到合理的简化变量的作用; 当典型相关系数足够大时, 可以像回归分析那样, 由- 组变量的数值预测另一组变量的线性组合的数值。

 

 

典型关联分析（Canonical Correlation Analysis）

[pdf版本] 典型相关分析.pdf

1. 问题

在线性回归中，我们使用直线来拟合样本点，寻找n维特征向量X和输出结果（或者叫做label）Y之间的线性关系。其中，。然而当Y也是多维时，或者说Y也有多个特征时，我们希望分析出X和Y的关系。

当然我们仍然可以使用回归的方法来分析，做法如下：

假设，，那么可以建立等式Y=AX如下

其中，形式和线性回归一样，需要训练m次得到m个。

这样做的一个缺点是，Y中的每个特征都与X的所有特征关联，Y中的特征之间没有什么联系。

我们想换一种思路来看这个问题，如果将X和Y都看成整体，考察这两个整体之间的关系。我们将整体表示成X和Y各自特征间的线性组合，也就是考察和之间的关系。

这样的应用其实很多，举个简单的例子。我们想考察一个人解题能力X（解题速度，解题正确率）与他/她的阅读能力Y（阅读速度，理解程度）之间的关系，那么形式化为：

和

然后使用Pearson相关系数

来度量u和v的关系，我们期望寻求一组最优的解a和b，使得Corr(u, v)最大，这样得到的a和b就是使得u和v就有最大关联的权重。

到这里，基本上介绍了典型相关分析的目的。

2. CCA表示与求解

给定两组向量和（替换之前的x为，y为），维度为，维度为，默认。形式化表示如下：

是x的协方差矩阵；左上角是自己的协方差矩阵；右上角是；左下角是，也是的转置；右下角是的协方差矩阵。

与之前一样，我们从和的整体入手，定义

我们可以算出u和v的方差和协方差：

上面的结果其实很好算，推导一下第一个吧：

最后，我们需要算Corr(u,v)了

我们期望Corr(u,v)越大越好，关于Pearson相关系数，《数据挖掘导论》给出了一个很好的图来说明：

横轴是u，纵轴是v，这里我们期望通过调整a和b使得u和v的关系越像最后一个图越好。其实第一个图和最后一个图有联系的，我们可以调整a和b的符号，使得从第一个图变为最后一个。

接下来我们求解a和b。

回想在LDA中，也得到了类似Corr(u,v)的公式，我们在求解时固定了分母，来求分子（避免a和b同时扩大n倍仍然符号解条件的情况出现）。这里我们同样这么做。

这个优化问题的条件是：

Maximize Subject to:

求解方法是构造Lagrangian等式，这里我简单推导如下：

求导，得

令导数为0后，得到方程组：

第一个等式左乘，第二个左乘，再根据，得到

也就是说求出的即是Corr(u,v)，只需找最大即可。

让我们把上面的方程组进一步简化，并写成矩阵形式，得到

写成矩阵形式

令

那么上式可以写作：

显然，又回到了求特征值的老路上了，只要求得的最大特征值，那么Corr(u,v)和a和b都可以求出。

在上面的推导过程中，我们假设了和均可逆。一般情况下都是可逆的，只有存在特征间线性相关时会出现不可逆的情况，在本文最后会提到不可逆的处理办法。

再次审视一下，如果直接去计算的特征值，复杂度有点高。我们将第二个式子代入第一个，得

这样先对求特征值和特征向量，然后根据第二个式子求得b。

待会举个例子说明求解过程。

假设按照上述过程，得到了最大时的和。那么和称为典型变量（canonical variates），即是u和v的相关系数。

最后，我们得到u和v的等式为：

我们也可以接着去寻找第二组典型变量对，其最优化条件是

Maximize Subject to:

其实第二组约束条件就是。

计算步骤同第一组计算方法，只不过是取的第二大特征值。

得到的和其实也满足

即

总结一下，i和j分别表示和得到结果

3. CCA计算例子

我们回到之前的评价一个人解题和其阅读能力的关系的例子。假设我们通过对样本计算协方差矩阵得到如下结果：

然后求，得

这里的A和前面的中的A不是一回事（这里符号有点乱，不好意思）。

然后对A求特征值和特征向量，得到

然后求b，之前我们说的方法是根据求b，这里，我们也可以采用类似求a的方法来求b。

回想之前的等式

我们将上面的式子代入下面的，得

然后直接对求特征向量即可，注意和的特征值相同，这个可以自己证明下。

不管使用哪种方法，

这里我们得到a和b的两组向量，到这还没完，我们需要让它们满足之前的约束条件

这里的应该是我们之前得到的VecA中的列向量的m倍，我们只需要求得m，然后将VecA中的列向量乘以m即可。

这里的是VecA的列向量。

因此最后的a和b为：

第一组典型变量为

相关系数

第二组典型变量为

相关系数

这里的（解题速度），（解题正确率），（阅读速度），（阅读理解程度）。他们前面的系数意思不是特征对单个u或v的贡献比重，而是从u和v整体关系看，当两者关系最密切时，特征计算时的权重。

4. Kernel Canonical Correlation Analysis（KCCA）

通常当我们发现特征的线性组合效果不够好或者两组集合关系是非线性的时候，我们会尝试核函数方法，这里我们继续介绍Kernel CCA。

在《支持向量机-核函数》那一篇中，大致介绍了一下核函数，这里再简单提一下：

当我们对两个向量作内积的时候

我们可以使用，来替代和，比如原来的特征向量为，那么

我们可以定义

如果与的构造一样，那么

这样，仅通过计算x和y的内积的平方就可以达到在高维空间（这里为）中计算和内积的效果。

由核函数，我们可以得到核矩阵K，其中

即第行第列的元素是第个和第个样例在核函数下的内积。

一个很好的核函数定义：

其中样例x有n个特征，经过变换后，从n维特征上升到了N维特征，其中每一个特征是。

回到CCA，我们在使用核函数之前

这里假设x和y都是n维的，引入核函数后，和变为了N维。

使用核函数后，u和v的公式为：

这里的c和d都是N维向量。

现在我们有样本，这里的表示样本x的第i个样例，是n维向量。

根据前面说过的相关系数，构造拉格朗日公式如下：

其中

然后让L对a求导，令导数等于0，得到（这一步我没有验证，待会从宏观上解释一下）

同样对b求导，令导数等于0，得到

求出c和d干嘛呢？c和d只是的系数而已，按照原始的CCA做法去做就行了呗，为了再引入和？

回答这个问题要从核函数的意义上来说明。核函数初衷是希望在式子中有，然后用K替换之，根本没有打算去计算出实际的。因此即是按照原始CCA的方式计算出了c和d，也是没用的，因为根本有没有实际的让我们去做。另一个原因是核函数比如高斯径向基核函数可以上升到无限维，N是无穷的，因此c和d也是无穷维的，根本没办法直接计算出来。我们的思路是在原始的空间中构造出权重和，然后利用将和上升到高维，他们在高维对应的权重就是c和d。

虽然和是在原始空间中（维度为样例个数M），但其作用点不是在原始特征上，而是原始样例上。看上面得出的c和d的公式就知道。通过控制每个高维样例的权重，来控制c。

好了，接下来我们看看使用和后，u和v的变化

表示可以将第i个样例上升到的N维向量，意义可以类比原始CCA的x。

鉴于这样表示接下来会越来越复杂，改用矩阵形式表示。

简写为

其中X（M×N）为

我们发现

我们可以算出u和v的方差和协方差（这里实际上事先对样本和做了均值归0处理）：

这里和维度可以不一样。

最后，我们得到Corr(u,v)

可以看到，在将和处理成，后，得到的结果和之前形式基本一样，只是将替换成了两个K乘积。

因此，得到的结果也是一样的，之前是

其中

引入核函数后，得到

其中

注意这里的两个w有点区别，前面的维度和x的特征数相同，维度和y的特征数相同。后面的维度和x的样例数相同，维度和y的样例数相同，严格来说“维度=维度”。

5. 其他话题

1、当协方差矩阵不可逆时，怎么办？

要进行regularization。

一种方法是将前面的KCCA中的拉格朗日等式加上二次正则化项，即：

这样求导后得到的等式中，等式右边的矩阵一定是正定矩阵。

第二种方法是在Pearson系数的分母上加入正则化项，同样结果也一定可逆。

2、求Kernel矩阵效率不高怎么办？

使用Cholesky decomposition压缩法或者部分Gram-Schmidt正交化法，。

3、怎么使用CCA用来做预测？

　　

4、如果有多个集合怎么办？X、Y、Z…？怎么衡量多个样本集的关系？

这个称为Generalization of the Canonical Correlation。方法是使得两两集合的距离差之和最小。可以参考文献2。

6. 参考文献

1、 http://www.stat.tamu.edu/~rrhocking/stat636/LEC-9.636.pdf

2、 Canonical correlation analysis: An overview with application to learning methods. David R. Hardoon , Sandor Szedmak and John Shawe-Taylor

3、 A kernel method for canonical correlation analysis. Shotaro Akaho

4、 Canonical Correlation a Tutorial. Magnus Borga

5、 Kernel Canonical Correlation Analysis. Max Welling

http://www.cnblogs.com/jerrylead/archive/2011/06/20/2085491.html Canonical correlation

From Wikipedia, the free encyclopedia

Jump to: navigation , search

In statistics, canonical correlation analysis, introduced by Harold Hotelling, is a way of making sense of cross-covariance matrices. If we have two sets of variables, and , and there are correlations among the variables, then canonical correlation analysis will enable us to find linear combinations of the 's and the 's which have maximum correlation with each other.

Contents [hide] 1 Definition 2 Computation 2.1 Proof 2.2 Solution 3 Hypothesis testing 4 Practical uses 5 Connection to principal angles 6 See also 7 Notes 8 References 9 External links

[edit] Definition

Given two column vectors and of random variables with finite second moments, one may define the cross-covariance to be the matrix whose entry is the covariance . In practice, we would estimate the covariance matrix based on sampled data from and (i.e. from a pair of data matrices).

Canonical correlation analysis seeks vectors and such that the random variables and maximize the correlation . The random variables and are the first pair of canonical variables. Then one seeks vectors maximizing the same correlation subject to the constraint that they are to be uncorrelated with the first pair of canonical variables; this gives the second pair of canonical variables. This procedure may be continued up to times.

[edit] Computation

[edit] Proof

Let and . The parameter to maximize is

The first step is to define a change of basis and define

And thus we have

By the Cauchy-Schwarz inequality, we have

There is equality if the vectors and are collinear. In addition, the maximum of correlation is attained if is the eigenvector with the maximum eigenvalue for the matrix (see Rayleigh quotient). The subsequent pairs are found by using eigenvalues of decreasing magnitudes. Orthogonality is guaranteed by the symmetry of the correlation matrices.

[edit] Solution

The solution is therefore:

• is an eigenvector of
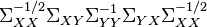
• is proportional to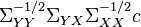

Reciprocally, there is also:

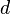• is an eigenvector of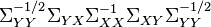
• is proportional to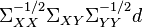

Reversing the change of coordinates, we have that

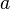• is an eigenvector of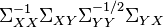
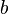• is an eigenvector of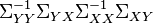
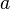• is proportional to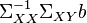
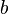• is proportional to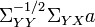

The canonical variables are defined by:

[edit] Hypothesis testing

Each row can be tested for significance with the following method. Since the correlations are sorted, saying that row is zero implies all further correlations are also zero. If we have independent observations in a sample and is the estimated correlation for . For the th row, the test statistic is:

which is asymptotically distributed as a chi-squared with degrees of freedom for large .^[1] Since all the correlations from to are logically zero (and estimated that way also) the product for the terms after this point is irrelevant.

[edit] Practical uses

A typical use for canonical correlation in the experimental context is to take two sets of variables and see what is common amongst the two sets. For example in psychological testing, you could take two well established multidimensional personality tests such as the Minnesota Multiphasic Personality Inventory (MMPI) and the NEO. By seeing how the MMPI factors relate to the NEO factors, you could gain insight into what dimensions were common between the tests and how much variance was shared. For example you might find that an extraversion or neuroticism dimension accounted for a substantial amount of shared variance between the two tests.

One can also use canonical correlation analysis to produce a model equation which relates two sets of variables, for example a set of performance measures and a set of explanatory variables, or a set of outputs and set of inputs. Constraint restrictions can be imposed on such a model to ensure it reflects theoretical requirements or intuitively obvious conditions. This type of model is known as a maximum correlation model.^[2]

Visualization of the results of canonical correlation is usually through bar plots of the coefficients of the two sets of variables for the pairs of canonical variates showing significant correlation. Some authors suggest that they are best visualized by plotting them as heliographs, a circular format with ray like bars, with each half representing the two sets of variables.^[3]

[edit] Connection to principal angles

Assuming that and have zero expected values, i.e., , their covariance matrices and can be viewed as Gram matrices in an inner product, see Covariance#Relationship_to_inner_products, for the columns of and , correspondingly. The definition of the canonical variables and is equivalent to the definition of principal vectors for the pair of subspaces spanned by the columns of and with respect to this inner product. The canonical correlations is equal to the cosine of principal angles.

[edit] See also

• Regularized canonical correlation analysis
• Generalized Canonical Correlation
• RV coefficient
• Principal angles

 

Canonical Correlation Analysis

Canonical correlation analysis (CCA) is a way of measuring the linear relationship between two multidimensional variables. It finds two bases, one for each variable, that are optimal with respect to correlations and, at the same time, it finds the corresponding correlations. In other words, it finds the two bases in which the correlation matrix between the variables is diagonal and the correlations on the diagonal are maximized. The dimensionality of these new bases is equal to or less than the smallest dimensionality of the two variables.

For more information on CCA, please read my on-line tutorial (or the PDF version).

Matlab functions

• cca.m CCA

• ccabss.m Blind Source Separation based on CCA. For reference, see A Canonical Correlation Approach to Exploratory Data Analysis in fMRI.

Please email your comments to me.

 

 

 

Canonical Correspondence Analysis

Description

Performs a Canonical Correspondence Analysis.

Usage

cca(sitspe, sitenv, scannf = TRUE, nf = 2)  

Arguments

sitspe	a data frame for correspondence analysis, typically a sites x species table
sitenv	a data frame containing variables, typically a sites x environmental variables table
scannf	a logical value indicating whether the eigenvalues bar plot should be displayed
nf	if scannf FALSE, an integer indicating the number of kept axes

Value

returns an object of class pcaiv. See pcaiv

Author(s)

Daniel Chessel
Anne B Dufour [email protected]

References

Ter Braak, C. J. F. (1986) Canonical correspondence analysis : a new eigenvector technique for multivariate direct gradient analysis. Ecology, 67, 1167–1179.

Ter Braak, C. J. F. (1987) The analysis of vegetation-environment relationships by canonical correspondence analysis. Vegetatio, 69, 69–77.

Chessel, D., Lebreton J. D. and Yoccoz N. (1987) Propriétés de l'analyse canonique des correspondances. Une utilisation en hydrobiologie. Revue de Statistique Appliquée, 35, 55–72.

See Also

cca in the package vegan

Examples

data(rpjdl) millog <- log(rpjdl$mil + 1) iv1 <- cca(rpjdl$fau, millog, scan = FALSE) plot(iv1) # analysis with c1 - as - li -ls # projections of inertia axes on PCAIV axes s.corcircle(iv1$as) # Species positions s.label(iv1$c1, 2, 1, clab = 0.5, xlim = c(-4,4)) # Sites positions at the weighted mean of present species s.label(iv1$ls, 2, 1, clab = 0, cpoi = 1, add.p = TRUE) # Prediction of the positions by regression on environmental variables s.match(iv1$ls, iv1$li, 2, 1, clab = 0.5) # analysis with fa - l1 - co -cor # canonical weights giving unit variance combinations s.arrow(iv1$fa) # sites position by environmental variables combinations # position of species by averaging s.label(iv1$l1, 2, 1, clab = 0, cpoi = 1.5) s.label(iv1$co, 2, 1, add.plot = TRUE) s.distri(iv1$l1, rpjdl$fau, 2, 1, cell = 0, csta = 0.33) s.label(iv1$co, 2, 1, clab = 0.75, add.plot = TRUE) # coherence between weights and correlations par(mfrow = c(1,2)) s.corcircle(iv1$cor, 2, 1) s.arrow(iv1$fa, 2, 1) par(mfrow = c(1,1))  

Worked out examples

> library(ade4) > ### Name: cca > ### Title: Canonical Correspondence Analysis > ### Aliases: cca > ### Keywords: multivariate > > ### ** Examples > > data(rpjdl) > millog <- log(rpjdl$mil + 1) > iv1 <- cca(rpjdl$fau, millog, scan = FALSE) > plot(iv1)  

> > # analysis with c1 - as - li -ls > # projections of inertia axes on PCAIV axes > s.corcircle(iv1$as)  

> > # Species positions > s.label(iv1$c1, 2, 1, clab = 0.5, xlim = c(-4,4)) > # Sites positions at the weighted mean of present species > s.label(iv1$ls, 2, 1, clab = 0, cpoi = 1, add.p = TRUE)  

> > # Prediction of the positions by regression on environmental variables > s.match(iv1$ls, iv1$li, 2, 1, clab = 0.5)  

> > # analysis with fa - l1 - co -cor > # canonical weights giving unit variance combinations > s.arrow(iv1$fa)  

> > # sites position by environmental variables combinations > # position of species by averaging > s.label(iv1$l1, 2, 1, clab = 0, cpoi = 1.5)  

> s.label(iv1$co, 2, 1, add.plot = TRUE)  

> > s.distri(iv1$l1, rpjdl$fau, 2, 1, cell = 0, csta = 0.33)  

> s.label(iv1$co, 2, 1, clab = 0.75, add.plot = TRUE)  

> > # coherence between weights and correlations > par(mfrow = c(1,2)) > s.corcircle(iv1$cor, 2, 1)  

> s.arrow(iv1$fa, 2, 1)  

> par(mfrow = c(1,1)) 

（一）CCA方法简介：
 典范对应分析（canonical correspondence analusis, CCA），是基于对应分析发展而来的一种排序方法，将对应分析与多元回归分析相结合，每一步计算均与环境因子进行回归，又称多元直接梯度分析。其基本思路是在对应分析的迭代过程中，每次得到的样方排序坐标值均与环境因子进行多元线性回归。CCA要求两个数据矩阵，一个是植被数据矩阵，一个是环境数据矩阵。首先计算出一组样方排序值和种类排序值（同对应分析），然后将样方排序值与环境因子用回归分析方法结合起来，这样得到的样方排序值即反映了样方种类组成及生态重要值对群落的作用，同时也反映了环境因子的影响，再用样方排序值加权平均求种类排序值，使种类排序坐标值值也简介地与环境因子相联系。其算法可由Canoco软件快速实现。
 最大优点：CCA是一种基于单峰模型的排序方法，样方排序与对象排序对应分析，而且在排序过程中结合多个环境因子，因此可以把样方、对象与环境因子的排序结果表示在同一排序图上。
 缺点：存在“弓形效应”。克服弓形效应可以采用除趋势典范对应分析（detrended canonical correspondence, DCCA）.
 结果可信性：查看累计贡献率及环境与研究对象前两个排序轴之间的相关性。
（二）CCA排序图解释：箭头表示环境因子，箭头所处的象限表示环境因子与排序轴之间的正负相关性，箭头连线的长度代表着某个环境因子与研究对象分布相关程度的大小，连线越长，代表这个环境因子对研究对象的分布影响越大。箭头连线与排序轴的家教代表这某个环境因子与排序轴的相关性大小，夹角越小，相关性越高。
（三）关键问题：
 （1）RDA或CCA的选择问题：RDA是基于线性模型，CCA是基于单峰模型。一般我们会选择CCA来做直接梯度分析。但是如果CCA排序的效果不太好，就可以考虑是不是用RDA分析。RDA或CCA选择原则：先用species-sample资料做DCA分析，看分析结果中Lengths of gradient 的第一轴的大小，如果大于4.0，就应该选CCA，如果3.0-4.0之间，选RDA和CCA均可，如果小于3.0, RDA的结果要好于CCA。
 （2）计算单个环境因子的贡献率：CCA分析里面所得到的累计贡献率是所有环境因子的贡献率，怎么得到每个环境因子的贡献率：生成三个矩阵，第一个是物种样方矩阵，第二个是目标环境因子矩阵，第三个是剔除目标环境因子矩阵后的环境因子矩阵。分别输入Canoco软件中，这样CCA分析得到的特征根贡献率即是单个目标环境因子的贡献率。
参考书目：
张金屯 数量生态学 科学出版社 2004
Jan Leps & Peter Smilauer. Multivariate analysis of ecological data using CANOCO. Cambridge University Press. 2003
 
 
 
本文引用地址：http://www.sciencenet.cn/blog/user_content.aspx?id=27852
 
 典范对应分析（CCA）
 （一）CCA方法简介：
 典范对应分析（canonical correspondence analusis, CCA），是基于对应分析发展而来的一种排序方法，将对应分析与多元回归分析相结合，每一步计算均与环境因子进行回归，又称多元直接梯度分析。其基本思路是在对应分析的迭代过程中，每次得到的样方排序坐标值均与环境因子进行多元线性回归。CCA要求两个数据矩阵，一个是植被数据矩阵，一个是环境数据矩阵。 首先计算出一组样方排序值和种类排序值（同对应分析），然后将样方排序值与环境因子用回归分析方法结合起来，这样得到的样方排序值即反映了样方种类组成及生态重要值对群落的作用，同时也反映了环境因子的影响，再用样方排序值加权平均求种类排序值，使种类排序坐标值值也简介地与环境因子相联系。其算法可由Canoco软件快速实现。
 最大优点：CCA是一种基于单峰模型的排序方法，样方排序与对象排序对应分析，而且在排序过程中结合多个环境因子，因此可以把样方、对象与环境因子的排序结果表示在同一排序图上。
 缺点：存在“弓形效应”。克服弓形效应可以采用除趋势典范对应分析（detrended canonical correspondence, DCCA）.
 结果可信性：查看累计贡献率及环境与研究对象前两个排序轴之间的相关性。
 （二）CCA排序图解释
 箭头表示环境因子，箭头所处的象限表示环境因子与排序轴之间的正负相关性，箭头连线的长度代表着某个环境因子与研究对象分布相关程度的大小，连线越长，代表这个环境因子对研究对象的分布影响越大。箭头连线与排序轴的家教代表这某个环境因子与排序轴的相关性大小，夹角越小，相关性越高。
 （三）关键问题：
 （1）RDA或CCA的选择问题：RDA是基于线性模型，CCA是基于单峰模型。一般我们会选择CCA来做直接梯度分析。但是如果CCA排序的效果不太好，就可以考虑是不是用RDA分析。RDA或CCA选择原则：先用species-sample资料做DCA分析，看分析结果中Lengths of gradient 的第一轴的大小，如果大于4.0，就应该选CCA，如果3.0-4.0之间，选RDA和CCA均可，如果小于3.0, RDA的结果要好于CCA。
 （2）计算单个环境因子的贡献率：CCA分析里面所得到的累计贡献率是所有环境因子的贡献率，怎么得到每个环境因子的贡献率：生成三个矩阵，第一个是物种样方矩阵，第二个是目标环境因子矩阵，第三个是剔除目标环境因子矩阵后的环境因子矩阵。分别输入Canoco软件中，这样CCA分析得到的特征根贡献率即是单个目标环境因子的贡献率。
 
    

典型相关分析 Canonical Correlation Analysis(CCA)

• 两个随机变量Y与X 简单相关系数
• 一个随机变量Y与一组随机变量X1，X2……，Xp 多重相关（复相关系数）
• 一组随机变量Y1，Y2，……，Yq与另一组随机变量X1，X2，……，Xp 典型相关系数
  

典型相关是研究两组变量之间相关性的一种统计分析方法。也是一种降维技术。

 
 
 

简单相关系数描述两组变量的相关关系的缺点：

• 只是孤立考虑单个X与单个Y间的相关，没有考虑X，Y变量组内部各变量间的相关。
• 两组间有许多简单相关系数（实例为30个），使问题显得复杂，难以从整体描述。（复相关系数也如此）