【预备操作】
以下方法请先安装和加载forecast/fpp包
install.packages("forecast") install.packages("fpp") library('forecast') library('fpp')
以下方法被笔者实用在自己论文实验中,相关论文发表在ICTAI 2013
Detecting Impolite Crawler by using Time Series Analysis.
Zhiqian Chen, Wenya Feng
25th International Conference on Tools and Artificial Intelligence
移动平均分解法
用经典的移动平均分解时序为季节性,趋势和不规则部分,使用加法或乘法季节部分。
(Decompose a time series into seasonal, trend and irregular components using moving averages. Deals with additive or multiplicative seasonal component.)
1 births <- scan("http://robjhyndman.com/tsdldata/data/nybirths.dat")
2 birthstimeseries <- ts(births, frequency=12, start=c(1946,1))
注意这里的frequency要和最小单周期长度匹配效果才好(待学习)
3 如需查看可以 birthstimeseries 或 plot.ts(birthstimeseries)
4 birthstimeseriescomponents <- decompose(birthstimeseries)
估计出的季节性、趋势的和不规则部分现在被存储在变量birthstimeseriescomponents$seasonal, birthstimeseriescomponents$trend 和 birthstimeseriescomponents$random
6 plot(birthstimeseriescomponents)

以下是去掉季节性的时序
7 birthstimeseriesseasonallyadjusted <- birthstimeseries - birthstimeseriescomponents$seasonal
8 plot(birthstimeseriesseasonallyadjusted)
或
7 birthstimeseriesadj <- seasadj(birthstimeseries)
8 plot(birthstimeseriesadj)
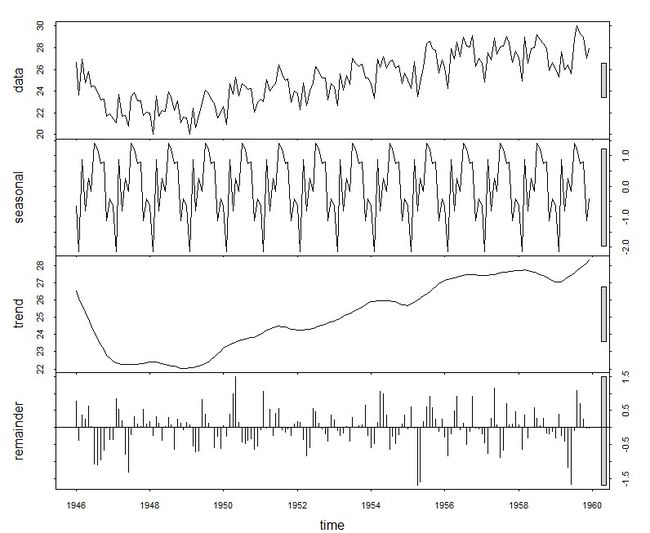
局部加权回归法
STL分解基于Loess,即局部加权回归散点平滑法,是1990年由密歇根大学的R. B. Cleveland教授以及AT&T Bell实验室的W. S. Cleveland等人提出来的一种对时间序列进行分解的方法。STL分解将时间序列分解成季节项、趋势项及残余项。
1 births <- scan("http://robjhyndman.com/tsdldata/data/nybirths.dat")
2 birthstimeseries <- ts(births, frequency=12, start=c(1946,1))
3 如需查看可以 birthstimeseries 或 plot.ts(birthstimeseries)
4 birthstimeseriescomponents <- stl(birthstimeseries,s.window="periodic")
5 plot(birthstimeseriescomponents)
6 birthstimeseriescomponents <- forecast(birthstimeseriescomponents)
7 plot(birthstimeseriescomponents)
笔者尝试用STL预测手头的一个时序数据(第一列是实际观察值(a),第二列是预测值(b),第三列是1-(b-a)/a的百分比格式数据),总体偏大5%-10%,还是不错的:
| 55701279 | 58251140 | 95.42% |
| 64829888 | 71947199 | 89.02% |
| 65720870 | 72256152 | 90.06% |
| 65596679 | 69039714 | 94.75% |
| 64781972 | 70811590 | 90.69% |
| 60384601 | 62627480 | 96.29% |
| 54116447 | 56363455 | 95.85% |
指数平滑法(HoltWinters)
如果你的时间序列可以被描述为一个增长或降低趋势的、没有季节性的相加模型,你可以使用霍尔特指数平滑法对其进行短期预测。Holt指数平滑法估计当前时间点的水平和斜率。其平滑化是由两个参数控制的,alpha,用于估计当前时间点的水平,beta,用于估计当前时间点趋势部分的斜率。正如简单指数平滑法一样,alpha和beta参数都介于0到1之间,并且当参数越接近0,大多数近期的观测则将占据预测更小的权重。
1 skirts <- scan("http://robjhyndman.com/tsdldata/roberts/skirts.dat",skip=5)
2 skirtsseries <- ts(skirts,start=c(1866))
3 plot.ts(skirtsseries)
4 skirtsseriesforecasts <- HoltWinters(skirtsseries, gamma=FALSE)
样本内预测,意义?
5 plot(skirtsseriesforecasts)
6 skirtsseriesforecasts2 <- forecast.HoltWinters(skirtsseriesforecasts, h=19)
7 plot.forecast(skirtsseriesforecasts2)
和简单指数平滑法一样,我们瞧瞧样本内预测误差是否在延迟1-20阶时是非零自相关的,以此来检验模型是否还
可以被优化。如裙边数据中,我们可以创建一个相关图,进行Ljung-Box检验
1 acf(skirtsseriesforecasts2$residuals, lag.max=20) 2 Box.test(skirtsseriesforecasts2$residuals, lag=20, type="Ljung-Box")
一般取20阶,而且统计量Q的P值>0.05则不能拒绝随机时序假设(就说无自相关性的随机了,时序无信息。概率越大越确定?),反之则使非白噪声序列。纯随机性检验,P值小于5%,序列为非白噪声
在拿不准情况下可以做正太直方图
自回归整合移动平均(ARIMA)
指数平滑法对于预测来说是非常有帮助的,而且它对时间序列上面连续的值之间相关性没有要求。但是,如果你想使用指数平滑法计算出预测区间,那么预测误差必须是不相关的,而且必须是服从零均值、方差不变的正态分布。 即使指数平滑法对时间序列连续数值之间相关性没有要求,在某种情况下,我们可以通过考虑数据之间的相关性来创建更好的预测模型。自回归移动平均模型(ARIMA)包含一个确定(explicit)的统计模型用于处理时间序列的不规则部分,它也允许不规则部分可以自相关。
1 volcanodust <- scan("http://robjhyndman.com/tsdldata/annual/dvi.dat", skip=1)
2 volcanodustseries <- ts(volcanodust,start=c(1500))
3 plot.ts(volcanodustseries)
4 auto.arima(volcanodust)
根据给出来的参数在下一步选择建模参数order(q,d,p)
5 volcanodustseriesarima <- arima(volcanodustseries, order=c(2,0,0))
6 volcanodustseriesforecasts <- forecast.Arima(volcanodustseriesarima, h=31)
7 plot.forecast(volcanodustseriesforecasts)
参考文献:
本文主要参考, http://a-little-book-of-r-for-time-series.readthedocs.org/en/latest/src/timeseries.html
某sina网友对STL方法的理解,http://blog.sina.com.cn/s/blog_5ffd41cf01012i5e.html
STL方法发源论文, http://cs.wellesley.edu/~cs315/Papers/stl%20statistical%20model.pdf
fpp使用理论和具体方法, http://otexts.com/fpp/
robjhyndman教授网站, http://robjhyndman.com/?s=seasadj
robjhyndman教授的课件, http://maths-people.anu.edu.au/~johnm/courses/r/ASC2008/pdf/Rtimeseries-ohp.pdf