算法设计与分析: 5-15 智力拼图问题

5-15 智力拼图问题

---

问题描述

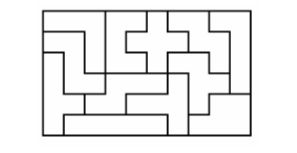
设有 12 个平面图形如图所示。每个图形的形状互不相同，但它们都是由 5 个大小相同的正方形组成。下图中 12 个图形拼接成一个 6×10 的矩形。试设计一个算法，计算出用这 12 个图形拼接成给定矩形的拼接方案。

对于给定矩形，计算用上述 12 个图形拼接成给定矩形的一个拼接方案。拼接方案中每个图形可以经过旋转或翻转后进行拼接，但要求使用 12 个图形中每个图形恰好 1 次。

数据输入：
第一行有 2 个正整数 m 和 n，表示给定的矩形是一个 m×n m × n 矩形。

结果输出：
每行 n 个字符，共 m 行。给定的 12 个图形的编号如下。如果不存在所要求的拼接方案，输出“No solution!”。

---

Java

package Chapter5HuiSuFa;

import java.util.Arrays;
import java.util.Scanner;

public class ZhiLiPingTu {

    private static class pp{
        char[][] aa = new char[5][5];
    }

    private static class fboard{
        char[] pos = new char[60];
        char[] mark = new char[12];
    }

    private static char[][] pc00 = {{1,1,1,0,0},{1,0,0,0,0},{1,0,0,0,0},{0,0,0,0,0},{0,0,0,0,0}};
    private static char[][] pc01 = {{2,2,0,0,0},{2,0,0,0,0},{2,2,0,0,0},{0,0,0,0,0},{0,0,0,0,0}};
    private static char[][] pc02 = {{3,3,0,0,0},{3,3,0,0,0},{3,0,0,0,0},{0,0,0,0,0},{0,0,0,0,0}};
    private static char[][] pc03 = {{4,4,0,0,0},{4,0,0,0,0},{4,0,0,0,0},{4,0,0,0,0},{0,0,0,0,0}};
    private static char[][] pc04 = {{5,0,0,0,0},{5,5,0,0,0},{0,5,0,0,0},{0,5,0,0,0},{0,0,0,0,0}};
    private static char[][] pc05 = {{6,0,0,0,0},{6,6,0,0,0},{6,0,0,0,0},{6,0,0,0,0},{0,0,0,0,0}};
    private static char[][] pc06 = {{7,7,7,0,0},{0,7,0,0,0},{0,7,0,0,0},{0,0,0,0,0},{0,0,0,0,0}};
    private static char[][] pc07 = {{0,8,0,0,0},{8,8,8,0,0},{0,8,0,0,0},{0,0,0,0,0},{0,0,0,0,0}};
    private static char[][] pc08 = {{0,9,0,0,0},{9,9,0,0,0},{0,9,9,0,0},{0,0,0,0,0},{0,0,0,0,0}};
    private static char[][] pc09 = {{10,10,10,10,10},{0,0,0,0,0},{0,0,0,0,0},{0,0,0,0,0},{0,0,0,0,0}};
    private static char[][] pc10 = {{0,11,11,0,0},{11,11,0,0,0},{11,0,0,0,0},{0,0,0,0,0},{0,0,0,0,0}};
    private static char[][] pc11 = {{12,12,0,0,0},{0,12,0,0,0},{0,12,12,0,0},{0,0,0,0,0},{0,0,0,0,0}};

    private static pp[] orig;

    private static int brow,bcol;
    private static pp[][] var = new pp[12][8];
    private static int[] nvar = new int[12];

    private static boolean flg;
    private static int ans;

    public static void main(String[] args){
        Scanner input = new Scanner(System.in);

        while (true){
            ans = 0;

            brow = input.nextInt();
            bcol = input.nextInt();

            if(brow < bcol){
                int tmp = brow;
                brow = bcol;
                bcol = tmp;
                flg = true;
            }
            if(bcol<3 || brow*bcol!=60)
                System.out.println("No Solution!");
            else{
                init();
                fboard ff = new fboard();
                search(ff);
            }
        }
    }

    private static void init(){
        initOrig();
        pp tmp1 = new pp();
        pp tmp2 = new pp();
        for(int b=0; b<12; b++){
            copyPP(orig[b],tmp1);
            for(int d=0; d<5; d++)
                for(int c=0; c<5; c++)
                    if(tmp1.aa[d][c] > 0)
                        tmp1.aa[d][c] |= 0x10;
            int vc=0;
            for(int a=0; a<8; a++){
                boolean exist = false;
                for(int c=0; cif(Arrays.deepEquals(var[b][c].aa,tmp1.aa))
                        exist = true;
                if(!exist){
                    pp tmp = new pp();
                    copyPP(tmp1,tmp);
                    var[b][vc++] = tmp;
                }

                //旋转
                copyPP(tmp1,tmp2);
                rotp(tmp1,tmp2);
                //翻转
                if(a == 3){
                    copyPP(tmp1,tmp2);
                    flip(tmp1,tmp2);
                }
            }
            nvar[b] = vc;
        }
    }

    private static void copyPP(pp src, pp des){
        char[][] aa = new char[5][5];
        for(int i=0; i<5; i++)
            aa[i] = Arrays.copyOf(src.aa[i],5);

        des.aa = aa;
    }

    private static void initOrig(){
        orig = new pp[12];
        orig[0] = new pp();
        orig[1] = new pp();
        orig[2] = new pp();
        orig[3] = new pp();
        orig[4] = new pp();
        orig[5] = new pp();
        orig[6] = new pp();
        orig[7] = new pp();
        orig[8] = new pp();
        orig[9] = new pp();
        orig[10] = new pp();
        orig[11] = new pp();

        orig[0].aa = pc00;
        orig[1].aa = pc01;
        orig[2].aa = pc02;
        orig[3].aa = pc03;
        orig[4].aa = pc04;
        orig[5].aa = pc05;
        orig[6].aa = pc06;
        orig[7].aa = pc07;
        orig[8].aa = pc08;
        orig[9].aa = pc09;
        orig[10].aa = pc10;
        orig[11].aa = pc11;
    }

    private static void rotp(pp des, pp src){
        clearPP(des);
        boolean flag = false;
        for(int x=4,xp=0; x>=0; x--){
            for(int y=0; y<5; y++){
                des.aa[xp][y] = src.aa[y][x];
                if(src.aa[y][x] > 0)
                    flag = true;
            }
            if(flag) xp++;
        }
    }

    private static void clearPP(pp des){
        for(int i=0; i<5; i++)
            for(int j=0; j<5; j++)
                des.aa[i][j] = 0;
    }

    private static void flip(pp des, pp src){
        clearPP(des);
        boolean flag = false;
        for(int x=4,xp=0; x>=0; x--){
            for(int y=0; y<5; y++){
                des.aa[y][xp] = src.aa[y][x];
                if(src.aa[y][x] > 0)
                    flag = true;
            }
            if(flag) xp++;
        }
    }

    private static void search(fboard pre){
        int npla=0,frow=0,fcol=0;
        fboard ff = new fboard();
        char[] pos;
        char[] mark;
        pos = Arrays.copyOf(pre.pos,60);
        mark = Arrays.copyOf(pre.mark,12);
        ff.pos = pos;
        ff.mark = mark;
        if(ans > 0) return;
        //找最左上的未覆盖方格
        boolean found = false;
        for(int row=1; row<=brow && !found; row++)
            for(int col=1; col<=bcol && !found; col++)
                if(pre.pos[addr(row,col)] == 0){
                    frow = row;
                    fcol = col;
                    found = true;
                }
        //计算已用过的图形数
        for(int pn=0; pn<12; pn++)
            if(pre.mark[pn] > 0)
                npla++;
        for(int pn=0; pn<12; pn++){
            //是否已用过
            if(pre.mark[pn] > 0)
                continue;
            //对每种不同形态
            for(int pv=0; pvint py = frow;
                for(int px=1; px<=bcol; px++){
                    if(px > fcol) break;
                    if(check(tryp,ff,px,py)){
                        //用该图形覆盖
                        for(int row=0; row<5; row++){
                            for(int col=0; col<5; col++){
                                if(tryp.aa[row][col] > 0){
                                    ff.pos[addr(row+py,col+px)] |= tryp.aa[row][col];
                                }
                            }
                        }
                        ff.mark[pn] = 1;
                        if(npla > 10){
                            ++ans;
                            outf(ff);
                            return;
                        }else search(ff);
                        //回溯
                        pos = Arrays.copyOf(pre.pos,60);
                        mark = Arrays.copyOf(pre.mark,12);
                        ff.pos = pos;
                        ff.mark = mark;
                    }
                }
            }
        }
    }

    private static boolean check(pp tryp, fboard ff, int px, int py){
        for(int row=0; row<5; row++)
            for(int col=0; col<5; col++)
                if(tryp.aa[row][col] > 0){
                    int r=row+py,c=col+px;
                    if(r>brow || c>bcol || ff.pos[addr(r,c)]>0)
                        return false;
                }
        return true;
    }

    private static void outf(fboard ff){
        if(flg){
            for(int col=1; col<=bcol; col++){
                for(int row=1; row<=brow; row++){
                    int x = ff.pos[addr(row,col)]-16;
                    if(x < 10) System.out.print(x);
                    if(x == 10) System.out.print("a");
                    if(x == 11) System.out.print("b");
                    if(x == 12) System.out.print("c");
                }
                System.out.println();
            }
        }else {
            for(int row=1; row<=brow; row++){
                for(int col=1; col<=bcol; col++){
                    int x = ff.pos[addr(row,col)]-16;
                    if(x < 10) System.out.print(x);
                    if(x == 10) System.out.print("a");
                    if(x == 11) System.out.print("b");
                    if(x == 12) System.out.print("c");
                }
                System.out.println();
            }
        }
    }

    private static int addr(int row, int col){
        return (row-1)*bcol+col-1;
    }
}

Input & Output

6 10
111c9aaaaa
1ccc999777
1c3339bb74
22233bb874
26255b8884
6666555844

4 15
111bb6666777844
1555bb69cc78884
13355b999c72824
333aaaaa9cc2224

12 5
1115559aaaaa
1755cc99333b
1777c99833bb
272cc6888bb4
222666684444

---

Reference

王晓东《计算机算法设计与分析》